Adventures with Impossible Figures
1.Tri-bar
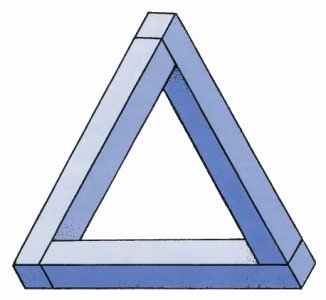
Let us make the acquaintance of our first impossible figure. What is it and what qualities does it have? We can see that this curious shape is made up of three bars, so for convenience let us call it a 'tri-bar'. What is a tri-bar?
To answer ŗ question like that we have to deal with two separate layers of illusion. All we are really looking at is ŗ set of lines printed on a piece of paper! Yet we appear to see a solid object. This first layer of illusion is sÓ familiar that we may even hesitate to regard it as an illusion at all. Yet that is what it is.
Once we accept that first layer of illusion then it is plain that there is still a second layer to understand. What is this curious tri-bar?
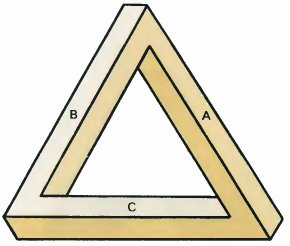
If we look carefully at the drawing, we can see that at the top corner, the bars A and B appear to be perpendicular. On the left, B and C are perpendicular. On the right — and ņ are perpendicular. How can this be?
The usual way to deal with a mysterious object is to try to understand it by examining it from different directions. This need not be done physically, it can be done in the imagination. If we see a box, a pencil or a teacup. then we can easily imagine how they would look from other directions without moving or touching them. An artist is perfectly able to sketch an object from one point of view while looking from another.
Can we do this with a tri-bar? What happens if we rotate it?
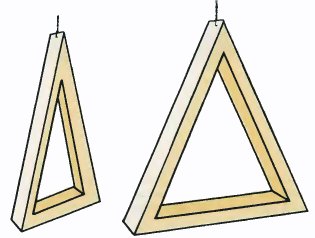
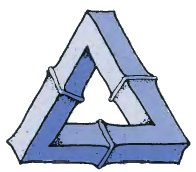
Are these two drawings views of a tri-bar as it rotates? Well, yes and no! Both at the same time! These drawings appear to represent nothing more than an ordinary triangular frame. The bars are no longer perpendicular and there would be no problem in making it out of wood or cardboard. At what point did the image disappear? Try to exercise your imagination by rotating the figure at the top of the page. What happens?
Here is a real photograph of an impossible tri-bar. No trickery. It is a real photograph. Surely that proves that you can make an impossible tri-bar?

The complete photograph below shows that it is indeed possible to make an object from pieces of wood which when viewed from a certain angle appears to be an impossible tri-bar. The position of the camera is vital. To show how it is done, we have placed a mirror behind. In the mirror it is clearly seen not to be an impossible tri-bar at all.

The impossible tri-bar is indeed a strange and curious object, and one which we must investigate further.
The Eye
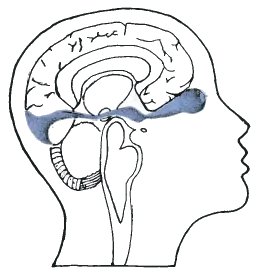
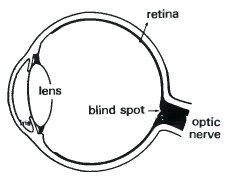
The organ which we call the eye is essentially a ball-shaped mini-camera. The lens focuses the image on the region at the back of the eye called the retina. This is made up of more than a hundred million light sensitive cells. From these cells more than a million nerve filaments carry the signals to the brain. These nerve filaments are bundled together as they leave the eye to make what is known as the optic nerve.
The signals transmitted along the optic nerve are processed in a specific part of the brain. This process is extremely complicated and barely understood, in spite of all the progress which has been made in recent years. However, for the purposes of this book, there is no need to be able to differentiate between the component parts. We shall call the whole visual process which allows an object or diagram in the outside world to be comprehended by the brain as the 'eye-brain combination' or simply as the 'eye-brain'.
|
|
| The combination of eye and brain which is able to process the visual information about the outside world is indicated in blue. Compare with Leonardo da Vinci's diagram on Page 6. | The image of objects in the outside world is focused by the lens on the retina. There is a small 'blind spot' where the optic nerve leaves the eye. |
Is it Real?
With our eyes we are unable to observe directly the three-dimensional nature of the world about us. First, the lens of the eye must focus a flat picture on the retina. Then the brain must reconstruct an understanding of the three-dimensional reality. You must not think that we are talking here about stereoscopic vision, which is the effect of depth which we get by using two eyes. Even when we look with only one eye we still get a good impression of the three-dimensional world. The eye-brain combination is able to process a great deal of information and to present the result in a fraction of a second. As human beings, we are able to walk into a room and instantly recognize objects. We can say "that is a chair, and there is another one", instantly drawing on our knowledge of the shape and colours of chairs we have seen before and recognizing them in any position. This is a remarkable achievement and one which we are far from being able to imitate with any computer. There is a kind of 'robot vision', where a combination of T.V. camera and computer is able to distinguish between simple objects like cubes, pyramids and cylinders when seen from any direction. However, it is only at the most elementary stage of development and it will be many years before any such combination will be able to approach the power of the human eye and brain. It is clear that it does not matter whether we are looking either at the real three-dimensional world or at a twoódimension representation in the form of a drawing or a photograph. In either situation, the brain must process a flat image on the retina in order to be able to understand what the eye is seeing. What actually happens when we look at an impossible figure? What calculations does your brain have to make when you look at the figures below?

|
|
| Impossible tri-bar in a landscape | Japanese tri-bar |
We are sure that you felt them to exist at the same time as you knew that they did not! There is a fundamental contradiction which cannot be resolved. You know that the bars which make up the impossible tri-bar cannot meet in real space, but the eye-brain still tries to assign a meaning. Millions of years of evolution have prepared the human brain to understand the real world, but it is now faced with an image which it cannot interpret. It knows that the shape cannot exist and yet the image does not then dissolve into a meaningless set of lines with no three-dimensional power. It seems possible to accept and reject it, both at the same time. This gives the impossible figure a kind of real existence. It appears to have acquired a similar status to real objects like houses, trees and chairs, objects which the eye-brain has long been able to comprehend from the flat pictures on the retina. It is the curious real/unreal existence which is the intriguing characteristic of impossible figures.
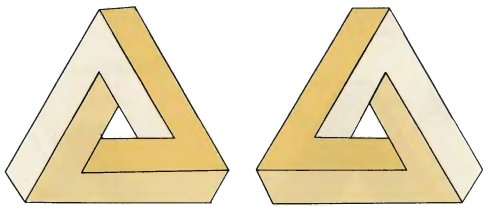
Tri-bars exist in pairs, each of which is a reflection of the other
An Impossible Model?
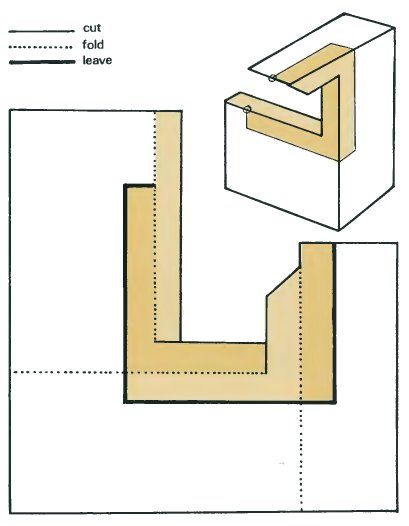
If you want to make a three-dimensional model of an impossible tri-bar, it is not necessary to use wood as I have done for the photograph on page 11. You can make a cardboard model. The net is given below and if you follow the instructions you will be able to make a three-dimensional object part of which will appear to be an impossible tri-bar when photographed or seen from a certain angle. Of course it is not really an impossible tri-bar. Impossible tri-bars really are impossible! The model needs to be strong, so you should make a photocopy of the page and then glue it to a piece of thin card before starting to make it up.
The Beginning
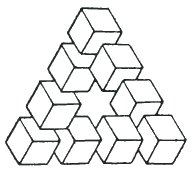
In the year 1934 the Swedish artist Oscar Reutersvärd drew this arrangement of nine cubes and the first impossible tri-bar had been created. He continued to experiment in this new field and made many hundreds of drawings. In 1958 L.S. & R.Penrose published a short article in the British Journal of Psychology: 'Impossible objects, a special kind of visual illusion'. In this article they described the impossible tri-bar and the idea of endless stairs. These ideas were taken up by other artists, especially Escher, and this fascinating subject became gradually known and appreciated by many more people.

In 1982 the Swedish Post Office commemorated the work of Reutersväd by issuing a series of three stamps showing his impossible figures. In the same year a book was published which showed a selection of his drawings and it was later translated into several languages.

The graphic artist M.C. Escher has brought the knowledge of impossible figures to a much wider audience. His lithograph 'Waterfall', which he produced in 1961 makes use of three linked tri-bars in the centre of the print. He has brought out the contradiction in the impossible tri-bar in a most marvellous way. The water appears to flow steadily downwards and yet ends up higher than where it started. Reaching the top, the water spills out of its channel to form a waterfall which drives a waterwheel. Escher's brilliant imagination has used one impossibility, the tri-bar, to create another, the perpetual motion machine.
This has become one of Escher's best known and best loved of prints and more than 160,000 reproductions have been sold.
With the help of two drawings we can show that the impossible tri-bar really does have a special kind of existence.
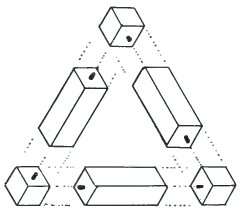
Here you can see how to construct a tri-bar. All you need are three small bars and three small cubes. The diagram looks most convincing. Most of us, even those who know it would not work, still feel that in some way it must be possible.

This diagram shows that it is even possible to calculate the volume and the surface area of an impossible tri-bar. Suppose that each cube is of side 1cm, then each side of the tri-bar is 5cm long. The volume is then 12cm3 and the surface area is 48cm2. Check it yourself. It is only a question of counting the number of cubes.
Tri-bar Fantasies
The impossible tri-bar can be used as a basis for all kinds of drawings. A few examples of the possible approaches are given on the next few pages.
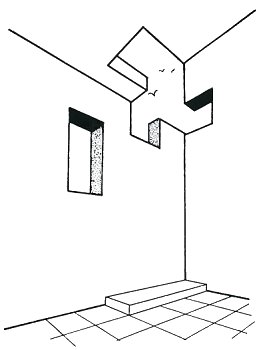
In 1984, I was asked to draw a jubilee poster for Oscar Reutersvärd to celebrate 50 years of impossible figures. This is the preliminary sketch. Note how the impossible tri-bar has disappeared to leave an impossible hole in the wall.
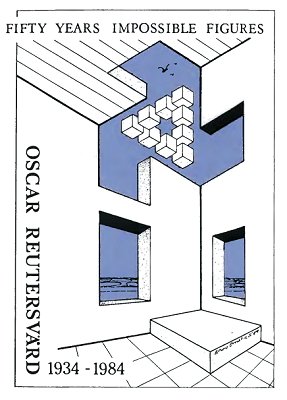
This was the jubilee poster. Reutersvärd's original figure, the one which started the impossible story, appears as an impossible heavenly body seen through an impossible opening in the wall!
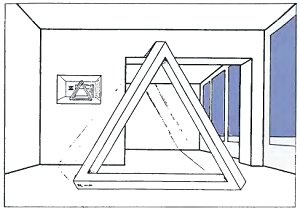
I tried to sketch an impossible tri-bar standing in the normal surroundings of the landing outside my flat, and then sent it to Oscar Reutersväd.
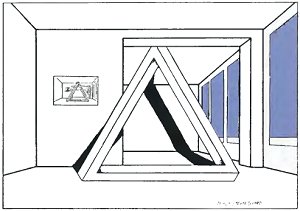
He sent it back a few days later, altered so that it was more interesting. The top of the tri-bar disappears behind the beam.
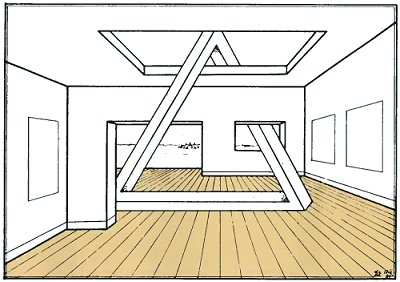
Inspired by this, I drew a third version in which a different kind of impossible figure (see chapter 7) is used to create a rather special kind of setting for the tri-bar. Now the room is a museum hall or possibly an art gallery, but one in which the placing of the model causes rather severe problems!

Perhaps in the year 2034, an impossible tri-bar will be erected on the moon to celebrate one hundred years of impossible figures. I borrowed the setting from Macaulay.
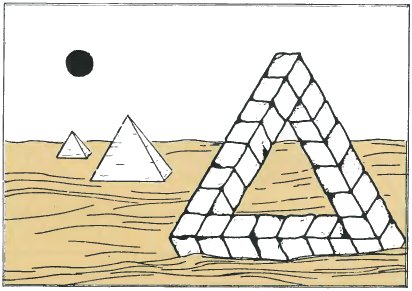
If ever the great pyramid of Cheops were to disappear then an impossible tri-bar of the same size could be placed on the site. It would use far less material.
