Гиперкуб
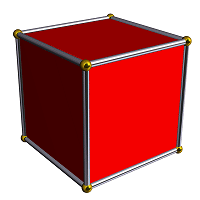 Проекция куба на плоскость |
В геометрии гиперкуб - это n-мерная аналогия квадрата (n = 2) и куба (n = 3). Это замкнутая выпуклая фигура, состоящая из групп параллельных линий, расположенных на противоположных краях фигуры, и соединенных друг с другом под прямым углом.
Эта фигура также известная под названием тессеракт (tesseract). Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.
Согласно Окфордскому словарю английского языка, слово "tesseract" было придумано в 1888 Чарльзом Говардом Хинтоном (Charles Howard Hinton) и использовано в его книге "Новая эра мысли" ("A New Era of Thought"). Слово было образовано от греческого "τεσσερες ακτινες" ("четыре луча"), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).
n-мерный гиперкуб также называется n-кубом.
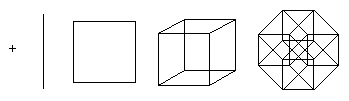
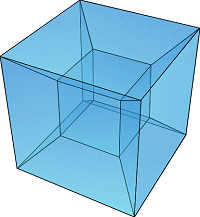 Проекция гиперкуба на плоскость |
Точка - это гиперкуб размерности 0. Если сдвинуть точку на единицу длины, получится отрезок единичной длины - гиперкуб размерности 1. Далее, если сдвинуть отрезок на единицу длины в направлении перпендикулярном направлению отрезка получится куб - гиперкуб размерности 2. Сдвигая квадрат на единицу длины в направлении перпендикулярном плоскости квадрата, получается куб - гиперкуб размерности 3. Этот процесс может быть обобщен на любое количество измерений. Например, если сдвинуть куб на единицу длины в четвертом измерении, получится тессеракт.
Семейство гиперкубов является одним из немногих правильных многогранников, которые могут быть представлены в любом измерении.
Элементы гиперкуба
Гиперкуб размерности n имеет 2n "сторон" (одномерная линия имеет 2 точки; двухмерный квадрат - 4 стороны; трехмерный куб - 6 граней; четырехмерный тессеракт - 8 ячеек). Количество вершин (точек) гиперкуба равно 2n (например, для куба - 23 вершин).
Количество m-мерных гиперкубов на границе n-куба равно
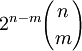
Например, на границе гиперкуба находятся 8 кубов, 24 квадрата, 32 ребра и 16 вершин.
| n-куб | Название | Вершина (0-грань) |
Ребро (1-грань) |
Грань (2-грань) |
Ячейка (3-грань) |
(4-грань) | (5-грань) | (6-грань) | (7-грань) | (8-грань) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-куб | Точка | 1 | ||||||||
| 1-куб | Отрезок | 2 | 1 | |||||||
| 2-куб | Квадрат | 4 | 4 | 1 | ||||||
| 3-куб | Куб | 8 | 12 | 6 | 1 | |||||
| 4-куб | Тессеракт | 16 | 32 | 24 | 8 | 1 | ||||
| 5-куб | Пентеракт | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-куб | Хексеракт | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-куб | Хептеракт | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-куб | Октеракт | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-куб | Эненеракт | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Проекция на плоскость
Формирование гиперкуба может быть представлено следующим способом:
- Две точки A и B могут быть соединены, образуя отрезок AB.
- Два параллельных отрезка AB и CD могут быть соединены, образуя квадрат ABCD.
- Два параллельных квадрата ABCD и EFGH могут быть соединены, образуя куб ABCDEFGH.
- Два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены, образуя гиперкуб ABCDEFGHIJKLMNOP.
Последнюю структуру нелегко представить, но возможно изобразить ее проекцию на двухмерное или трехмерное пространство. Более того, проекции на двухмерную плоскость могут быть более полезны возможностью перестановки позиций спроецированных вершин. В этом случае можно получить изображения, которые больше не отражают пространственные отношения элементов внутри тессеракта, но иллюстрируют структуру соединений вершин, как на примерах ниже.
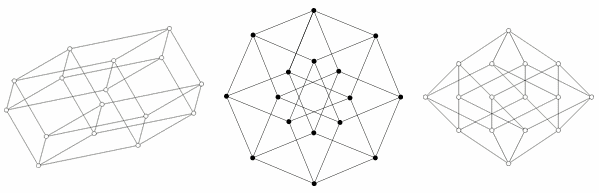
На первой иллюстрации показано, как в принципе образуется тессеракт путем соединения двух кубов. Эта схема похожа на схему создания куба из двух квадратов. На второй схеме показано, что все ребра тессеракта имеют одинаковую длину. Эта схема также заставляют искать соединенные друг с другом кубы. На третьей схеме вершины тессеракта расположены в соответствии с расстояниями вдоль граней относительно нижней точки. Эта схема интересна тем, что она используется как базовая схема для сетевой топологии соединения процессоров при организации параллельных вычислений: расстояние между любыми двумя узлами не превышает 4 длин ребер, и существует много различных путей для уравновешивания нагрузки.
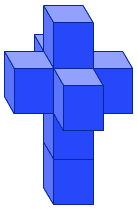 Развертка тессеракта |
Развертка гиперкуба
Тессеракт может быть развернут в восемь кубов, подобно тому как куб может быть развернут в шесть квадратов. Многогранник-равертка гиперкуба называется сетью. Существует 261 различных вариантов сетей. Справа показан один из вариантов
 Сальвадор Дали "Распятие" (1954) |
Гиперкуб в искусстве
Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт Хайнлайн в рассказе "Дом, который построил Тил" ("And He Built a Crooked House") описал дом, построенный по форме развертки тессеракта. В рассказе этот Далее этот дом сворачивается, превращаясь в четырехмерный тессеракт. После этого гиперкуб появляется во многих книгах и новеллах.
В фильме "Куб 2: Гиперкуб" рассказывается о восьми людях, запертых в сети гиперкубов.
На картине Сальвадора Дали "Распятие" ("Crucifixion (Corpus Hypercubus)", 1954) изображен Иисус распятый на развертке тессеракта. Эту картину можно увидеть в Музее Искусств (Metropolitan Museum of Art) в Нью-Йорке.
Заключение
Гиперкуб - одна из простейших четырехмерных объектов, на примере которого можно увидеть всю сложность и необычность четвертого измерения. И то, что выглядит невозможным в трех измерениях, возможно в четырех, например, невозможные фигур. Так, например, бруски невозможного треугольника в четырех измерениях будут соединены под прямыми углами. И эта фигура будет выглядеть так со всех точек обзора, и не будет искажаться в отличие от реализаций невозможного треугольника в трехмерном пространстве (см. "Невозможные фигуры в реальном мире").
Статья составлена по материалам Wikipedia
