Наведение порядка в невозможном
Zenon Kulpa
Институт Биокибернетики и Биомедицинских Технологий, Варшава, Польша
[Издано в журнале Perception, 1987, vol. 16, pp. 201-214]
Аннотация. Исследуется класс зрительных иллюзий, называемый 'невозможными фигурами', с целью упорядочения широко спектра подобных фигур, в частности упорядочение с целью облегчения описания, унификации терминологии и определения концептуального каркаса для дальнейших исследований, облегчая выбор и систематическое создание различных типов фигур (например, в систематических психологических экспериментах). Во-первых, определяется понятие 'невозможной фигуры', а также других связанных классов фигур (так называемых 'правдоподобных' и 'неправдоподобных' фигур). Во-вторых, определяются 'строительные элементы' невозможных фигур как базовые 'невозможные источники'. В заключение, кратко описываются два больших класса невозможных фигур – 'мультибары' (или 'невозможные многоугольники') и линейные фигуры.
1 Введение
С момента публикации короткой статьи отцом и сыном Пенроузами в 1958 году так называемые 'невозможные фигуры' все больше и больше привлекают внимание психологов, ученых-компьютерщиков и математиков. Психологи изучают их как новый тип зрительных иллюзий (Penrose and Penrose 1958; Gregory 1970; Young and Deręgowski 1981), изучая механизмы зрительного восприятия, в частности пространственной интерпретации изображений (например, Gregory 1970; Huffman 1971; Cowan and Pringle 1978; Young and Deręgowski 1981; Kulpa 1983; Térouanne 1983; Thro 1983). По схожим причинам они интересуют и ученых-компьютерщиков, которые работают в области компьютерного видения и пытаются создавать компьютерные модели с возможностями человеческого восприятия (Huffman 1971; Sugihara 1982a, 1982b; Kulpa 1983). Для математиков невозможные фигуры представляют для изучения новые типы абстрактных структур (Huffman 1971; Cowan 1977; Térouanne 1980, 1983). Также следует отметить их эффект увеличивает интерес к теории и практике изобразительных искусств и графического дизайна (Ernst 1976, 1985, 1986; Yturralde 1978; Reutersvärd and Kulpa 1984), а также обсуждаются в контексте логики и философии языка (Cresswell 1983).
Представление нескольких наиболее известных невозможных фигур (рис. 1) является достаточным для демонстрации разнообразия существующих типов фигур. Можно получить гораздо больше примеров невозможных фигур, поэтому важно найти принципы систематизации и классификации.
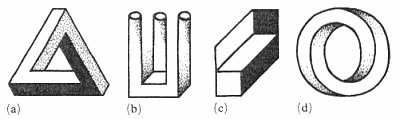
Рис. 1. Четыре примера невозможных фигур. (a)
Трибар Пенроуза, (b) вилка дьявола,
(c) фигура Тьери, (d) невозможное кольцо
В этой статье мы кратко обсудим некоторые базовые схемы систематизации. Изложение начинается (раздел 2) с определения невозможной фигуры (Kulpa 1983) и общей классификации, которая соотносит невозможные фигуры с возможными, а также со специальными классами фигур 'правдоподобными' и 'неправдоподобными' (Huffman 1971; Kulpa 1983). Также описывается проблема различных степеней невозможности. В разделе 3 определяются элементарные 'строительные блоки' невозможных фигур, называемые 'источниками невозможности' (Cowan and Pringle 1978; Kulpa 1983; Thro 1983). В заключение, в разделах 4 и 5, кратко описываются два широких класса невозможных фигур – мультибары (по-английски: multibars) (Cowan 1977; Draper 1978; Térouanne 1980; Kulpa 1981) и линейные фигуры (Robinson and Wilson 1973).
Схемы классификации, описанные в статье, основаны частично на моих исследованиях (Kulpa 1981, 1983), а также на работах других авторов, в частности Huffman (1971) и Cowan (1977). Представлены также и некоторые другие методы классификации. Guiraud и Lison (1976) пытались систематизировать с точки зрения графического дизайнера множество двусмысленных фигур, основанных на принципе фигур Тьери figure (Thiéry 1895; см. рис. 1с). С другой стороны, Sugihara (1982a, 1982b) предложил общую классификацию множества так называемых 'labelable figures' (которое включает много возможных и невозможных фигур) согласно чертам, характерным некоторым типам компьютерных алгоритмов автоматического анализа сцен.
2 Невозможные, правдоподобные и неправдоподобные фигуры
Прежде, чем пытаться классифицировать невозможные фигуры, важно сначала определить настолько точно, насколько это возможно.
2.1 Что такое невозможные фигуры?
Следующее определение охватывает интуитивное понятие невозможной фигуры:
Невозможная фигура – это плоский рисунок, который создает впечатление трехмерного объекта таким образом, что объект, предложенный нашим пространственным восприятием, не может существовать, так что попытка создать его ведет к (геометрическим) противоречиям, ясно видимыми наблюдателем.
Три фразы в этом определении, выделенные жирным шрифтом, являются ключевыми в верном понимании понятия невозможной фигуры. Их необходимо проанализировать более детально.
Во-первых, чтобы вынести на суд невозможности, изображение должно создавать впечатление пространственного объекта, которое должно включить в нас механизмы пространственного восприятия. В противном случае, называть его 'возможным' или 'невозможным' имеет смысла не более, чем задаваться вопросом – является ли рисунок квадрата возможным или невозможным. Более того, использование слова 'впечатление' указывает, что понятие невозможной фигуры имеет скорее психологическую природу, нежели математическую. Это заставляет нас сомневаться, что формальный (например, геометрический) анализ этого феномена дает возможность полного понимания (Kulpa 1983).
Во вторых, когда мы смотрим на изображение, которое создает впечатление пространственного объекта, наша система пространственного восприятия пытается найти пространственную форму, определить ориентацию и структуру, начиная с анализа отдельных фрагментов и намеков на глубину. Далее, эти отдельные части комбинируются и координируются в некотором порядке для создания общей гипотезы о пространственной структуре объекта (или объектов) целиком. Обычно, несмотря на то, что плоское изображение может иметь бесконечное множество пространственных интерпретаций (то есть, может быть представлено бесконечным количеством различных пространственных объектов), наш механизм интерпретации выбирает только одну – наиболее естественную для нас. Именно эта единственная интерпретация изображения далее проверяется на возможность или невозможность, а не сам рисунок. Невозможная интерпретация получается противоречивой по своей структуре – различные частичные интерпретации не подходят к общему непротиворечивому целому. В общем:
Свойство "быть невозможной фигурой" – это не свойство только изображения, а свойство пространственной интерпретации, выбранной человеком, смотрящим на изображение.
Мы называем те фигуры невозможными, чьи наиболее естественные интерпретации (для нас здесь и сейчас) оказываются невозможными. Однако, это не подразумевает, что не существует какой либо другой интерпретации этой же фигуры, которая может существовать. Таким образом, нахождение метода точного описания пространственных интерпретаций фигур является одним из основных путей для дальнейшей работы с невозможными фигурами и механизмами их интерпретации. Когда мы сможем описать (например, формально) различные интерпретации, мы сможем сравнивать их, соотносить фигуру и ее различные интерпретации (и, возможно, понять механизмы создания различных интерпретаций), проверять их соответствие или определять различные типы несоответствия и т.п. Значительный шаг в этом направление был сделан Térouanne (1983).
Фигура Тьери (Thiéry 1895; Gregory 1970; Guiraud and Lison 1976; Kulpa 1983; Reutersvärd and Kulpa 1984), показанная на рис. 1с, может служить примером различных интерпретаций одного и того же рисунка (см. рис. 2).
- 'Естественная' и невозможная: два параллелепипеда, которые обозреваются с разных точек и оказываются неправильно соединенными.
- Возможная, но двусмысленная: один параллелепипед с плоским дополнением в двух 'естественных' вариантах.
- 3. Возможная и предельно простая, хотя часто оказывающаяся незамеченной многими наблюдателями (Reutersvärd and Kulpa 1984): скошенный брусок (три его проекции представлены на рисунке, вторая проекция получена небольшим отклонением объекта от того положения, при котором получается исходная фигура).
Фактически, все невозможные фигуры имеют возможные интерпретации – "все невозможные фигуры – возможны" (Kulpa 1983). Таким образом, то факт, что фигура выглядит невозможной, обнаруживает некоторые ошибки в работе нашего механизма интерпретации пространства. Эти фигуры являются иллюзиями пространственной интерпретации, новым типом зрительных иллюзий (Penrose and Penrose 1958).
В третьих, когда мы называем фигуру невозможной, мы может указать неправильность в нашей интерпретации – противоречия должны стать сразу очевидными. Разыскивая фигуры, которые не подходят к этому условию, я обнаружил два других типа фигур, которые тесно связаны с невозможными фигурами, но которые, однако, не удовлетворяют этому определению. Я назвал их 'правдоподобными' и 'неправдоподобными' фигурами.
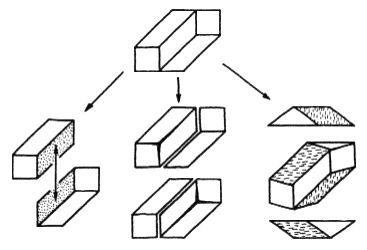
Рис. 2. Три интерпретации фигуры Тьери.
2.2 Правдоподобные и неправдоподобные фигуры
Два типичный примера правдоподобных фигур – усеченная пирамида и угол Хаффмана (Huffman 1971;Kulpa 1983) показаны на рисунке 3a и 3b.
В данном случае наш мозг совершает двойную ошибку: во-первых, он выбирает невозможные интерпретации этих фигур (треугольная пирамида с треугольным основанием и вырезанный внутренний угол ящика с толстыми стенками), во-вторых, он полагает эти невозможные интерпретации вполне реальными. Невозможность этих интерпретаций может быть легко показан (см. рис. 3c и 3d). В случае с пирамидой (рис. 3c) ребра A, B, и C, образованные пересечение трех различных плоскостей, должны пересекаться в одной точке, однако, этого не происходит (аналогичное рассуждение может быть применено и к невозможному треугольник на рис 1a). В случае с углом Хаффмана (рис. 3d) плоскости A и B пересекаются вдоль двух различных линий, в то время как две плоскости должны пересекаться только по одной линии.
Полностью противоположная ситуация с неправдоподобными фигурами. Наш мозг чаще всего выбирает для таких фигур возможные интерпретации, но трактует их с сомнением, находя их подозрительными или невозможными (Huffman 1971; Gillam 1979). Простые примеры представлены на рис. 4. Их обычные интерпретации соответственно – игральная кость с перекошенными гранями и брусок с наклонным вырезом (Huffman 1971) и перекошенный в пространстве пятиугольник, составленный из брусков (пентабар Цезаря, Térouanrte 1983) – вполне возможны, хотя и не выглядят таковыми для многих наблюдателей.
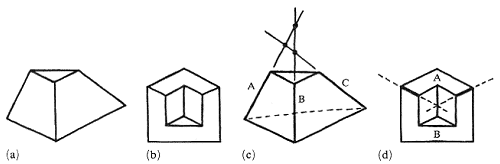
Рис. 3. Два примера правдоподобных фигур: (a)
усеченная пирамида, (b) угол Хаффмана
с объяснениями их невозможности [(c) и (d) соответственно]
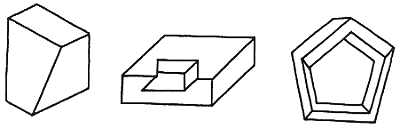
Рис. 4. Три примера неправдоподобных фигур
2.3 Общая классификация фигур
Наиболее общая классификация невозможный и связанных с ними фигур представлена в таблице 1 (Kulpa 1983). Однако из-за психологической природы этого феномена, эта классификация не является абсолютной. Разные люди в разных ситуациях могут классифицировать одни и те же рисунки по-разному. Также, внутри каждого класса различные фигуры могут разной степени соответствовать этому классе. Например, некоторые невозможные фигуры могут выглядеть менее невозможными, чем другие.
Таблица 1. Общая классификация фигур.
| Интерпретация, выносимая на суд невозможности |
Выбранная интерпретация | |
| Возможный | Невозможный | |
| Возможный | возможные фигуры | правдоподобные фигуры |
| Невозможный | неправдоподобные фигуры | невозможные фигуры |
2.4 Степени невозможности
Некоторые невозможные фигура кажутся 'очень невозможными' и сильно противоречивыми, и найти для них возможные интерпретации очень сложно (см рис. 1b, вилка дьявола). Другие фигуры выглядят менее невозможными, и хотя найти для них возможные интерпретации тоже непросто, они не выглядят совсем невообразимыми (см. рис. 1a, невозможный треугольник или трибар). Другие фигуры приводят в замещательство, но их возможные интерпретации гораздо проще найти, например, фигура Тьери (рис. 1c и 2). Также есть фигуры, которые выглядят 'почти невозможными', однако, найти для них возможные интерпретации настолько просто, что они уже после секундного размышления приходят на ум наблюдателю, который изначально был смущен их необычной структурой. Например, почти невозможный брусок (рис. 5a). Невозможная интерпретация, которая приходит на ум, близка к фигуре Тьери – два неправильно соединенных параллелепипеда, обозреваемые с разных точек зрения (рис. 5b), но вскоре появляется и возможная интерпретация (Kulpa 1983; Reutersvärd and Kulpa 1984), а именно, полукольцо квадратного сечения (рис. 5c) или скошенный брусок с квадратным сечением.
К сожалению, из-за психологической природы суждения о невозможности, цель формального определения количественной меры невозможного на сегодняшний момент кажется недостижимой несмотря на большое количество попыток в этом направлении (Huffman 1971; Cowan 1977; Cowan and Pringle 1978; Sugihara 1982a; Térouanne 1980, 1983).
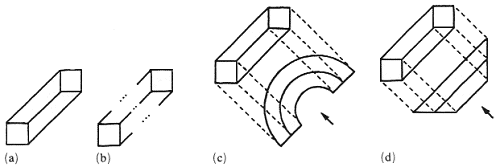
Рис. 5. Почти невозможный брусок. (b) невозможная интерпретация, которая первая
приходит на ум; (c), (d) две возможные интерпретации.
3 Источники невозможности
Рисунок кажется невозможным, когда локальные интерпретации взаимно несовместимы. Следовательно, важной черты пространственных интерпретаций, которые определены более или менее локально и могут противоречить аналогичным чертам других прилегающих фрагментов, приводят нас к определению возможных источников невозможности. Анализируя различные невозможные (и возможные) фигуры я смог разделить их три основных типа: противоречие объекта и фона, противоречие определения положения и противоречие формы поверхности (Kulpa 1983).
3.1 Противоречие объекта и фона
Среди источников невозможности этот является самым мощным, потому что он нарушает базовый принцип зрительного фона и элементов объекта. Для случайного наблюдателя это противоречие является наиболее заметной с первого взгляда, и является наиболее сложным для нахождения возможной интерпретации. На рис. 6a показан почти 'чистый' случай противоречия объекта и фона. На рис. 6b показан сравнительно недавно открытый вариант подобного противоречия (Kulpa 1983; Reutersvärd and Kulpa 1984; Ernst 1985, 1986), когда тень падает на объект и на фон.
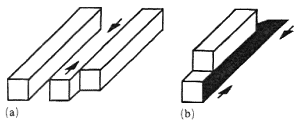
Рис. 6. Два примера фигур с противоречием объекта и фона. (a)
почти чистый пример,
(b) недавно открытый вариант
3.2 Противоречие определения положения
Противоречие определения положения наиболее общий источник невозможности, и может быть найден во многих невозможных фигурах в ризличных вариантах. Это противоречие возникает, когда относительное положение одного и того же элемента объекта определяется по-разному в разных областях. Например, в невозможной лестнице (Penrose and Penrose 195S; Kulpa 1983) и блоке Хаффмана (Huffman 1971; Kulpa 1983) противоречие связано с вертикальной позицией фрагментов объектов.
Ступенька A лестницы (рис 7a), очевидно, находится ниже ступеньки B. Также очевидно, что она находится выше ступеньки Следуя по ступенькам в правый угол лестницы, видно, что ступенька C находится выше ступеньки B, а следовательно, так как ступенька A выше ступеньки C, то она должна быть и выше ступеньки B. В случае с блоком Хаффмана, ребро A, очевидно, находится ниже ребра B, которое отделено вертикальным ребром. Но оба ребра A и B принадлежат одной и той же верхней поверхности блока, и, следовательно, должны находиться на одном уровне.
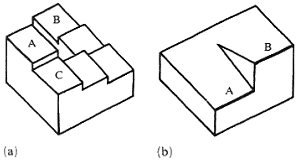
Рис. 7. Два примера противоречия определения вертикальной позиции:
(a) невозможная лестница; (b) блок Хаффмана.
3.2.1 Противоречие определения глубины
Очень части мы сталкиваемся с вариантом противоречия определения положения, при котором определяется глубина, то есть определяется расстояние в направлении перпендикулярном плоскости рисунка, которое различается для одного и того же фрагмента рисунка. Например, в невозможном треугольнике (рис. 8) углы L и R предполагают, что левый брусок удаляется от нас, в правый наоборот приближается к нам. Таким образом конец L' должен находиться дальше R'. Но в замкнутом треугольнике концы L' и R' соединены и находятся на одном уровне глубины.
В общем, противоречие определения положения менее заметно, чем противоречие объекта и фона. Это противоречие иногда можно встретить в правдоподобных фигурах. Также для этого противоречия проще найти возможную интерпретацию, несмотря на подчас более сложную структуру (Gregory 1970; Kulpa 1983; Ernst 1985, 1986).
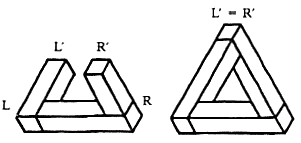
Рис. 8. Противоречие определения глубины в невозможном треугольнике.
3.3 Противоречие формы поверхности
Этот феномен часто появляется в результате возникновения других источников невозможности. Это случается, когда предполагаемое пространственное соответствие области рисунка (представляющего фрагмент поверхности объекта) различается в разных областях рисунках. Обычно это противоречие может быть легко преодолено, если представить плавный переход поверхности (без границ и складок) из одной предполагаемой формы в другую.
Существует для вида этого источника невозможности – противоречие искривленной плоскости и противоречие плоскости и изогнутой поверхности.
3.3.1 Противоречие искривленной плоскости
В данном случае плоская поверхность объекта допускает два противоречивых предположения своей пространственной ориентации (например, горизонтальное и вертикальное). В наиболее чистом виде это противоречие демонстрирует дибар Эрнста (Ernst 1985; рис. 9a).
3.3.2 Противоречие между плоскостью и искривленной поверхностью
Здесь противоречие между два базовыми формами поверхности объекта – плоская и изогнутая. Этот вид может быть проиллюстрировать простой фигурой, где одна балка квадратного сечения плавно переход в две балки круглого сечения.
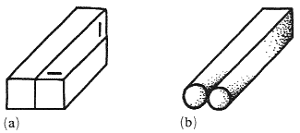
Рис. 9. Два примера противоречия формы поверхности: (a) искривленная плоскость
в дибаре Эрнста; (b) противоречие между плоскостью и искривленной поверхностью.
3.4 Смешанные типы
Во многих невозможных фигурах обычно можно увидеть несколько разных источников невозможности, иногда один источник становится продолжением другого. Хорошим примером может служить вилка дьявола (рис. 1b), где в трех местах присутствует противоречие объекта и фона, когда плоские поверхности становятся цилиндрическими, кроме того, одна из полос, параллельных плоскости рисунка, изгибается, и зубцы вилки допуская различные предположения о глубине. Не удивительно, что вилка дьявола 'настолько сильно невозможна'.
Блок Хаффмана (рис. 7b) при некотором усилии может быть интерпретирован также в терминах противоречия плоскости и изогнутой поверхности. Его верхняя поверхность, ограниченная парой прямых параллельных ребер, кажется горизонтальной плоскостью. Но расположение ребер A и B показывает, что поверхность не может быть плоской, отсюда и противоречие.
Отметим, что 'чистый' пример противоречия объекта и формы (рис. 6a) не совсем чистый: фрагмент, помеченный стрелками кроме того, что переходит из объекта в фон, также еще и меняет свое вертикальное расположение. Рис. 6b демонстрирует другой пример взаимозависимости различных типов невозможности: противоречие объекта и фона, получающееся из перехода собственной тени в отброшенную тень, также служит причиной противоречия вертикальной и горизонтальной позиции затемненной области.
4 Мультибары
Мультибар – это класс фигур, предложенный Cowan (1977) (под названием 'тор с углами'), также изучался и другими учеными (Draper 1978; Térouanne 1980, 1983; Kulpa 1981). Часто его называют 'невозможный многоугольник'. Эти фигуры состоят из определенного количества квадратных брусков, соединенных друг с другом концами в многоугольник (рис. 10).
Соединения брусков многоугольников могут быть видны с четырех различных направлений. В результате каждый угол появляется на рисунке в одной из четырех конфигураций, обозначаемых символическими кодами N, M, Z, и S соответственно (рис. 11), при помощи которых мы можем определить символический код мультабара.
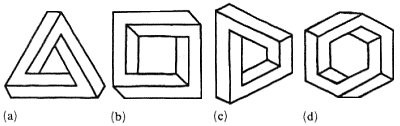
Рис. 10. Четыре примера мультибаров
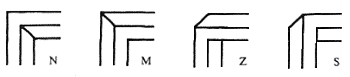
Рис. 11. Четыре базовых конфигураций углов мультибара
4.1 Символическое кодирование мультибаров
Последовательность кодов всех углов мультибара (по умолчанию в направлении часовой стрелки) является исходной точкой кодирования. Примеры на рис. 10 описываются следующими последовательностями SSS, NSNS, NZZM и NMSNMS соответственно.
Так как поворот фигуры на плоскости рисунка не меняет его структуры, то последовательности кодирования циклически инвариантна, то есть циклический сдвиг последовательности, фактически, представляет ту же самую фигуру (выбор первого угла для последовательности не важен). Например, все последовательности NZZM, ZZMN, ZMNZ и MNZZ представляют одну и ту же фигура (рис. 10c). Однако, если мы введем порядок следования кодов [обычно используется последовательность N < M < Z < S [Cowan 1977; Kulpa 1981)], и из всех сдвигов последовательности выберем наименьшую (лексикографически), то мы получим 'каноническое' описание фигура, которое устанавливает четкое соответствие между фигурами и их последовательностями кодов.
Для последующего упорядочения мультибаров мы может использовать различные типы геометрически [или топологических (Cowan 1977)] отношений. Базовые отношения задаются геометрическими преобразованиями.
4.2 Геометрические трансформации мультибаров
Существуют следующие операции трансформации мультибаров – инверсия (по-английски: inversion) (зеркальное отражение) и обверсия (по-английски: obversion) (или 'вид сзади'), обозначаемые символами I и O соответственно. Также существует операция иверсии (eversion), получаемая наложением двух предыдущих операций, которая обозначается символом E и описывается выражением E = IO = OI. Хотя эти операции и геометрические, они могут легко выражаться в терминах преобразования символических кодов. То есть, операция I меняет углы Z на S и наоборот, операция O меняет углы M на N и наоборот, а вместе эти операции переворачивают последовательность кодов углов (рис. 12). Эти операции вместе с соответствующими им геометрическими преобразованиями образуют коммутативную (перестановочную) группу преобразований.
Внутри каждой группы фигур, что касается операций I, O, и E, фигура с первым лексикографическим кодом, выбирается в качестве канонической формы (обозначаемой символически T), а все группы далее перечисляются в (лексикографической) последовательности их канонических форм. Таким образом, получена коммутативная схема классификации, отражающая базовую математическую структуру наборов n-баров.
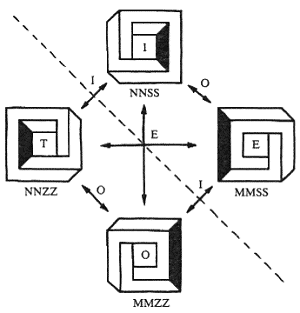
Рис. 12. Геометрические трансформации четырехугольника.
4.3 Создание мультибаров при помощи компьютера
Комбинаторный алгоритм, создающий все канонические последовательности кодов углов в лексикографическом порядке, является, фактически, генератором мультибаров (возможных и невозможных), и может быть легко запрограммирован на компьютере. Этот алгоритм, совмещенный со схемой классификации, основанной на геометрических трансформациях (TIOE), быть реализован автором статьи (Kulpa 1981). Программа производила различные таблицы мультибаров, включая перечень всех треугольников (трибаров), приведенных в таблице 2.
Таблица 2. Список трибаров, сгенерированный программой (общее количество трибаров – 24)
| Номер | T | I | O | E |
| 1 | NNN | =T | MMM | =O |
| 2 | NNM | =T | NMM | =O |
| 3 | NNZ | NNS | MMZ | MMS |
| 4 | NMZ | NSM | =T | =I |
| 5 | NMS | NZM | =T | =I |
| 6 | NZZ | NSS | MZZ | MSS |
| 7 | NZS | =T | MSZ | =O |
| 8 | NSZ | =T | MZS | =O |
| 9 | ZZZ | SSS | =T | =I |
| 10 | ZZS | ZSS | =T | =I |
Рассмотрим невозможный треугольник (SSS) с кодом 9I и его зеркальное отражение – треугольник ZZZ с кодом 9T (см. рис. 13a). Обверсия (вид сзади) треугольника ZZZ является тем же самым треугольника ZZZ, в то время как иверсия – идентична зеркальному отражению, то есть SSS. Четырехугольники NSNS и NZZM (рис. 10b и 10с) присутствуют в таблице четырехугольников в ячейках 15I и 14I соответственно, а шестиугольник NMSNMS (рис. 10d) – в ячейке 139T.
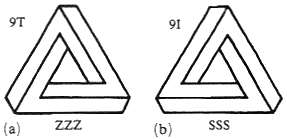
Рис. 13. Два треугольника из строки 9 со своими кодами.
4.4 Вогнутые и скругленные мультибары
В моих рассуждениях о мультибарах я придерживался негласного допущения, что все мультибары образуют выпуклые многоугольника. Исключив это допущение, мы получим массу вогнутых мультибаров (см. рис. 14).
Вогнутые мультибары легко включить в нашу схему кодирования. Можно добавить специальную отметку к кодам вогнутых углов, например, апостроф. Фигуры на рис. 14 получат следующие коды NZSS'Z, MNZZ'SN и NZN'ZM'ZM соответственно.
Добавив новые формы углов, мы может создать, например, скругленные мультибары, которые состоят из скругленных углов двух возможных форм, обозначаемых символами Z0 и S0 (рис. 15). Таким образом, семейство мультибаров снова увеличивает, чтобы включить в себя такие фигуры как рис. 16, которые могут быть закодированы символически Z0Z0, NS0S, и ZZMS'0MS соответственно.
Семейство мультибаров может быть расширено дальше, если включить в него многоугольники с самопересечениями. Некоторые примеры могут быть найдены в следующих источниках Draper (1978), Térouanne (1980) и т.д. В этом случае проблема каталогизации возможных типов пересечений и кодирования фигур становится более сложной и рассматриваться здесь не будет.
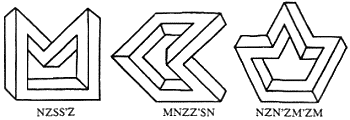
Рис. 14. Три примера вогнутых мультибаров с их кодами.
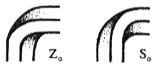
Рис. 15. Два типа скругленных углов
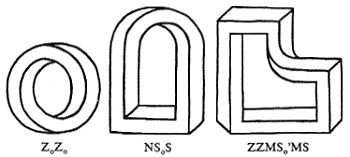
Рис. 16. Три примера мультибаров со скругленными углами с их кодами.
4.5 Подсчет мультибаров
Комбинаторная природа метода перечисления мультибаров позволяет сравнительно легко вывести формулы для перечисления количество различных мультибаров (Kulpa 1981). Обозначим как Mc(n) количество мультибаров с n углами c типов, где n = 1,2,...; c = 4 для выпуклых мультибаров, c = 8 для мультибаров с вогнутыми углами, c = 12 – для мультибаров со скругленными углами выпуклыми и вогнутыми углами.
Существует всего c ↑ n различных последовательностей из n элементов c типов. Количество соответствуют мультибаров – меньше из-за того, что все циклические сдвиги последовательности, хотя обычно и отличаются, представляют один и тот же мультибар. Более того, если бы для каждой последовательности все n циклических сдвигов были бы различны, то есть для каждый мультибар имел бы ровно n различных циклически эквивалентных последовательной, мы бы имели:
![]()
Однако, для некоторых групп циклически эквивалентных последовательностей меньше, чем n элементов (например, последовательность NNN является циклическим эквивалентом самой себя, в последовательность из четырех элементов ZSZS циклически эквивалентна только с одной последовательностью SZSZ). Суммируя эквивалентные последовательности, получим нижнюю и верхнюю оценку для Mc(n):
|
|
(1) |
где оператор 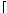 x
x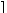 обозначает наименьшее целое число не меньше, чем x.
обозначает наименьшее целое число не меньше, чем x.
Когда n простое число, все циклически эквивалентные последовательности длиной меньше n гомогенны, то есть формы pp p, где p один из типов элементов c. Для всех c гомогенных последовательностей их группы циклической эквивалентности содержат только одну последовательность, то есть значение n - 1 меньше количества двех остальных негомогенных последовательностей. Таким образом значение n × Mc(n) больше c ↑ n ровно на c(n - 1), и в этом случае Mc(n) может быть точно вычислено (при условии, что n простое число):
|
|
(2) |
К сожалению, если n не простое число, то ситуация становится более сложной, и точную формулу получить гораздо сложнее. К счастью, нижняя оценка Mc(n) оказывается достаточно точной. Когда n – простое число, она отличается от Mc(n) меньше, чем на значение c [см. выражение (2)]; для остальных значений n эта разница больше, но все равно остается небольшой (и зависит от количества делителей n). В таблице 3 показаны точные значения мультибаров для c = 4, а также нижнюю оценку количества для c = 4,8,12.
Таблица 3. Количество мультибаров Mc(n) с n углами c типов; c = 4 для обычных выпуклых мультибаров, c = 8 для мультибаров с вогнутыми углами и c = 12 для мультибаров (выпуклых и вогнутых) со скругленными углами.
| n | Точное значение c = 4 |
Нижняя оценка 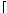 (c ↑ n) / n (c ↑ n) / n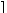 |
||
| c = 4 | c = 8 | c = 12 | ||
| 1 | 4 | 4 | 8 | 12 |
| 2 | 10 | 8 | 32 | 72 |
| 3 | 24 | 22 | 171 | 576 |
| 4 | 70 | 64 | 1024 | 5184 |
| 5 | 208 | 205 | 6554 | 49767 |
| 6 | 700 | 683 | 43691 | 248832 |
| 7 | 2344 | 2341 | 299594 | 5118830 |
5. Линейные фигуры
Разные виды невозможных фигур (Robinson and Wilson 1973; см. рис. 17a) могут быть интерпретированы как последовательность полос, то есть как последовательность продолговатых областей, разделенных прямыми параллельными линиями согласно общей схеме на рис. 17b, где символы I1, I2, ..., In и J1, J2, .... Jn обозначают соответствующую (пространственную) интерпретация полос, как это предполагается в контекстах рисунка, в которых находятся их окончания. Когда интерпретации I и J отличаются возникает противоречие, которое, возможно, в конечном итоге и производит невозможную фигуру.
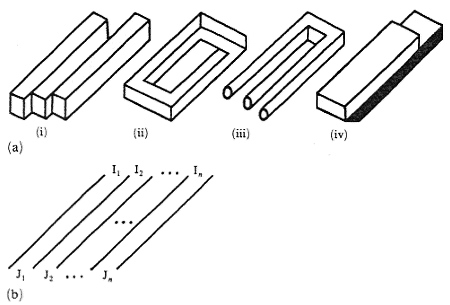
Рис. 17. (a) четыре примера линейный фигур; (b)
общая схема линейной фигуры.
5.1 Символическое кодирование линейных фигур
Мы можем найти много различных интерпретация (или классов интерпретаций) полос, которые могут присутствовать на рисунке. Если мы обозначим их соответствующими символами, например:
O объект,
B фон,
P плоский,
C искривленный,
Vr вертикальная плоскость, видимая справа,
Vl вертикальная плоскость видимая слева,
Ha горизонтальная плоскость видимая сверху,
Hb горизонтальная плоскость видимая снизу,
S тень,
и т.д., тогда мы можем создать целостную систему символического кодирования широкого класса фигура, а также метод для их классификации и, в конечном итоге, алгоритм систематического создания.
Коды в общей форме
![]()
для четырех примеров фигур на рис. 17 могут быть следующими
| (i) | 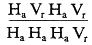 |
||
| (ii) | 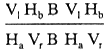 |
||
| (iii) | 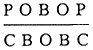 |
or | 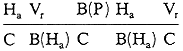 |
| (iv) | 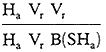 |
Многие невозможные фигуры (или их значимые части), которые демонстрируют противоречие объекта и фона, могут быть интерпретированы как линейные фигуры. Однако, фигуры, в которых присутствует противоречие определения позиции (например, невозможный треугольник или невозможная лестница) обычно не могут быть интерпретированы данным способом.
6 Заключение
Мы кратко рассмотрели несколько схем упорядочения невозможных фигур для их классификации и структурного описания. Для всего множества плоских фигур, которые предполагают их пространственную интерпретацию, рассмотренные схемы включают:
- Общее разделение на классы возможных, невозможных, правдоподобных и неправдоподобных фигур;
- Установление базовых источников невозможности;
- Структурное описание двух основных классов невозможных фигур – мультибаров и линейных фигур.
Такое упорядочение облегчит описание фигур, унифицирует терминологию и создаст концептуальный каркас для дальнейших исследований в данной области. Также оно должно облегчить поиск и систематическое создание различных типов фигур (например, в систематических психологических опытах).
Данная статья является лишь введением в данную область и большие исследования в этой области еще впереди. Существуют также другие схемы классификации, на описанные в данной статье (Guiraud and Lison 1976, Sugihara 1982a, 1982b), но много невозможных фигур еще остаются неисследованными и неклассифицированными (Ernst 1976, 1985, 1986; Draper 1978; Yturralde 1978; Reutersvärd and Kulpa 1984).
Подготовка этой статьи частично поддерживалась исследовательским проектом No 06.9 Польской Академии Наук.
Библиография
- Cowan T M, 1977 "Organizing the properties of impossible figures" Perception 6 41-56
- Cowan T M, Pringle R, 1978 "An investigation of the cues responsible for figure impossibility" Journal of Experimental Psychology. Human Perception and Performance 4 112-120
- Cresswell M J, 1983 "A Highly impossible scene" in Meaning, Use and Interpretation of Language eds R. Bäuerle, C. Schwarze, A. von Stechow (Berlin: De Gruyter) pp. 62-77
- Draper S W, 1978 "The Penrose Triangle and a Family of Related Figures" Perception 7 283-296
- Ernst B, 1976 The Magic Mirror of M.C. Escher (New York: Ballantine Books)
- Ernst B, 1985 Avonturen met Onmogelijke Figuren (Amsterdam: Aramith Uitgevers)
- Ernst B, 1986 Het Begoochelde Oog Onmogelijke en Meerzinnige Figuren (Amsterdam: Meulenhoff/Landshoff)
- Gillam B, 1979 "Even a possible figure can look impossible!" Perception 8 229-232
- Gregory R L, 1970 The Intelligent Eye (London: Weidenfeld and Nicolson)
- Guiraud J, Lipson P, 1976 Systematique des Figures Reversibles (Bruxelles: Gestetner)
- Huffman D A, 1971 "Impossible objects as nonsense sentences" in Machine Intelligence 6 eds B Heltzer, D Michie (Edinburgh: Edinburgh Unversity Press) pp. 295-323
- Kulpa Z, 1981 "Generacja i klasyfikacja figur niemożliwych z klasy tzw. 'rogatych torusów'" ("Generation and classification of impossible figures of the so-called 'cornered toruses' class") internal report (in Polish) Institute of Biocybernetics and Biomedical Engineering, Warsaw, 28 pages plus computer listings
- Kulpa Z, 1983 "Are impossible figures possible?" Signal Processing 5 201-220
- Penrose L S, Penrose R, 1958 "Impossible objects a special type of visual illusion" British Journal of Psychology 49 31-33
- Reutersvärd O, Kulpa Z, 1984 Challenge to Geometry – Impossible Figures exhibition catalogue (Łódź, Poland Art Museum of Łódź)
- Robinson J O, Wilson J A, 1973 "The impossible colonnade and other variations of a well known-figure" British Journal of Psychology 64 363-365
- Sugihara K, 1982a "Classification of impossible objects" Perception 11 65-74
- Sugihara K, 1982b "Mathematical structures of line drawings of polyhedrons - toward man-machine communication by means of line drawings" IEEE Transactions of Pattern Analysis and Machine Intelligence 4 458-469
- Térouanne E, 1980 "On a class of 'impossible' figures: a new language for a new analysis" Journal of Mathematical Psychology 22 24-46
- Térouanne E, 1980 "'Impossible' figures and interpretations of polyhedral figures" Journal of Mathematical Psychology 24 370-405
- Thiéry A, 1895 "Über geometrisch-optische Täuschungen" Philosophische Studien 11 307-370
- Thro E B, 1983 "Distingushing two classes of impossible objects" Perception 12 733-751
- Young A W, Deręgowski J B, 1981 "Learning to see impossible" Perception 10 91-105
- Yturralde J M, 1978 "Ambigous structures" in Hypergraphics - Visualizing Complex Relationships in Art, Science and Technology ed D W Brisson (Boulder: CO Westview Press) pp. 177-185
