Fractals

Cameron Browne

Some parts of basic impossible figure can be cut and replaced by another parts of the same figure. This procedure can be applied to new parts of the figure many times for constructing impossible fractal figure of desired iteration.

Below, there's figures for impossible fractals created by Cameron Browne found at
http://members.optusnet.com.au/digex/impossible-fractals-figures/

Figure 1. The tri-bar, the Koch snowflake and the Sierpinski gasket.

Figure 2. Two iterations of an impossible snowflake (with acute and obtuse generators shown).

Figure 3. An alternative snowflake design that emphasizes the perceptual effect (with generator shown).

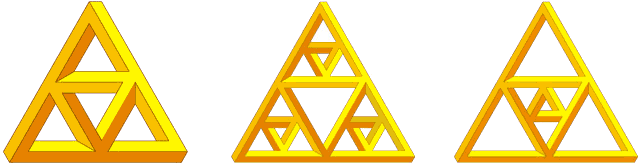
Figure 4. Impossible gaskets are more troublesome.

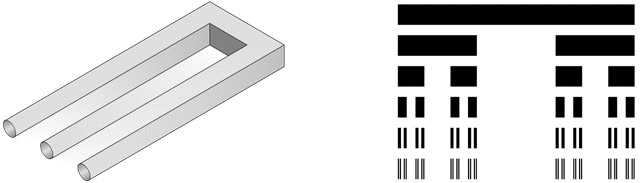
Figure 5. The Devil's fork and the Cantor set.

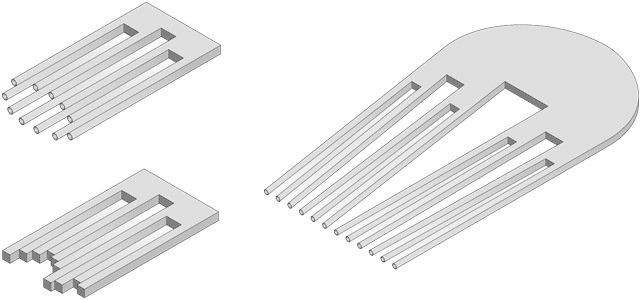
Figure 6. The Devil's gatling gun (two levels), timber offcuts (two levels) and comb (three levels).

Figure 7. Four-bar designs (with sharp and truncated generators) applied to the square Sierpinski curve.

Figure 8. An impossible multibar cube and the Menger sponge after one and three iterations.

Figure 9. Subcube designs and Buch's "Cube in blue".

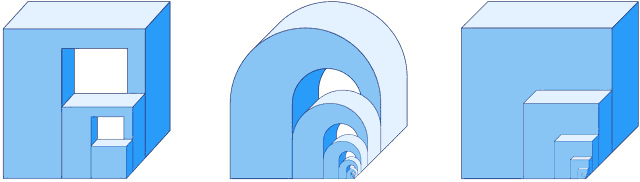
Figure 10. Ernst's "Nest of impossible cubes" and two variations.

Figure 11. An impossible multibar Peano-Gosper curve.

Figure 12. Reutersvärd's "Meander" and a Hilbert meander.

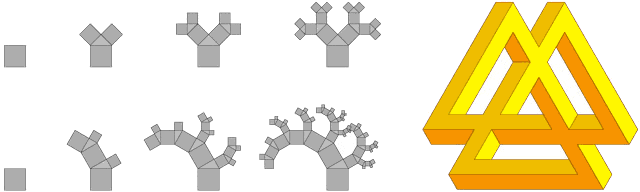
Figure 13. 45° Pythagorean tree, balanced 30° Pythagorean tree and extended tri-bar.

Figure 14. An impossible mushroom (45° Pythagorean tree).

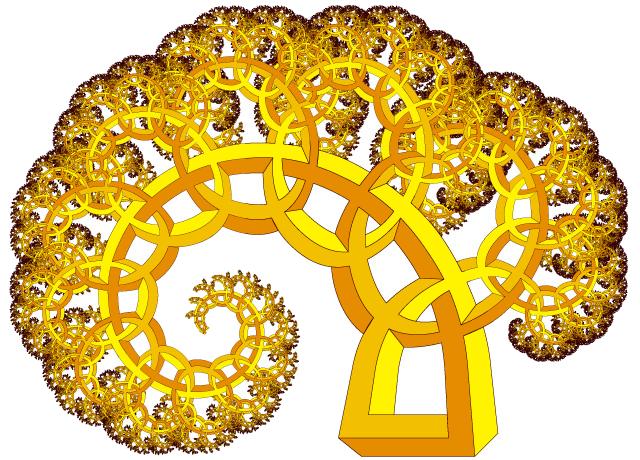
Figure 15. An impossible fern (balanced 30° Pythagorean tree).

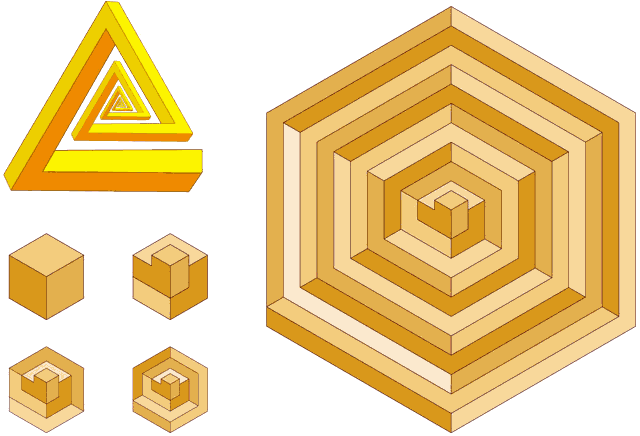
Figure 16. A spiral tri-bar and hexagonally bound isometric spirals.