Adventures with Impossible Figures

If we draw a figure which cannot actually exist in space, is it always obvious that we have done so? Is there a simple test which we could apply which would tell us with certainty whether or not a particular figure is impossible?

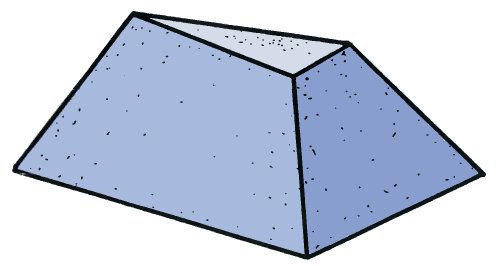
Most people would be able to accept this as a sketch of a real truncated pyramid. Yet I can tell you that it is really an impossible figure and prove it to your satisfaction. Can you see how? The solution is given on page 94, but do try to find it yourself first.

In order to decide about certain figures it seems that we cannot rely on the automatic response of the eye. We need to think, to reason and to try to find a method or test which would help us to make the correct decision.

The drawing above is not an impossible figure, but it does demonstrate how the automatic response of the eye is dulled once the drawing becomes too complicated. The figure consists of a single long and narrow loop which has been folded up in a manner reminiscent of the intestines. The problem is to decide whether A is inside or outside the loop.

To solve it we have to do more than just look. We have to reason. One way to decide would be to treat it like a maze problem and to try to find a route to the outside. If we can find no route to the outside, then we could say that A must be inside. However, most of us have had difficulty with maze problems in the past and the doubt would always remain that there might be a yet undiscovered route which would work.

For this problem there is a better solution. Let us draw any line, straight or curved, from A to the outside. For example, see AB above. Now let us count the number of lines we cross. Every time we cross a line, we are either crossing from the inside to the outside or from the outside to the inside. An even number of crossings on the route to the outside must mean that A is outside the loop. An odd number means that A is inside. Using this simple test, it is very easy to make the correct decision.

This problem was chosen as an example because it does have solutions on different levels and with different degrees of certainty. Perhaps we could use the insights so gained to devise a test which we could apply to impossible figures?

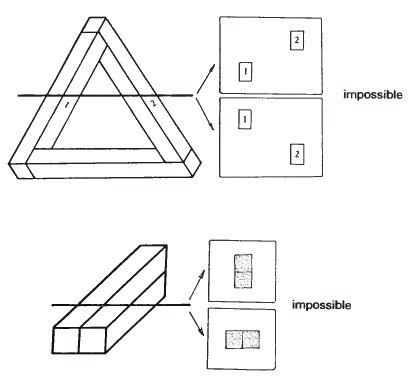
Many people have tried to devise a simple test like the one on the previous page, but so far without total success. Some tests appear to apply only to specific figures like the tri-bar, four-bar or multi-bar.

Perhaps you might like to experiment with the following test.

Draw or imagine a plane cutting through the figure. The line on each drawing represents the plane, although the plane does not necessarily have to be at right-angles to the paper. Cover the part of the figure to one side of the line with a piece of paper. Then sketch the cross-section which the plane makes with that part of the figure which remains. Then cover the other half and sketch that cross-section.

If both sketches are identical, then the figure is possible. If they are different in any respect, then it is impossible.

To illustrate how it works, here are five examples. Four of them are impossible and one is possible.

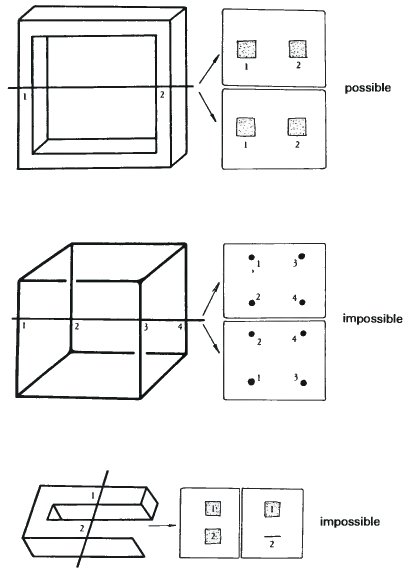
This method still demands a good understanding of each figure which is being tested and does require an element of subjective judgement. It does not work very well on figures like the one on page 90 where the impossibility is not very great. However, I hope that it will point the way one day towards a really satisfactory solution to this tricky problem.

Something Unique

The study of impossible figures has added something new and unique to the visual world of man. It offers an enrichment of the human spirit and a valuable field for the human imagination to explore. It is certainly not a branch of mathematics, although mathematical methods can be used to describe and analyse the figures. Nor is it necessarily art. Impossible figures can be drawn in a harmonious and expressive way, but they can just as well be rather ugly. They do awaken a response in most people, a certain sense of wonder - and they certainly help us in our attempt to understand how the eye-brain combination processes visual information. In so doing it may well help with the development of programs which would enable computer controlled robots to 'see'. Perhaps it is not surprising that of more than one hundred articles written about impossible figures since 1970, most of them have been published in computer magazines.

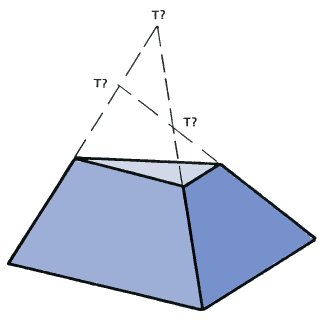
Solution to the problem on page 90.

Continuing the three lines of the sides of the pyramid leads to three different places, each of which must be the vertex. Hence it must be an impossible figure.