Adventures with Impossible Figures

An impossible figure exists because the visual signposts and clues which tell us about its position in space give contradictory information. So far we have met and used various indicators, mostly without really being aware that we have done so. But there are three main signposts which we use, quite unconsciously in most instances.

1. The covering and joining of planes.
2. The continuity of planes.
3. The orientation of planes.

Later we shall deal with the continuity of planes in more depth, but for the moment the context will offer sufficient explanation. Let us examine how these three types of misleading signposts can operate, individually and in combination.

1. Covering and Joining.

These three illustrations of crossed bars draw attention to what we unconsciously interpret about the positions of the bars.

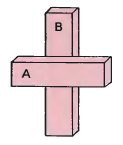(a) A is in front of B because B is covered by A

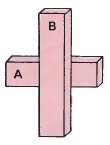(b) A is behind B because B covers A.

(c) A and B are the same distance away because we can see that A and B join.

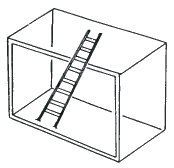
(d) Here we can appreciate the power of misleading signposts to lead our minds astray. The ladder begins inside and ends outside. it is an impossibility. But it is an impossibility simply because of one indicator. The ladder appears to pass in front of the top line. Without that, there would be no unresolved conflict and no impossibility.

2. The Continuity of Planes

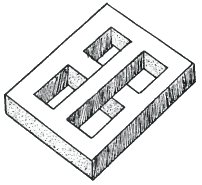
This impossible figure springs to life because we have used two different indicators of position at the same time. Around the perimeter the continuity of planes tells us that the top is flat. But in the centre one beam passes in front of the other. There is conflict and so an impossible figure is born.

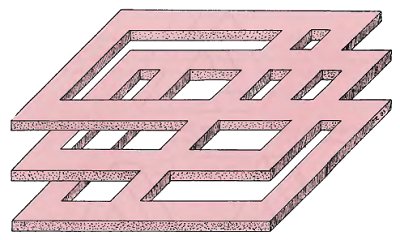
The confusion can be made stronger still by adding further three-dimensional signposts of relative position. If we look at the left side of this figure there are three layers, apparently one above the other in a vertical line. This is further reinforced by the crossing of one layer above another as far as the centre. But on the right side the visual signposts all point to a single plane. The mind is delightfully confused.

Of course there are many different versions of this type of figure and it is interesting to combine these ideas with those of the impossible four-bars from chapter 2.

3. The Orientation of Planes

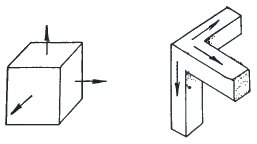
The eye seizes on any opportunity to comprehend the orientation of planes. On the left we can see how a cube immediately defines three perpendicular directions in space, directions which the eye expects to be maintained consistently across the whole illustration. On the right, three bars meeting at a corner define the directions even more strongly.

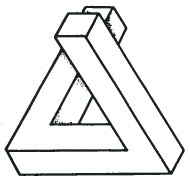
This figure causes no problems. The planes firmly define three directions in space and one bar passes in front of the other just as we expect.

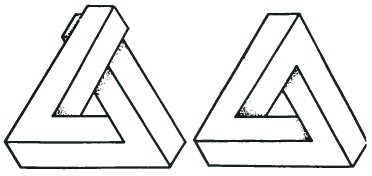
Here there are problems. The directions are clearly defined, but in both cases the orientations are not maintained across the whole figure. The signposts of covering and joining give different information from the signposts of orientation. The result is that we have two different impossible figures. At this point we can admire once again the elegance and simplicity of the impossible tri-bar.