Mathematical art of M.C. Escher
Introduction
 Self Portrait |
Maurits Cornelis Escher, who was born in Leeuwarden, Holland in 1898, created unique and fascinating works of art that explore and exhibit a wide range of mathematical ideas.
While he was still in school his family planned for him to follow his father's career of architecture, but poor grades and an aptitude for drawing and design eventually led him to a career in the graphic arts. His work went almost unnoticed until the 1950's, but by 1956 he had given his first important exhibition, was written up in Time magazine, and acquired a world-wide reputation. Among his greatest admirers were mathematicians, who recognized in his work an extraordinary visualization of mathematical principles. This was the more remarkable in that Escher had no formal mathematics training beyond secondary school.
As his work developed, he drew great inspiration from the mathematical ideas he read about, often working directly from structures in plane and projective geometry, and eventually capturing the essence of non-Euclidean geometries, as we will see below. He was also fascinated with paradox and "impossible" figures, and used an idea of Roger Penrose's to develop many intriguing works of art. Thus, for the student of mathematics, Escher's work encompasses two broad areas: the geometry of space, and what we may call the logic of space.
Tesselations
 Alhambra scetch |
Regular divisions of the plane, called "tessellations", are arrangements of closed shapes that completely cover the plane without overlapping and without leaving gaps. Typically, the shapes making up a tessellation are polygons or similar regular shapes, such as the square tiles often used on floors. Escher, however, was fascinated by every kind of tessellation - regular and irregular - and took special delight in what he called "metamorphoses," in which the shapes changed and interacted with each other, and sometimes even broke free of the plane itself.
His interest began in 1936, when he traveled to Spain and viewed the tile patterns used in the Alhambra. He spent many days sketching these tilings, and later claimed that this "was the richest source of inspiration that I have ever tapped." In 1957 he wrote an essay on tessellations, in which he remarked:
In mathematical quarters, the regular division of the plane has been considered theoretically
. . . Does this mean that it is an exclusively mathematical question? In my opinion, it does not. [Mathematicians] have opened the gate leading to an extensive domain, but they have not entered this domain themselves. By their very nature thay are more interested in the way in which the gate is opened than in the garden lying behind it.
Whether or not this is fair to the mathematicians, it is true that they had shown that of all the regular polygons, only the triangle, square, and hexagon can be used for a tessellation. (Many more irregular polygons tile the plane - in particular there are many tessellations using irregular pentagons.) Escher exploited these basic patterns in his tessellations, applying what geometers would call reflections, glide reflections, translations, and rotations to obtain a greater variety of patterns. He also elaborated these patterns by "distorting" the basic shapes to render them into animals, birds, and other figures. These distortions had to obey the three, four, or six-fold symmetry of the underlying pattern in order to preserve the tessellation. The effect can be both startling and beautiful.
 |
 |
 |
|
 |
|||
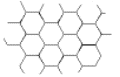
 Regular division of the plane with the birds |
 Reptiles |
 Cycles |
 Development 1 |
In Reptiles the tessellating creatures playfully escape from the prison of two dimensions and go snorting about the destop, only to collapse back into the pattern again. Escher used this reptile pattern in many hexagonal tessellations. In Development 1, it is possible to trace the developing distortions of the square tessellation that lead to the final pattern at the center.
Polyhedra
 Four Regular Solids |
The regular solids, known as polyhedra, held a special fascination for Escher. He made them the subject of many of his works and included them as secondary elements in a great many more. There are only five polyhedra with exactly similar polygonal faces, and they are called the Platonic solids: the tetrahedron, with four triangular faces; the cube, with six square faces; the octahedron, with eight triangular faces; the dodecahedron, with twelve pentagonal faces; and the icosahedron, with twenty triangular faces. In the woodcut Four Regular Solids, Escher has intersected all but one of the Platonic solids in such a way that their symmetries are aligned, and he has made them translucent so that each is discernable through the others. Which one is missing?
 Order and chaos |
There are many interesting solids that may be obtained from the Platonic solids by intersecting them or stellating them. To stellate a solid means to replace each of its faces with a pyramid, that is, with a pointed solid having triangular faces; this transforms the polyhedron into a pointed, three-dimensional star. A beautiful example of a stellated dodecahedron may be found in Escher's Order and Chaos. Here the stellated figure rests within a crystalline sphere, and the austere beauty of the construction contrasts with the disordered flotsam of other items resting on the table. Notice that the source of light for the composition may be guessed, for the bright window above and to the left of the viewer is reflected in the sphere.
 Stars |
Intersecting solids are also represented in many of Escher's works, one of the most interesting being the wood engraving Stars.
Here are solids constructed of intersecting octahedra, tetrahedra, and cubes, among many others. One might pause to consider, that if Escher had simply drawn a bunch of mathematical shapes and left it at that, we probably would never have heard of him or of his work. Instead, by such devices as placing the chameleons inside the polyhedron to mock and alarm us, Escher jars us out of our comfortable perceptual habits and challenges us to look with fresh eyes upon the things he has wrought. Surely this is another source of the mathematicians' admiration for Escher's work - for just such a perceptual freshness lies at the back of all great mathematical discovery.
The shape of space
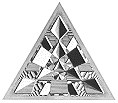 Three intersecting planes |
Among the most important of Escher's works from a mathematical point of view are those dealing with the nature of space itself. His woodcut Three Intersecting Planes is a good place to begin a review of these works, for it exemplifies the artist's concern with the dimensionality of space, and with the mind's ability to discern three-dimensionality in a two-dimensional representation. As we will see in the next section, Escher often exploited this latter feature to achieve astonishing visual effects.
 Circle limit III |
Inspired by a drawing in a book by the mathematician H.S.M Coxeter, Escher created many beautiful representations of hyperbolic space, as in the woodcut Circle Limit III. This is one of the two kinds of non-Euclidean space, and the model represented in Escher's work is actually due to the French mathematician Poincaré. To get a sense of what this space is like, imagine that you are actually in the picture itself. As you walk from the center of the picture towards its edge, you will shrink just as the fishes in the picture do, so that to actually reach the edge you have to walk a distance that, to you, seems infinite. Indeed, to you, being inside this hyperbolic space, it would not be immediately obvious that anything was unusual about it - after all, you have to walk an infinite distance to get to the edge of ordinary Euclidean space too. However, if you were a careful observer you might begin to notice some odd things, such as that all similar triangles were the same size, and that no straight-sided figure you could draw would have four right angles - that is, this space doesn't have any squares or rectangles. A strange place indeed!
 Snakes |
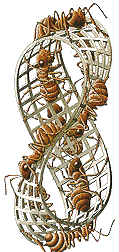 Möbius Strip II |
Even more unusual is the space suggested by the woodcut Snakes. Here the space heads off to infinity both towards the rim and towards the center of the circle, as suggested by the shrinking, interlocking rings. If you occupied this sort of a space, what would it be like?
In addition to Euclidean and non-Euclidean geometries, Escher was very interested in visual aspects of Topology, a branch of mathematics just coming into fullflower during his lifetime. Topology concerns itself with those properties of a space which are unchanged by distortions which may stretch or bend it - but which do not tear or puncture it - and topologists were busy showing the world many strange objects. The Möbius strip is perhaps the prime example, and Escher made many representations of it. It has the curious property that it has only one side, and one edge. Thus, if you trace the path of the ants in Möbius Strip II, you will discover that they are not walking on opposite sides of the strip at all - they are all walking on the same side. It is easy to make a Möbius strip; just cut a strip of paper with scissors, give it a half-twist, and then glue or tape the ends. What do you predict will happen if you attempt to cut such a strip in two, lengthwise?
 Print gallery |
Another very remarkable lithograph, called Print Gallery, explores
both the logic and the topology of space. Here a young man in an art gallery is
looking at a print of a seaside town with a shop along the docks, and in the
shop is an art gallery, with a young man looking at a print of a seaside
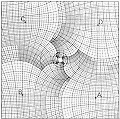  |
All of Escher's works reward a prolonged stare, but this one does especially. Somehow, Escher has turned space back into itself, so that the young man is both inside the picture and outside of it simultaneously. The secret of its making can be rendered somewhat less obscure by examining the grid-paper sketch the artist made in preparation for this lithograph. Note how the scale of the grid grows continuously in a clockwise direction. And note especially what this trick entails: A hole in the middle. A mathematician would call this a singularity, a place where the fabric of the space no longer holds together. There is just no way to knit this bizarre space into a seamless whole, and Escher, rather than try to obscure it in some way, has put his trademark initials smack in the center of it.
The logic of space
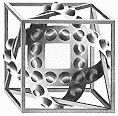 Cube with Ribbons |
By the "logic" of space we mean those spatial relations among physical objects which are necessary, and which when violated result in visual paradoxes, sometimes called optical illusions. All artists are concerned with the logic of space, and many have explored its rules quite deliberately. Picasso, for instance.
 High and Low |
Escher understood that the geometry of space determines its logic, and likewise the logic of space often determines its geometry. One of the features of the logic of space which he often applied is the play of light and shadow on concave and convex objects. In the lithograph Cube with Ribbons, the bumps on the bands are our visual clue to how they are intertwined with the cube. However, if we are to believe our eyes, then we cannot believe the ribbons!
Another of Escher's chief concerns was with perspective. In any perspective drawing, vanishing points are chosen which represent for the eye the point(s) at inifinity. It was the study of perspective and "points at infinity" by Alberti, Desargues, and others during the renaissance that led directly to the modern field of projective geometry.
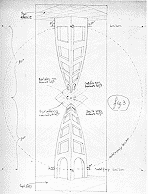 |
By introducing unusual vanishing points and forcing elements of a composition to obey them, Escher was able to render scenes in which the "up/down" and "left/right" orientations of its elements shift, depending on how the viewer's eye takes it in. In his perspective study for High and Low, the artist has placed five vanishing points: top left and right, bottom left and right, and center. The result is that in the bottom half of the composition the viewer is looking up, but in the top half he or she is looking down. To emphasize what he has accomplished, Escher has made the top and bottom halves depictions of the same composition.
 |
 Waterfall |
A third type of "impossible drawing" relies on the brain's insistence upon using visual clues to construct a three-dimensional object from a two-dimensional representation, and Escher created many works which address this type of anomaly.
One of the most intriguing is based on an idea of the mathematician Roger Penrose's - the impossible triangle. In this lithograph, Waterfall, two Penrose triangles have been combined into one impossible figure. One sees immediately one of the reasons the logic of space must preclude such a construction: the waterfall is a closed system, yet it turns the mill wheel continuously, like a perpetual motion machine, violating the law of conservation of energy. (Notice the intersecting cubes and octahedrons on the towers.)
Self-reference and information
 Drawing Hands |
Our final consideration of Escher's art involves its relationship to the fields of information science and artificial intelligence. This aspect of his work has been largely overlooked in previous studies, but the case for its importance to these fields was forcefully made by Douglas R. Hofstadter in his 1980 Pulitzer Prize winning book, Gödel, Escher, Bach: An Eternal Golden Braid.
 Fish and Scales |
A central concept which Escher captured is that of self-reference, which many believe lies near the heart of the enigma of consciousness - and the brain's ability to process information in a way that no computer has yet mimicked successfully.
The lithograph Drawing Hands and the woodcut Fish and Scales each captures this idea in a different way. In the former the self-reference is direct and conceptual; the hands draw themselves much the way that consciousness considers and constructs itself, mysteriously, with both self and self-reference inseparable and coequal. In Fish and Scales, on the other hand, the self-reference is more functional; one might rather call it self-resemblence. In this way the woodcut describes not only fish but all organisms, for although we are not built, at least physically, from small copies of ourselves, in an information-theoretic sense we are indeed built in just such a way, for every cell of our bodies carries the complete information describing the entire creature, in the form of DNA.
 Three Spheres II |
On a deeper level, self-reference is found in the way our worlds of perception
reflect and intersect one another. We are each like a character in a book who is
reading his or her own story, or like a picture of a mirror reflecting its own
landscape. Many of Escher's works exhibit this theme of intersecting worlds, but
we will here consider only one of the exemplars. As is common in Escher's
treatment of this idea, the lithograph Three Spheres II makes use of the
reflective properties of a spherical mirror. Here, as Hofstatder noted, "every
part of the world seems to contain, and be contained in, every other
And so we end where we began, with a self portrait: the work a reflection of the artist, the artist reflected in his work.
Conclusion
We have here considered only a handful among the hundreds of drawings, lithographs, woodcuts, and mezzotints Escher left to us upon his death in 1972. Much more could be said, and has been said, about the depth, meaning, and importance of his work. The reader is encouraged to explore further the rich legacy of M.C. Escher, and to ponder anew the intersections he has drawn for us among the world of imagination, the world of mathematics, and the world of our waking life.
Reprinted from http://www.mathacademy.com/pr/minitext/escher/
