M.C.Escher's Legacy. A Centennial Celebration
Computer Games Based on Escher's Spatial Illusions
I have always loved the way Escher invites me to participate in his worlds. In Ascending and Descending, Escher invites me to join a procession of monks as they walk around an endless staircase. In Convex and Concave he asks me to compare objects on the left with their inverted counterparts on the right. His tessellations challenge me to trace the dual logic of the curves that outline the tiles.
Escher once said that if he had a second lifetime he might have become an animator. Perhaps in a third lifetime he might have designed games.
Many artists have found that games let viewers experience their work in a deeper way. The Italian sculptor Miguel Berrocal makes intricate metal sculptures that come apart into many pieces. The Japanese artist Toshio Iwai made a computer game called SimTunes that invites players to experiment with patterns of color and sound. When I play with a Berrocal sculpture or an Iwai game, I gain an active understanding of how pieces relate to one another that is very different than if I merely viewed them passively. "I hear and I forget, I see and I remember, I do and I understand."
Escher Interactive
I got my chance to design an Escher game in 1994, when author Joost Elfers invited me to contribute to a CD-ROM called Escher Interactive. Over the next year I worked with programmer David Oster in California, and Mike Chanowski and Henk Alles at Eyeware Interactive in the Netherlands where the disk was being produced, to create a collection of sixteen "Impossible Puzzles". They are called impossible not because they are impossible to solve, but because they are based on impossible figures and other spatial illusions from Escher's work.

Escher Interactive is the first major software project based on Escher's work. Published in 1996, the disk includes an art gallery, timeline, interviews with experts, animations of Escher works, three games, and a drawing program for creating tessellations (see Fig. 1).
Impossible Puzzles
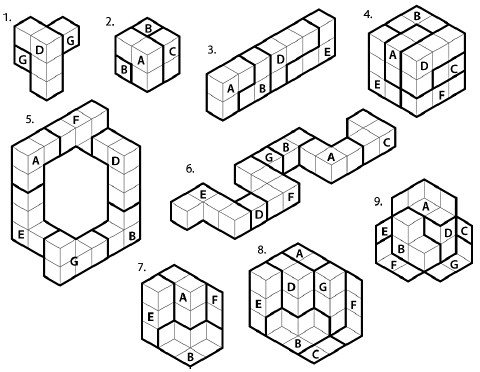
The player's goal in each Impossible Puzzle is to assemble a collection of pieces into a given shape. Often the final shape is a visual illusion. Each piece is made of cubes seen in flat isometric projection. Pieces may be overlapped, but not rotated.

The first eight puzzles are the eight letters of the name M.C. ESCHER. The last eight are based on specific Escher prints. Each puzzle has a unique solution, in order to make the puzzles harder, as well as to make the answers easier for the computer to verify. The sixteen puzzles are illustrated in Fig. 2.
The idea for the Impossible Puzzles first appeared in my earlier game Heaven & Earth [10]. I designed over six hundred puzzles on the theme of Illusions for Heaven & Earth, working with lead game designer Michael Feinberg, producer Brad Fregger, programmers Ian Gilman and Michael Sandige, artist Mark Ferrari and musician Richard Marriott.
M.C.
The first two puzzles, M, C, are shown in Fig. 3. The goal is to overlap the small pieces to make a copy of the big shape. Pieces cannot be rotated; they must stay in their original orientation. Of course you could play this game with cutout paper pieces, but on the computer, pieces are easier to manipulate. Pieces automatically snap into place, and pop to the front layer when you click on them. The computer also automatically enforces the rule that pieces cannot be rotated.
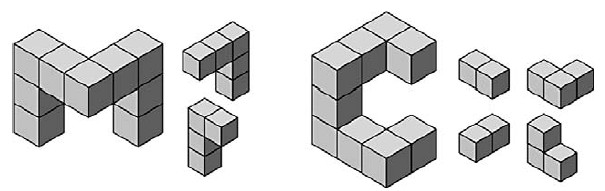
As in most computer games, the first few puzzles are easy and then the puzzles gradually get harder. The main purpose of the first two puzzles is to teach the rules of the game. Fig. 4 shows their solutions; notice how pieces overlap.
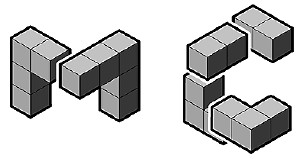
ES
The puzzles E, S are shown in Fig. 5. Although pieces appear to be solid, the player must think of them as flat shapes cut out of paper - pieces sometimes overlap in ways that make no sense in three-dimensional space. For instance, the solution sequence for E is shown in Fig. 6.
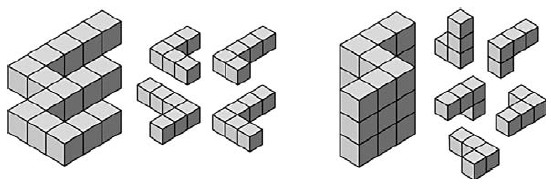
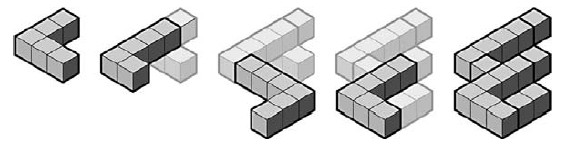
CH
The puzzles C, H are shown in Fig. 7. Notice that the way you perceive the shapes in three dimensions shifts while you are putting the pieces together. For instance, in the solution sequence for C, cubes that appear to be in the same plane at one stage shift into different planes at a later stage because other pieces have been added.
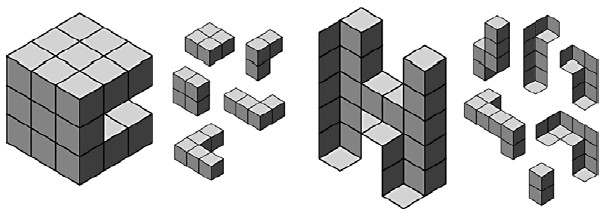
I have seen other illusions in which your perception of a situation changes when you add or remove a piece, but I do not know whether anyone has given this type of illusion a name. I like to call them "interactive illusions". Because interactive illusions are under your control, the effect is particularly startling. (I have included interactive illusions in several of my computer games. For example, Heaven & Earth includes interactive illusions based on figure/ground
H introduces concave/convex ambiguity, which appears in Escher's print Convex and Concave. Assembling this puzzle is a disorienting experience: pieces often overlap along faces with contradictory interpretations. It was particularly difficult for me to find a way to break this shape into pieces so the solution was unique.
ER
The last two puzzles, which complete Escher's name, are in Fig. 8. The second E is an "improbable figure" - it appears to be an E only when seen from certain angles. Notice that the shape is composed entirely of L tetrominoes in various orientations. To keep the solution unique, no two pieces are identical.
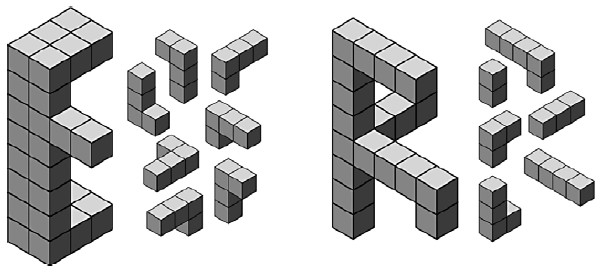
R is an impossible figure, similar to the impossible triangle that appears in Escher's print Waterfall. To make it more challenging for the player I made the initial arrangement of pieces appear to be close to the solution. In fact most pieces are not where they should be in the solution.
Escher himself occasionally played visual tricks with letterforms. Fig. 9 shows a print he made to announce a four-person art exhibition. Notice how the same letters can be perceived differently depending on their orientation: the E also serves as an M, the H as an I, the U as a C, and so on. A similar crossword design appears at the beginning and end of his epic scroll Metamorphose.

A similar design on the name "M.C. Escher" appears in my book of illusionary lettering designs Inversions. An animation of this design appears in Escher Interactive; you can also find it on the CD-ROM accompanying this book.
Triangles
The Impossible Triangle, also called the Penrose tribar, was invented by British psychologist L. S. Penrose and physicist son Roger Penrose in 1958. (Dutch artist Oscar Reutersvärd discovered the shape much earlier, but did not publish his work until later.) Their original article [9], which they sent to Escher, included drawings of both the impossible triangle and an endlessly rising staircase.
The puzzles "Impossible Triangle" and "Relativity" are shown in Fig. 10. Try playing the demo version of the impossible triangle puzzle on the CD-ROM that accompanies this book. As you join one bar to the next you will find that the loop always closes with one bar in front of another where it should really be behind. Use the two extra parallelograms to patch up this defect.

Escher's print Relativity also involves a triangle, but not an impossible one. Instead, it plays on the ambiguity of which way is up. The corresponding puzzle simplifies the triangle of stairs in Escher's print, and adds a new twist: pieces that reverse the sense of convex and concave, similar to Escher's Convex and Concave.
Flat and Solid
In his prints Dragon (Fig. 11) and Two Doric Columns, Escher questions whether the image you are seeing is flat or solid. To turn these works into puzzles I had to figure out a way to simplify the images into parallelograms. For each, I made different compromises (see Fig. 12).

The puzzle "Dragon" retains the pattern of folded slits in a flat surface, but discards the dragon itself. The puzzle "Columns" uses a different illusion from the one in the original work. Instead of exploiting flat versus solid, the puzzle exploits concave versus convex. Nonetheless it retains the form of two colums, each resting on the opposite side of the other's tail. This illusion is strikingly captured in drawings by Sandro Del Prete and paintings by Jos de Mey.
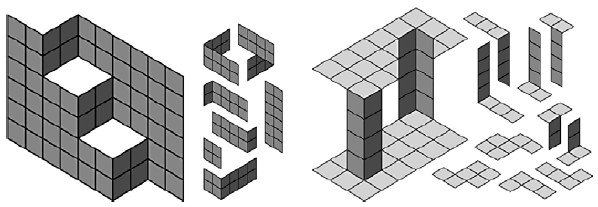
Notice that Escher's depiction of the columns, as well as mine, is completely symmetrical. One of the pairs of pieces in the "Columns" puzzle, however, is not symmetrical.
Staircases
Escher's Convex and Concave contains the classic ambiguous staircase illusion, broken into a symmetrical arrangement of pieces. The corresponding puzzle also has pairs of matching pieces (Fig. 13). Escher's Ascending and Descending contains the impossible endlessly rising staircase. The corresponding puzzle reduces the staircase to just one step on each leg. If we reduce the staircase even further, we get the impossible staircase with the fewest number of steps that can be composed of cubes (Fig. 14).

Of course the endlessly rising staircase is impossible only if we assume that what seem to be straight lines, right angles, and connected cubes actually are as they appear. If we allow the cubes to be slightly distorted into wavy surfaces, then we can make a three-dimensional model that looks just like this figure when viewed from a particular angle.

Note that in both the original Escher work and my puzzle the left two legs of the stairs' circuit are shorter than the right two legs. The asymmetry is aesthetically unappealing, but unavoidable. In my study of four-dimensional impossible figures - three-dimensional "drawings" that appear impossible to a four-dimensional person - I found that the four-dimensional analog of the impossible staircase has no such asymmetry.
Impossible Figures
The final two puzzles involve impossible figures. The mill race in Escher's Waterfall is constructed from three impossible triangles. The corresponding puzzle abstracts this impossible geometry (Fig. 15). Notice that the ends of the puzzle pieces are all shaved slightly differently.
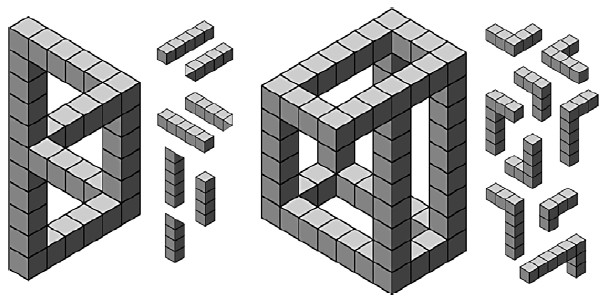
The man seated in Escher's vignette Man with Cuboid (Fig. 16) is similar to the one sitting at the base of the stairs in the print Belvedere. He holds a small model similar to the one in my puzzle "Belvedere" (Fig. 15). Since the exact model that he is holding had already appeared in Heaven & Earth, I twisted it differently for this Escher Interactive puzzle.

Notice that in the "cube" there are two points where one bar crosses in front of another. Because the seams of the cubes are visible, the back bar can be seen as merging into the front bar at these points. I exploit this ambiguity in the solution (Fig. 17).

Try It Yourself
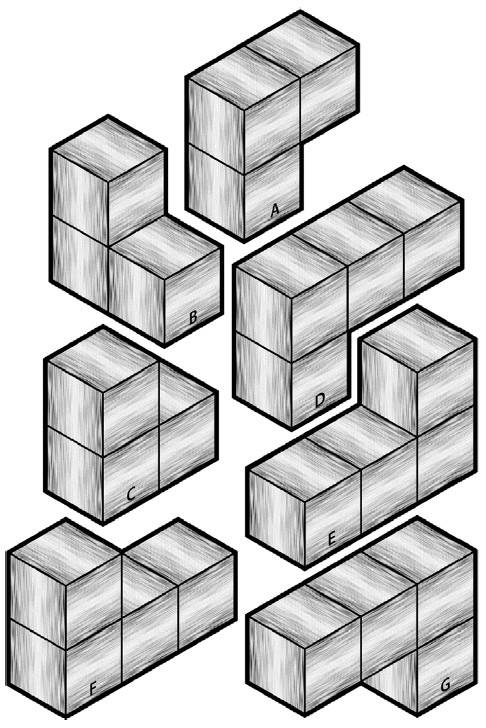
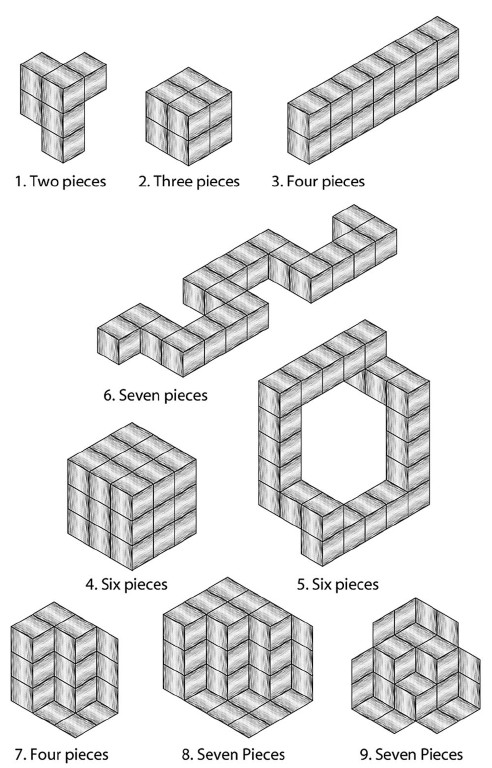
Here is a version of the Impossible Puzzles you can play without a computer. It originally appeared in Games Magazine. Photocopy Fig. 18 onto heavy paper and cut out the pieces. Assemble the pieces to make the various configurations in Fig. 19. You can rotate or overlap pieces, but you can't fold or cut them. Each puzzle tells you how many pieces you may use. Answers appear below.
References
- Ernst, Bruno, Adventures with Impossible Figures. Berlin: Taschen 1985.
- Eyeware Interactive BV, Escher Interactive: Exploring the Art of the Infinite (CDROM for Windows). New York: Harry N. Abrams, London: Thames & Hudson, Paris: Hachette Multimedia, Cologne: Dumont Verlag, Utrecht: A. W. Bruna, 1996.
- Gardner, Martin, "From Burrs to Berrocal", Scientific American, January 1978. Reprinted in Penrose Tiles to Trapdoor Ciphers, W. H. Freeman and Company, 1989.
- Iwai, Toshio, SimTunes (CD-ROM for Windows). Electronic Arts / Maxis, 1996.
- Kim, Scott, "An Impossible Four-Dimensional Illusion". In Brisson, David. Hypergraphics: Visualizing Complex Relationships in Art, Science and Technology. Westview Press, 1978.
- Kim, Scott, "Convex Concave", Games Magazine, October 1993, p. 20.
- Kim, Scott, Inversions: A Catalog of Calligraphic Cartwheels. Key Curriculum Press, 1996.
- Kim, Scott, www.scottkim.com
- Penrose, L. S., and Penrose, R., "Impossible Objects: A special type of illusion", British Journal of Psychology [49] (1958), 31.
- Publishing International, Heaven & Earth (floppy disks for Mac or Windows). Buena Vista Software, 1992. (out of print)