Animated graphic illustration of Quantum ChromoDynamics (QCD)
György Darvas and Tamás F. Farkas
Graphic illustration of the symmetries of sub-elementary particles.
Quarks are invisible. So are their properties, too. To visualise the quantum properties for physicists, and for the public, we can turn to graphical representations. Since (according to our latest knowledge) their symmetries, flavours and colours belong to the most important properties of the quarks, they should be placed in the centre of their graphic representation. This can be done in a purely schematic way (like in usual textbooks), and also with the application of art.
We try to fulfil the latter program. For the general public and students: the artistic visualisation brings these "mysterious" physical objects closer to their understanding. For physicists: the artistic representation of the quarks and their symmetries, flavours and colours gains its importance by its predicative force. Predictive force means, that the artistic representation makes physicists possible to reveal new secrets of the internal structure of the quarks and their properties. Mathematical and physical connections among them can be made visible. Please, note that the properties of the quarks called colours, etc. are only metaphoric names, and not identical with colours perceived with our eyes, flavours perceived with our tongues, etc. These metaphors are applied in the process of visualisation.
One of us developed a series of sets of graphic units that are appropriate kits to model the different properties of physical particles. One of those sets is demonstrated in these pages. This active illustration series is a result of a years-long co-operation between a physicist and a graphic artist.
Quarks
Although quarks never appear in the nature unbound (i.e., in single) we have to start explaining their representation in solo. According to the Standard Model of physics the structure of matter is built of quarks.
Scent of the quarks

Let's choose the above graphical unit to represent a single quark in our present visualisation. The unit (a shape formed by a line, composed of quadratic prisms, returning into itself) has a three-fold rotational symmetry. It has an internal structure. One can find 3 twists within this graphical unit. Let's call the twists as a property for the sake of illustrativeness, scent. (This is our name; no such name and property have been applied in physics.) All the three twists, i.e., scents, are left-handed on Figure 1. Scent may take up two values: it can be either left-handed or right-handed. Let's call the left-handed scent 'masculine' and the right-handed scent 'feminine'. The three twists i.e., scents, in the representation of a quark, are perpendicular to each other (like three neighbouring faces of a cube). They form a convex quadratic angle in respect of the plane of the screen. We attribute this convex angle to a 'spin up' state.
Spin of the quarks

Spin up and spin down quarks. There are two quarks represented on Figure 2: spin up and spin down. A spin down quark is represented by a concave graphical unit (like the opposite three neighbouring faces of a cube).


The four possible scent permutations in a graphical unit. All the three twists in the graphical unit of a quark can be left- (L) or right-handed (R). One unite can geometrically consist of 0, 1, 2 or 3 left-handed (i.e., masculine), and 3, 2, 1 or 0 right-handed (i.e., feminine) scents, respectively. No other permutations can be distinguished from each other. All the four permutations of the scents may appear both in spin up and spin down quarks, respectively. For simplicity, later on we will deal only with the spin up states of the quarks.
Colour of the quarks
According to Pauli's principle, in quantum physics no more than two identical fermions (half-spin particles) can take part in a single structural unit (and even those two must be in opposite states). This should be applied also for the scents. Thus the LLL and the RRR (the geometrically most symmetric) graphical units cannot represent real physical particles. There remain two (LRL and RLR) physically possible graphical units. (Due to the rotational symmetry of the graphical unit, LRL, LLR, and RLL permutations are indistinguishable, i.e. identical.) They represent quarks. Nevertheless these two can appear in three different states of a property, called colour, each. Physics named the 3 values of this property as red, yellow and blue. We will represent them by these colours.


Bound (real) quarks
According to our present knowledge and among natural (not-extreme) physical conditions nature produces only bound quarks. Always three quarks form a baryon, and always a quark and an anti-quark form a meson.
When a rotational symmetric quark (or the graphical unit representing it) enters into a binding with two others to form a baryon, it loses its certain symmetries. Note, this is a more general geometric principle of nature, valid not only for the quarks: a single object has more symmetry properties, than as a part of a system. (However, there may appear new symmetry properties in the more complex systems.)
Flavours of the quarks
In the case of our quark model, the binding-clip can be joined to two of the three scents. As one can choose 2 of the 3 scents in three different ways, the number of possible permutations triples. (We get 6 different units, each in 3 colours). Let's make a correspondence between the six colour-triplets and the six quarks in the following way, based on a classification of the clips to which individual scent permutations they join.
| -LRL- | -LRL- | -LRL- | = u (up) |
| -LLR- | -LLR- | -LLR- | = c (charm) |
| -RLL- | -RLL- | -RLL- | = t (top or truth) |

| -RLR- | -RLR- | -RLR- | = d (down) |
| -RRL- | -RRL- | -RRL- | = s (strange) |
| -LRR- | -LRR- | -LRR- | = b (bottom or beauty) |

They join to other quarks graphically by clips connected to two of their constituting units. It is not easy to recognise, therefore we draw the attention, that the 6 quarks differ from each other in the permutation of the Left-handed and the Right-handed twists (masculine and feminine scents) to which their clips are attached. For the sake of easier survey, we represent here each in one colour only.
The physicists call the property of the quarks, that distinguishes them from each other, their flavour. In these terms, one can speak about quarks of the above 6 different flavours (up, charm, truth; down, strange, beauty). Let's assume, that nature prefers their symmetric (i.e., -LRL- and -RLR-) joining, this being the reason for the most frequent appearance of the u and d quarks in the usual matter.
The world is basically built of quarks and leptons. According to our present knowledge, there are among the bricks 6 quarks (and the corresponding 6 anti-quarks). Each of the 6 flavours may be present in 3 colours. Therefore we have altogether 18 quarks (and 18 anti-quarks).
Charge of the quarks
Particles are characterised also by further properties, e.g., electric charge. The charge of the quarks consisting of two masculine and a feminine scent (namely u, c and t) equals to +(2/3) in units of the electron charge. The charge of the quarks consisting of two feminine and a masculine scent (namely d, s and b) equals to -(1/3) in units of the electron charge. Charge can be calculated visually from the scents, as described later.
Baryons
According to our present knowledge, quarks are confined in the hadrons, i.e, we can't experimentally produce single quarks, only their bound states (baryons and mesons). Baryons consist of three quarks, mesons consist of a quark and an anti-quark. Baryons and mesons together are called hadrons. According to our model, if we could watch a hypothetical "single" quark, we could watch it only in two states (not in six) because the permutations of the joining, which distinguish from each other (u , c and t) and (d, s and b) respectively, would vanish in the lack of binding. At the same time, both could appear in all the three colours separately.
The colour of the quarks is not observable. A quark never appears in the nature alone, only in triple or pair. Three quarks form a baryon. (A quark and an anti-quark pair form a meson. They transmit the mutual interchanges, interactions between the baryons.) The quarks within an individual baryon are always of different colour. Moreover, they are changing their colours continually at a very rapid pace. A quark emits a so-called gluon, what another absorbs, and then changes the colour of both. The latter does the same, and changes colour with the third, etc. This mechanism ensures not only the permanent colour change of the individual quarks, but also that all the three have different colours simultaneously. Thus the observer detects always an equal proportion mix of the different colours, therefore the quarks are seen from outside as "white", i.e., colourless.
Any three of the quark flavours may form a baryon. All the constituent quarks are of different (red, yellow and blue) colour. The most usual matter is made of two baryons: protons and neutrons.
Proton
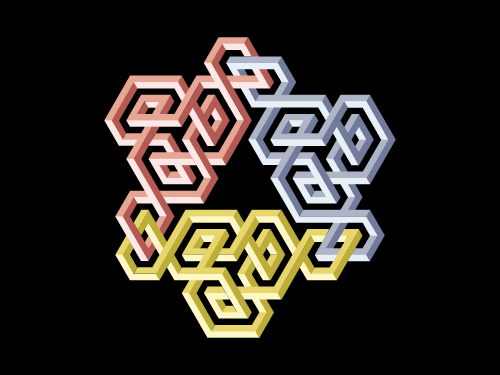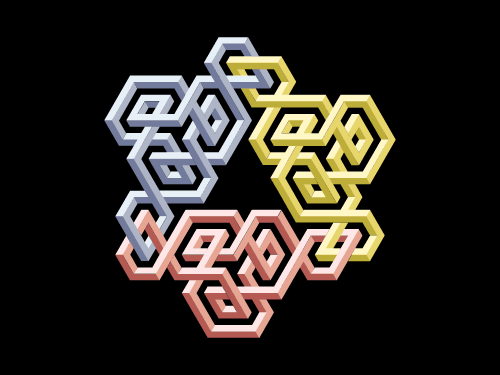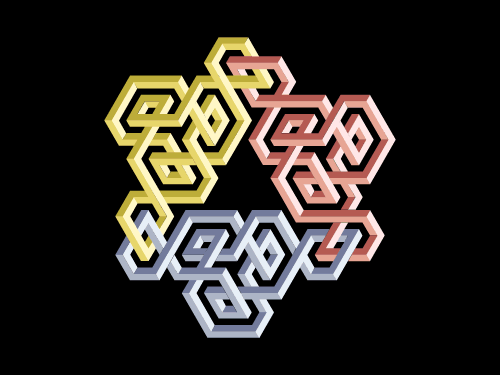
Two u and a d quark are bound to each other in a proton. The colour of the individual quarks on the image is chosen randomly, and all the three change their colours at high frequency. The u and the d quarks within the proton can be distinguished by their binding scents. The u quarks are joined to their partners next to their two Left-handed twists, and the d quark next to its two Right-handed twists. In other words: the u quarks have no joining clip connected to their Right-handed twist, and the d quark has no joining clip connected to its Left-handed twist. (Note, for aesthetic considerations we did not drew a spin-down quark to represent the second u quark.)
Neutron
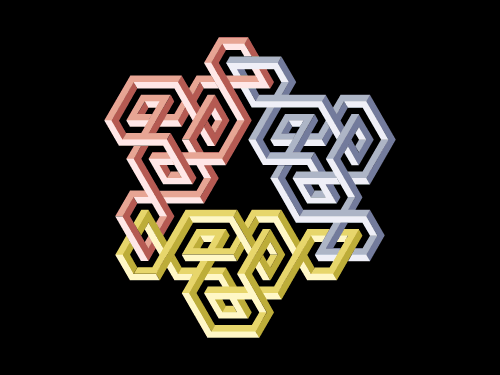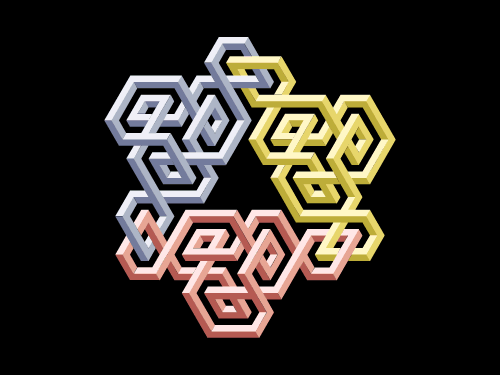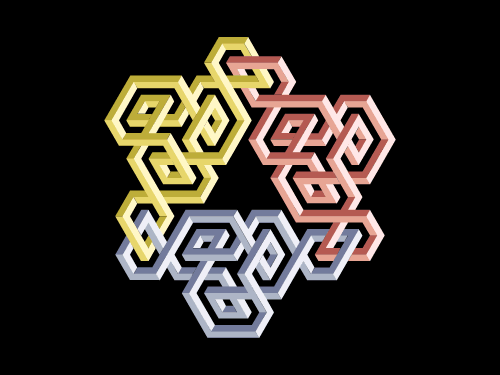
Two d and a u quark are bound to each other in a neutron. The colour of the individual quarks on the image is chosen randomly, and all the three change their colours at high frequency. The u quark is joined to its partners next to its two Left-handed twists, and the d quarks next to their two Right-handed twists. In other words: the u quark has no joining clip connected to its Right-handed twist, and the d quarks have no joining clip connected to their Left-handed twists. (Note, for aesthetic considerations we did not drew a spin-down quark to represent the second d quark.)
Anti-quarks
'Anti'-particle means an opposite sign charge. Anti-quarks have -(2/3) and +(1/3) charge respectively. Anti-quarks are represented in this model by their complementary colours.
In accordance with Quantum Chromodynamics (QCD) anti-quarks are represented (graphically) identical with their corresponding quarks, however, their colour is the complementary colour of the respective quark. (The numerical hexadecimal inverse of a code of a colour determines an inverse-code colour, and this is called the complementary colour of the original.)
Mesons
Mesons are pairs of a quark and an anti-quark.
When forming a meson, quarks are bound only to one other, thus they join to the anti-quarks next to that scent, which does not take part in binding into a baryon. (E.g., a u quark joins to two quarks next to its two Left-handed twists, and to an anti-quark next to its Right-handed twist.)
π+ meson
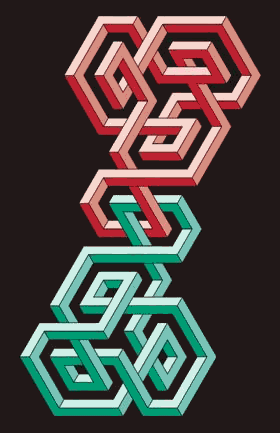
The π+ meson consists of a u and an anti-d (d) quark. The anti-quark is denoted by the complementary colour (green) of the quark's colour (red). A u quark is coupling with another to form a meson joining through its Right-handed twist, while a d or d quark through its Left-handed twist. The charge of a π+ meson equals to +1 (= 2/3 + 1/3).
π- meson
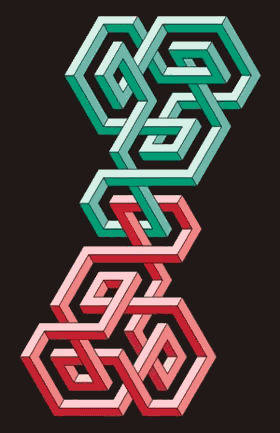
The π- meson consists of an anti-u (u) quark and a d quark. The charge of a π- meson equals to -1 [ = (-1/3) + (-2/3) ].
The process of a baryon transformation
The transformation of a proton into a neutron.
A (p → n + π+) transformation can be graphically described in the following way.
A u quark is drawn out of a proton, while the connecting 'string' is broken (Fig. 12b).
At the broken ends a quark and anti-quark pair (d - d) appears:
- the d quark replaces the u quark in the baryon, thus forming a neutron instead of the former proton, and
- the d quark forms a u-d pair, i.e., a π+ meson, with the u quark (drawn out of the proton) (Fig. 12c).
Note the shift of the joining clip of the u quark from the two L-handed twists when bound in a baryon, to the R-handed twist when bound in a meson, as well as the different joining of the d and the d.

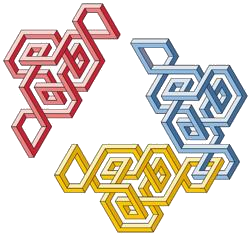
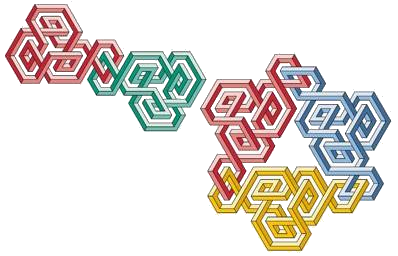
Nuclei
Protons and neutrons form the nuclei of the atoms.
The nucleus of the simplest atom, the Hydrogen, is a single proton. The next simplest nucleus is that of the Deuterium.
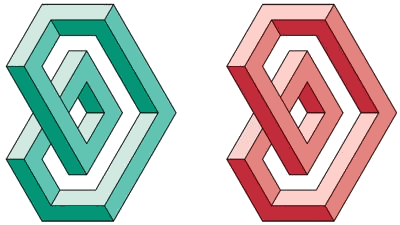
Deuterium
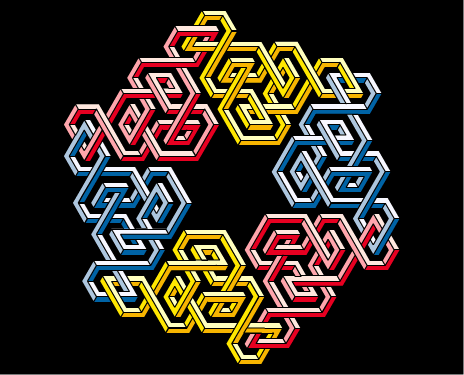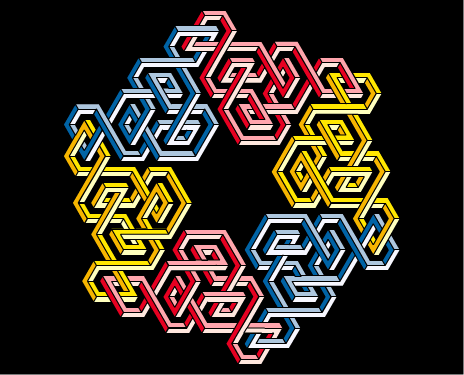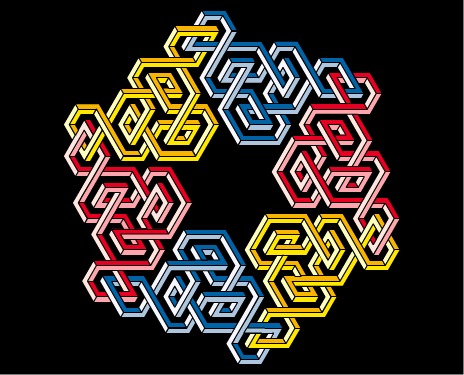
The nucleus of the Deuterium consists of a proton (udu) and a neutron (dud). Thus the nucleus of the Deuterium consists of 3 u and 3 d quarks. Note certain symmetries of the model: both the u and the d quarks appear in all the 3 colours, and the identically coloured quarks appear in opposite spin (convex and concave) states.
A more sophisticated model
Note: The above model can be extended. E.g., we can imagine, that quarks within baryons and nuclei are more intermingled, than shown in the above model, where they could be visually separated.

The applied graphic representation of the quark model makes it possible to represent more complex intermingling of the quarks within a baryon and a nucleon. Although, this representation is capable to represent more detailed physical models, its complexity demands a more sophisticated view on the reader's side. Nevertheless, it demonstrates that the model is open even to further developments of the physical theory.
Rishons
The model can predict properties having not, or only partly assumed in physics. These are assumptions not proven yet. One can observe that the three scents constituting a quark, can be represented as individual units. There is a physical model, introduced by H. Harari in 1978, which set up a hypothesis that all physical particles could be built by the help of two primary components. He called these components rishons. According to Harari's model, there would be two rishons (called by him Tohu and Vohu), with an electric charge (-1/3) and 0 (and the anti-rishons would have the charges 0 and 1/3).
We draw a similar model. However our model paints a bit different picture on the rishons, than Harari's one. We compose the quarks of the two rishons (and their anti-rishons) as represented in Figures 15-18, and want to compose the electric charges of the quarks to be (2/3 for u, c, t) and (-1/3 for d, s, b), as they are set in the Standard Model.
Masculine rishons

Feminine rishons


All the represented quarks can be composed of the introduced two graphical units.
Masculine scent is represented by a Left-handed twisted rishon, feminine scent is represented by a Right-handed twisted rishon.
The u, c, and t quarks (charge +2/3) are composed of two Left-handed twists and a Right-handed twist, or two masculine and a feminine scent rishons.
The d, s and b quarks (charge -1/3) are composed of
two Right-handed twists and a Left-handed twist, or in other words,
two feminine and a masculine scent rishons.
This combination demands, that the electric charge of the masculine scent rishon be +5/9, and the electric charge of the feminine-scent rishon be -4/9.
Observe that these graphical units are asymmetric, each. Their peculiarity is, that one can compose visually symmetric units (quarks, see Figures 1 and 2) from three, individually asymmetric components (rishons). This asymmetry predicted, that one could not expect symmetric properties devoted to these primary components (cf., their electric charges +5/9 and -4/9 respectively).
Leptons
Our rishon model is suitable to represent leptons as well. Let's represent the members of the electron family by red and anti-red (green) colours.
Electron

An electron can be composed of a feminine and an anti-masculine scent rishon (RL).
Its charge is -1 [ = (-5/9) + (-4/9) ]
Positron

A positron can be made of a masculine and an anti-feminine scent rishon (RL).
Its charge is +1 [ = 4/9 + 5/9 ]
Neutrino

A neutrino can be composed of a feminine and anti-feminine scent rishon pair (RR). Its charge is 0.
Anti-neutrino

Similarly, an anti-neutrino can be made of a masculine and anti-masculine rishon pair (LL). Its charge is also 0.
Like Harari's theory, this model can also not give an account of the masses of the leptons. As concerns the colours, quarks can be made only of equal (or in the case of the leptons complementary) colour rishons (the model cannot explain the reasons). This method properly represents the leptons colourless. Maybe the muon and tau lepton families could be represented by the other two colours (yellow and blue) and their complementary colours(?).
Reprinted from http://members.iif.hu/visontay/ponticulus/rovatok/hidverok/QCD-symmetry.html.
