Adventures with Impossible Figures

In this chapter we deal with a new class of impossible figures, where the principle is rather different from anything which has gone before.

Is the candlestick drawn below a sketch of a candlestick which could really exist?

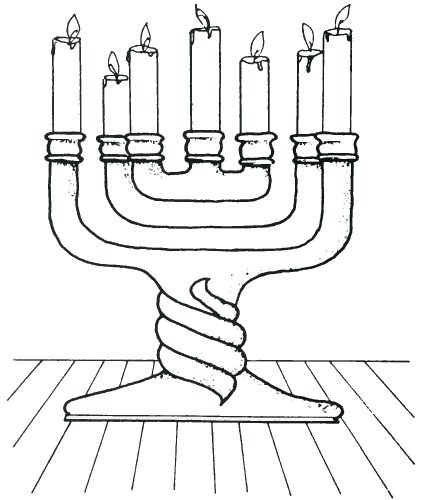
When you look carefully at this candlestick, I am sure that you will agree that in certain places it seems to dissolve away to nothing. Where did the holder of the second candle from the right go to? And the second from the left?

Let us now see what we can find which behaves in a similar and impossible way.

Disappearing blocks

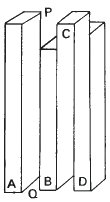
This figure has a strong sense of solidity about it. Both at the bottom and at the top there appear to be three solid blocks. Yet there are problems. Block B undoubtedly exists at the bottom, but as we raise our eyes it just vanishes into nothingness. Block C exists at the top, but it vanishes lower down.

Block A appears to be normal and block D is a variation on the ideas of chapter 8. It is on B and C that we must concentrate.

What then is the trick of the vanishing blocks based on? Let us look at the line PQ. It serves a double function. It is the edge of both block A and of block B. Real objects have real boundaries and that is what we expect to see. Our eye does not have to see a complete outline before starting to interpret it as a solid object. Near to the letter Q the outline of B suggests a solid block. By the time we reach P it has disappeared and that is what causes the shock.

This modified sketch completes the outlines of block B and so the sense of vanishing into thin air has also disappeared. However, other kinds of impossibility still remain to tease the imagination!

Dual-purpose Outlines

The eye automatically uses the outlines of figures to acquire information about planes and their orientation in space. Where the same outline apparently belongs to two different objects, then there can be deliberate confusion. However, the strong sense of confusion that a dual-purpose outline can create is not confined to three-dimensional impossible figures.

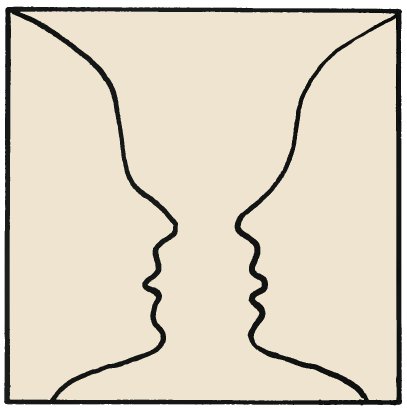
This well-known two-dimensional figure allows two quite different interpretations. Is it a vase, or is it two faces facing each other? It is not an impossible figure, but is closer to the phenomenon of perceptual inversion of chapter 4. It is either a vase or it is a pair of faces. Not both.

Things are not Always What They Seem

The technique of the disappearing outline is one which can produce a whole range of interesting impossible drawings. On the pages which follow we show just a few ideas.

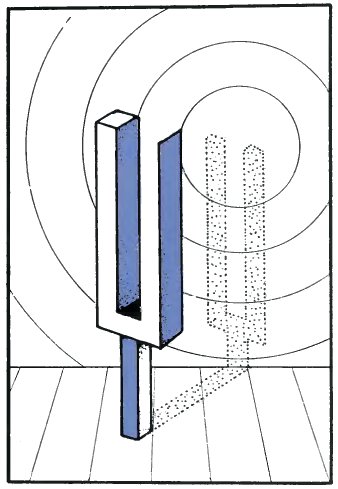
This impossible tuning fork seems to cast a real shadow on the back wall. And of course it is the shadow, not the fork, which emits the soundless sound waves!

Disappearing ink is supposedly much beloved by spies and crooked business men. Are these the first disappearing pencils for artists to use to create invisible masterpieces? Were they used to draw the three pictures on the walls of the art gallery on page 22?

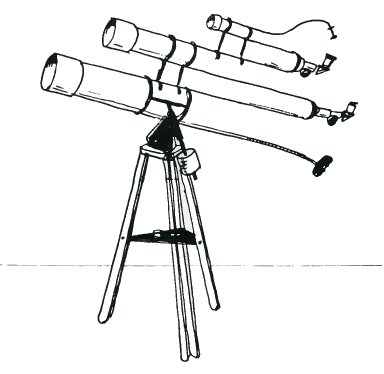
Astronomers often use a small 'finder' scope to point a powerful telescope at a faint object in the night sky. Could the telescope drawn here by Govert Schilling be used to give a clear view of something totally invisible?

"The difficult we do immediately. The impossible takes a little longer". However, the provision of accurate blue-prints does speed up the process!

Is it possible that this Meccano enthusiast has a screw loose?

Things are indeed not always what they seem!