M.C.Escher's Legacy. A Centennial Celebration
Painting after M.C. Escher
My title has dual significance : painting "after", or "from" Escher, and painting "as" Escher.
At the outset, it should clearly be pointed out that M.C.Escher did not make any paintings during his professional career as an artist. His complete works are limited to drawings and prints - lithos, woodcuts and wood engravings, some rare etchings, and a few that use other printing techniques. Although there were some commissioned designs for public buildings that involved painting panels or walls, paintings, by which I mean artworks designed and painted on canvas, panel, or paper, simply do not exist. That does not mean, however, that M.C. Escher hasn't influenced artists in general or any painter in particular.
In light of these observations, "painting as Escher" isn't really an appropriate theme for my essay. So how about painting "after" or "from" Escher?
After having observed all the adapters of Escher I know, I find that there are few painters among them. Artists working with paint on canvas or panel seem to practise almost exclusively the pure non-figurative genre. I believe (if I'm not mistaken) this kind of art would not have been appreciated by Escher. I'm even convinced of the fact that if the meticulous Escher had ever painted, his technique would certainly have had similarities with mine. Carelessness in brush technique, neglecting details, negligent composition of materials, erroneous usage of colors - these would never have ocurred in the hypothetical works of Escher. (Although I've heard or read somewhere that Escher was partly color-blind!)
Lacking directly comparable paintings, I decided to search for basic figures that Escher and his followers used when composing 'impossible pictures'. I purposely use the term "composing" here. Neither the works of Escher nor his followers are thrown impulsively on canvas. Thinking through the composition thoroughly and trying it out in several preliminary studies are indispensable ingredients in the birth of an Escherian work.
The potential for making 'impossible' pictures is limited: they depend on fairly rare geometric configurations. Escher (and others) borrowed most of the basic figures from others, reworking them into concrete, figurative forms. This is where we touch on the thorny problem of the boundary between exact (theoretical) science and art. Or to put it as a question: when does a scientific model become art? The solution to this problem I leave to specialized art critics but I would certainly like to point out that few (or perhaps no) scientific theorists have ever produced art of quality.
By now I think it has become clear to you, respected reader, that my essay is restricted to impossible figures or impossible constructions. However, my introduction to the works of Escher had nothing to do with impossible figures.
The Path to Painting Impossible Figures
In 1956, in the Museum of Applied Art in Ghent (Belgium), I saw a series of Escher's prints. Among them were Dewdrop, Rippled Surface, and Puddle, which made a deep impression on me (Fig. 1; [1, cat. no. 367]). Reflecting the attitude of official art authorities towards Escher's work, this first and only exhibition of M.C. Escher in Ghent was not shown in the Museum for Fine Art, but in the Museum for Ornamental or Applied Art.

At that time, design (of furniture) was still my main occupation. I also held a strong, rather theoretical, interest in painting and sculpture. Three years later, in 1959, I read the famous Penrose's article in the British Journal of Psychology, in which they exhibited the impossible tribar and other impossible constructions. This first contribution about impossible figures would later become an important influence in my decision to exchange interior architecture and design for the risky profession of a painter.
As a lecturer at the Royal Academy of Fine Arts and later at the Higher Institute for Architecture, I was, apart from being a teacher of interior architecture and furniture design, also responsible for classes on the theory of color and on design technique. The mathematical basis of harmony of forms in art was always in the forefront of these subjects. The possible applications of Fibonacci series, the Golden Ratio, and other mathematical-aesthetical systems were discussed in this course, organised as a discussion-forum. We focused especially on the Swiss group of "Concrete Kunst:" Max Bill, Karl Gestner, and Richard P. Lohse (see [4]).
It was also there that I began to take an interest in the boundary between art and science. Several antipodal ideas arise in the search for this difficult limit:
- picturesque versus pictural (or the colorful scene versus the art of painting)
- the means versus the objective
- the basic scheme versus the result
- the technique versus the art
- mathematical art or artistic mathematics.
(See [8] and [9].)
When I decided in 1968 to leave interior architecture and design for the free art of painting, I wanted to depict things that can only exist as "picture". What I was going to depict in my drawings and paintings had to be infeasible or unrealizable. So I inevitably arrived at Impossible Figures. This was probably a reaction to my previous compelling duty to always draw things that techniquely and spatially had to be 'correct', 'measurable', and 'realisable'.
A first basic scheme was the famous dual stairs (Fig. 2) of which I drew and painted a series of variations for a whole year (Fig. 4). The next step was the Thiéry figure of 1895, some variations of which are reproduced in Fig. 5. A typical application of the Thiéry figure is at the right of Fig. 6: my 1972 Ode to architect J. Hoffmann number 10/38.

The Escher lithograph Convex and Concave (Fig. 3) plays with the dual stairs and the kind of Thiéry figure that is reproduced on the flag at top right in the print. Escher explained this convex/concave dichotomy in a letter to his son Arthur in 1954:
Convex and Concave ... is concerned with the widely known phenomenon of spatial suggestion which can be imagined as convex or concave, as desired. In the middle of the picture I draw the shapes in such a way that the observer may just as well see them convex as concave; to the right I force him to see things in a convex way (e.g. "cube from the outside"; to the left, he has to view things in a concave way ("cube from the inside"). [1, p. 79]

On further consideration, one could suggest that the Thiéry figure in perspective was used as a starting point for the 1947 Escher lithograph Up and Down. The small floor a little above the middle of the picture is the double-use surface in the Thiéry figure; here it is simultaneously a floor or ceiling.

All the works from the early years of my painting career are abstract and very often reversible, both horizontally and vertically. Later I made more realistic reproductions, still with the abstract "things" but now resting on firmer ground. The base component from that period is the impossible cube, which also appears frequently later on. In Escher's vignette Man with Cuboid, this cube is not completely impossible. It still shows two normal faces - the bottom and the top (Fig. 6a).

Around 1975 I drew several new versions of the cube in which all the surfaces were impossible. And even better: there are no longer any real clear-cut surfaces. All the aspects of the cube flow into one another. It could be described as a Möbius strip in the form of a cube (Figs. 6b and 7). I'm probably not the inventor of this fully impossible version, but in 1975 I was aware only of Escher's drawing and interpretation.

Eschers Influence
There are only a few prints by Escher that can be related directly to my works. The most important is Belvedere for which the impossible cube served as a starting point (Fig. 8). The small man on the bench contemplating the absurd cube in his hands, as well as the sketch in the foreground on which the ribs of a cube are drawn with their hazardous crossings, are the keys to understanding this enigmatic construction.

Closely related to the impossible cube is the normal cube with impossible connections (Fig. 9a). I'm not acquainted with any works of Escher based on this impossible figure. That's why two of my works reproduced here give reference to other artists (Figs. 9b and 9c).

(b) Souvenir of Margriet, 1977. Acrylic on canvas.
(c) Rather Illogical Architecture - Surrounds for a Very Logical Figure of Max Bill, 1998. Drawing
Apart from the impossible cube we can also make the impossible square and the impossible rectangle (Figs. 10a, 10b). As far as I know Escher used neither of these figures in his works. Some of my works utilize this motif, appearing in several variations, frontally as well as in perspective (Fig. 11).
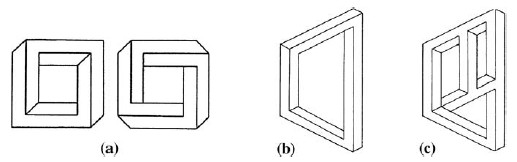
(b) An impossible four-beam figure with a perspective effect.
(c) An impossible four-beam figure with impossible connections
We have seen that apart from the completely impossible cube there can exist also a possible cube with impossible connections. That is also true for the impossible rectangle where a possible rectangle with impossible connections can be devised (Fig. 10c).

Finally there is the impossible triangle of the Penroses, already mentioned above, and also a little bit from Oscar Reutersvärd. Escher used this feigned triangle as a starting point for his 1961 lithograph Waterfall. The great number of preliminary studies [3, p. 89] show the long and difficult process Escher went through before he finally obtained a clear image of his idea. My own drawings based on the impossible triangle (Fig. 12) are much more simple than Escher's intricate picture.

RIGHT: A Latent Threat for an Unstable Construction, 1995. Ink drawings
To make the series of basic figures complete I would like tomention so-called "multiple surfaces". That term was invented by Bruno Ernst (Hans de Rijk) to be able to interpret my works better [2]. He states "a multiple surface looks in a certain place in a drawing or painting like only one flat surface; put in another place in that same picture it is like two or more flat surfaces. This is the oldest type of impossible figure (i.f.) that was , often unintentionally and unconsciously, put into the pictures". [2, p. 62]
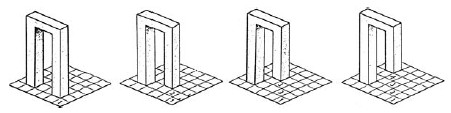
In Fig. 13, you can see Ernst's depiction of how this can originate. In my ink drawing of 1983 (Fig. 14) there is only one surface on the upper part of the wall. This surface multiplies itself on the ground to four walls that stand at different distances from the viewer and that enclose a rather large space like a summerhouse.

My last two illustrations (Fig. 15) give a glimpse of my design technique.
These drawings show how, beginning with a scheme of Reutersvärd, I finally reach an apparently possible pictural figure by reversing, broadening, and narrowing, then finally by using perspective with the viewing angle that of a standing person's eye. That final figure could be used as a basis for a painting or an elaborated drawing.

Some Final Thoughts
It is probably useful at this point to quote Escher himself, "Always try to do that which seems too difficult for you; try to exceed your supposed limits". (from a letter to his son George on June 29, 1969) [10]. Escher always wanted to do just that: what was, in fact, too difficult. Was it ambition? Yes, but not primarily that. It was a typical inner passion that is so characteristic of the real artist. His willpower, his stubborn perseverance and his enormous skill made it possible for him to convert visionary images into clear images. It was often at the expense of sleepless nights and eternal experimenting in order to finally achieve the fragile balance between inner rest and creative expression. He was looking for balance but always preserving emotions.
Escher also always tried to bridge the opposition between abstract and figurative. His works (and also mine) are figurative in form but abstract in meaning. In other words: a figurative representation of abstract ideas.
In a lecture in Amsterdam in 1963 he explained that subtlety is also necessary. "In my opinion an impossible situation only really stands out when the impossibility is not immediately obvious... There should be a certain mysteriousness that does not immediately hit the eye". [1, p. 147]
The link between Escher and the scientific world was his insatiable urge to know everything. In this he resembled what a scientific investigator should be. Escher and his adapters belong to the category of "thinking artists" such as many great artists before them were and many still are. These are artists who investigate systematically the surounding world in an artistic-methodical way. The strong need for studying the phenomenon of human perception is another characteristic that Escher and his followers have in common. In this, they put the liability of that perception in perspective.
Without M.C. Escher, my works as well as those of many other artists would certainly have been completely different. Nevertheless I think I can say that I have been using enough different pictural elements and techniques to distinguish my paintings clearly from the works of Escher. My intention is to elaborate his ideas, using new approaches and a more painted elaboration. The architecture, the scene, the figuration, and the application of colors in my works are strongly related to my own Flemish present and past. It is striking that Escher rarely made use of Dutch scenery. Apart from Day and Night with its bird's-eye view of a typical Dutch landscape, his architecture, scenery, and figuration are almost exclusively southern, and in particular, more Italianesque.
I especially try to respect Escher's attitude towards art. His searching for exactitude and the best possible technical quality when conceiving and realising his works have always been an example for me. I also want to express my gratitude to Bruno Ernst who has often helped me with his analytical understanding and comments on the things that I instinctively put on paper or canvas. I also want to emphasize strongly that I am not, even less than Escher was, a practitioner of exact science. If I was, I would never make any art, even less paint...
Fortunately there are scientists who are interested in art. Science can, to a certain extent, be considered as art. I see myself as an artist with a certain interest in science. I'm probably a scientific artist but I'm certainly not an artistic scientist.
References
- F.H. Bool, J.R. Kist, J.L. Locher, F. Wierda, M.C. Escher, His Life and Complete Graphic Work, Harry Abrams, 1982.
- Bruno Ernst, The Eye Beguiled, B. Taschen Verlag Köln 1992.
- Bruno Ernst, The Magic Mirror of M.C. Escher, Ballantine Books, New York, 1976. Reprint, Taschen-America, 1994.
- Karl Gerstner, Kalte Kunst, Niggli Verlag Schweiz 1957.
- E.H. Gombrich, Art and illusion, Phaidon Press London 1959, Pantheon New York, 1961.
- J.L. Locher, ed., The World of M.C. Escher, Harry Abrams New York 1972.
- L.J. Penrose and R. Penrose, "Impossible Objects: A special type of illusion", British Journal of Psychology, v. 49 (1958) 31.
- Andreas Speiser, Die Mathematische Denkweise, Birkhauser Verlag Basel 1952.
- Hermann Weyl, Symmetry, Princeton University Press, 1952.
- Unpublished materials in the Escher archive, Haags Gemeentemuseum, Holland.
