Möbius strip
 A Möbius strip made with a piece of paper and tape. |
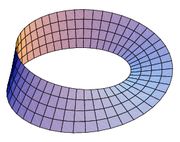
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. It has the mathematical property of being non-orientable. It is also a ruled surface. It was co-discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.
A model can easily be created by taking a paper strip and giving it a half-twist, and then merging the ends of the strip together to form a single strip. A line drawn starting from the seam down the middle will meet back at the seam but at the "other side". If continued the line will meet the starting point and will double the length of the original strip of paper. This single contiguous curve demonstrates that the Möbius strip has only one boundary.
In Euclidean space there are in fact two types of Möbius strips depending on the direction of the half-twist: clockwise and counterclockwise.
Geometry and mathematics
 A parametric plot of a Möbius strip |
Möbius strip can be represented as system of equations using parametrization:
![]()
![]()
![]()
where ![]() and
and ![]() .
This creates a Möbius strip of width 1 whose center circle has radius 1, lies
in the x-y plane and is centered at (0,0,0). The parameter u
runs around the strip while v moves from one edge to the other.
.
This creates a Möbius strip of width 1 whose center circle has radius 1, lies
in the x-y plane and is centered at (0,0,0). The parameter u
runs around the strip while v moves from one edge to the other.
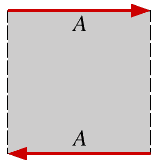 To turn a rectangle into a Möbius strip, join the edges labelled A so that the directions of the arrows match. |
In other way, it can by represented in cylindrical polar coordinates:
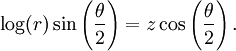
Topologically, the Möbius strip can be defined as the square [0,1] x [0,1] with its top and bottom sides identified by the relation (x,0) ~ (1-x,1) for 0 ≤ x ≤ 1, as in the diagram on the right.
Related objects
A closely related 'strange' geometrical object is the Klein bottle. A Klein bottle can be produced by gluing two Möbius strips together along their edges; this cannot be done in ordinary three-dimensional Euclidean space without creating self-intersections.
One of the basic impossible figures impossible triangle can be represented as Möbius strip if smooth some some edges of the triangle. If a line is traced around the impossible triangle, a 3-loop Möbius strip is formed.
Art
 The international symbol for recycling is a Möbius loop. |
 The Power Architecture logo in the shape of a Möbius strip. |
The Möbius strip has provided inspiration both for sculptures and for graphical art. The artist M.C. Escher was especially fond of it and based several of his lithographs on it. One famous example, Möbius Strip II, features ants crawling around the surface of a Möbius strip (see it in "Mathematical art of M.C. Escher").
It frequently being used in various logotypes and trademarks. The international symbol for recycling is the most known of them.
Appendix. Artistic examples of Möbius Strip
The image below is "Celtic Möbius" by Paul Bielaczyc. It's a marriage of various aspects of author's life. As author says celtic knots surround him at his job, M.C. Escher has always inspired him in his art and the Móbius strip releates to his education.
 Celtic Möbius |
