Klein Bottle
 A Klein bottle modelled in mathematical program |
In mathematics, the Klein bottle is a certain non-orientable surface with no distinction between the "inside" and "outside" surfaces. The Klein bottle was first described in 1882 by the German mathematician Felix Klein. It is closely related to the Möbius strip. The initial name given was "Klein Fla-e-che" (Fläche = Surface). However, this was wrongfully interpreted as Fla-s-che, which ultimately, due to the dominance of the English language in science, led to the adoption of this term in the German language, too.
Picture a bottle with a hole in the bottom. Now extend the neck. Curve the neck back on itself, insert it through the side of the bottle without touching the surface (an act which is impossible in three-dimensional space), and extend the neck down inside the bottle until it joins the hole in the bottom. A true Klein bottle in four dimensions does not intersect itself where it crosses the side.
Unlike a drinking glass, this object has no "rim" where the surface stops abruptly. Unlike a balloon, a fly can go from the outside to the inside without passing through the surface (so there isn't really an "outside" and "inside").
Mathematics
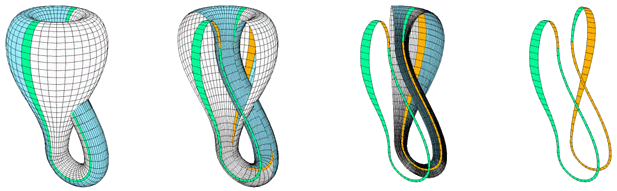
 The "figure 8" immersion of the Klein bottle. |
The Figure-8 surface shown on the right has an even simpler parameterization than the standard Klein bottle.
![]()
![]()
![]()
 |
In this immersion, the self-intersection circle is a geometric circle in the XY plane. The positive constant r is the radius of this circle. The parameter u gives the angle in the XY plane, and v specifies the position around the 8-shaped cross section.
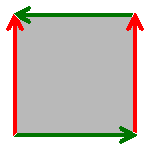
Topologically, the Klein bottle can be defined as the square [0,1] x [0,1] with sides identified by the relations (0,y) ~ (1,y) for 0 ≤ y ≤ 1 and (x,0) ~ (1-x,1) for 0 ≤ x ≤ 1, as in the diagram on the left.
Properties
If we dissecting a Klein bottle into halves along its plane of symmetry we get two mirror image Möbius strips, the one with a left-handed half-twist and the other with a right-handed half-twist. In fact, it is also possible to cut the Klein bottle into a single Möbius strip.
Otherwise, a Klein bottle can be represented as two Möbius bands connected by an ordinary two-sided band whose back and front sides are colored white and blue respectively as you can see at the image below.
 |
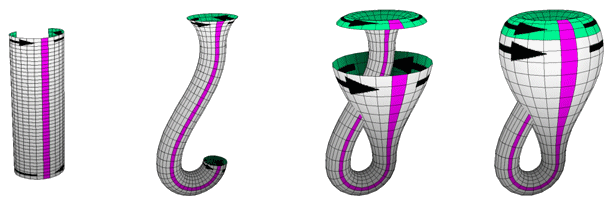
Klein bottle can be constructed from single cylinder. We loop one end back through the cylinder and glue it to the other end, with the two boundary circles given opposite orientations. To accomplish this with a pleasing shape we adjust the thickness of the cylinder. This allows us to glue inside to outside, and obtain a one-sided surface. In the diagram below we have used white and green to distinguish the two sides of the original cylinder. When the Klein bottle is finished, the colors still show where the cylinder was glued together, but gluing at any other parallel circle would have been just as good.
 |
The article was created by matherials of Wikipedia and "Imaging maths - Inside the Klein bottle" by Konrad Polthier
