Фракталы
Cameron Browne
Некоторые части базовых невозможных фигур могут быть вырезаны и заменены частями той же фигуры, получая таким образом новую невозможную фигуры. Затем эту процедуру можно повторить над новой, вырезая из только вставленных элементов части и меняя их на другие. Повторяя эти операции несколько раз можно получить невозможную фигуру, обладающую свойством самоподобия, характерную для фракталов
Ниже показаны фрактальные невозможные
фигуры, созданные Камероном Брауном (Cameron Browne).
http://members.optusnet.com.au/digex/impossible-fractals-figures/

Рис. 1. Невозможный треугольник, снежинка Коха и треугольник Серпинского.

Рис. 2. Две итерации, произведенные над невозможным треугольником, превращающим его в снежинку.

Рис. 3. Альтернативный вариант создания снежинки с сохранением формы треугольника.
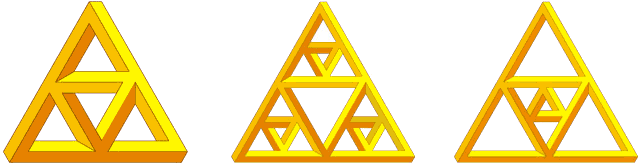
Рис. 4. Создание фигуры по образу треугольника Серпинского.
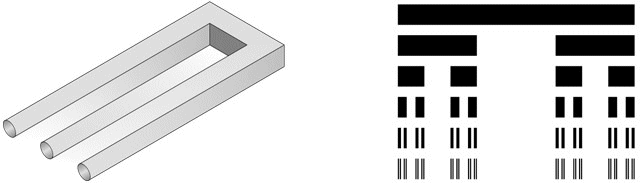
Рис. 5. Вилка дьявола (невозможный трезубец) и множество Кантора.
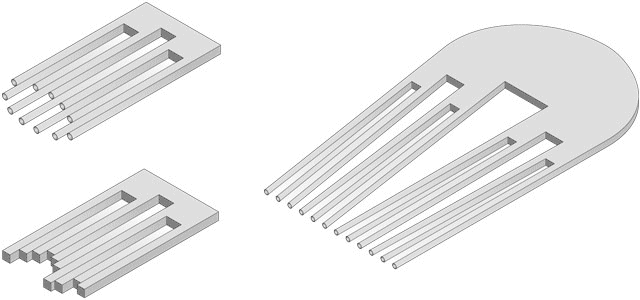
Рис. 6. Две фигуры слева представляют собой прообраз множества Кантора второго порядка в виде невозможной фигуры. Фигура слева представляет то же множество третьего порядка.

Рис. 7. Два невозможных квадрата были использованы для создание невозможной кривой Серпинского.

Рис. 8. Невозможный ящик и губка Менгера после одной и трех итераций.

Рис. 9. Наборы кубов и куб Моники Буш.
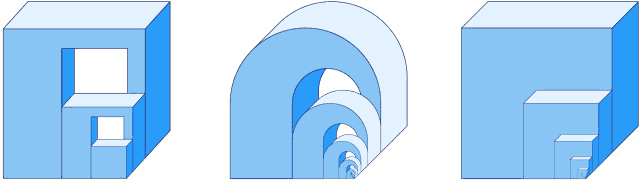
Рис. 10. "Гнездо невозможных кубов" Бруно Эрнста и две его вариации.

Рис. 11. Кривая Пеано-Госпера в виде невозможного много-балочника.

Рис. 12. "Меандр" Реутерсварда и меандр Гильберта.
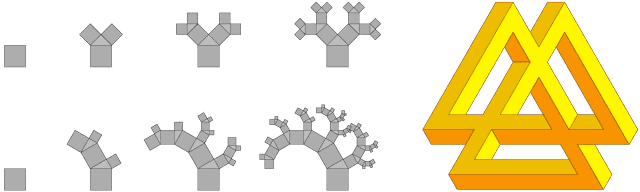
Рис. 13. Пифагорово дерево с углом разворота 45°, сбалансированное дерево с углом разворота 30° и сложный невозможный треугольник.

Рис. 14. Невозможный гриб (Пифагорово дерево с углом разворота 45°).
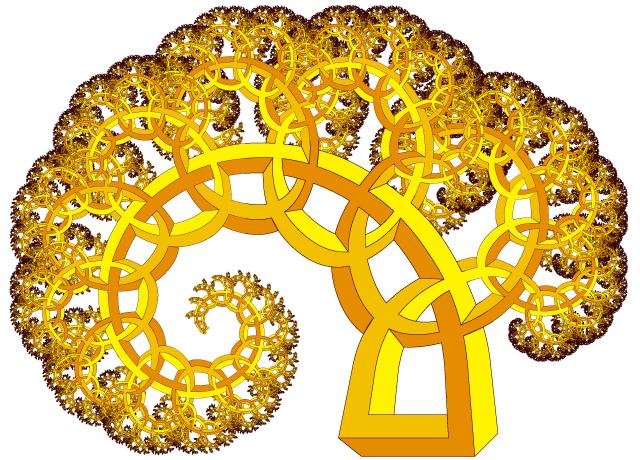
Рис. 15. Невозможный лист папоротника (сбалансированное пифагорово дерево с углом разворота 30°).
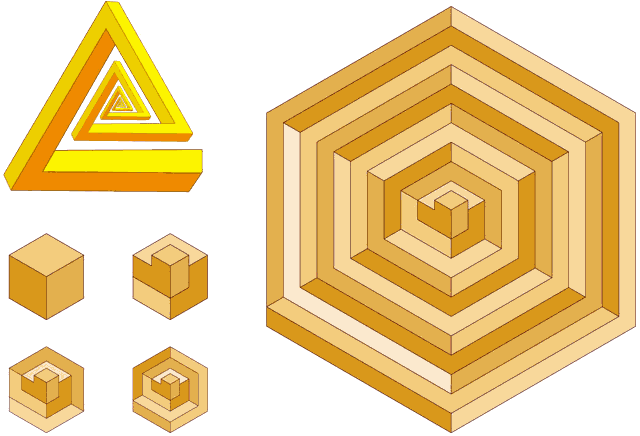
Рис. 16. Спиралевидный треугольник и шестиугольные изометрические спирали.
