Анимация невозможных объектов
Chih W. Khoh и Peter Kovesi
Аннотация
Трехмерные модели невозможных объектов выглядят невозможными только с одного угла обзора. С других углов они уже не выглядят невозможными. Но возможно ли создать интерактивный невозможный объект, выглядящий невозможным с любого угла обзора? Эта статья исследует создание таких объектов на компьютере. Чтобы невозможный объект выглядел невозможным с любого угла обзора необходимо, чтобы его геометрия изменялась таким образом, чтобы с новой точки обзора объект снова выглядел невозможным. Мы покажем, что один некоторые классы невозможных фигур могут быть представлены в виде двух взаимодополняющих частей. Взаимодополняющие части связаны друг с другом обратным преобразованием координат относительно плоскости изображения. Они также связаны принципом обратного отображения поверхностей. Каждая из взаимодополняющих частей может быть реализована как трехмерный объект таким образом, чтобы вместе они образовывали невозможный объект. Трехмерная модель одной из взаимодополняющих частей может анимироваться стандартными способами. При изменении точка обзора, взаимодополняющие части должны быть реконструированы обратным преобразованием для того, чтобы снова получилась невозможная фигура.
Введение
Невозможная фигура определяется как двухмерное изображение, воспринимаемое таким образом, что у зрителя создается впечатление, что подобного трехмерного объекта не может существовать в реальном мире. Ключевые слова в данном определении - "впечатление" и "восприятие". Невозможная фигура на первый взгляд должна производить впечатление обычного трехмерного объекта, но при внимательном рассмотрении фигуры у человека складывается впечатление, что такой фигуры не может существовать в реальном мире. Кроме того, свойство "невозможности" не просто свойство рисунка, а особенность пространственного восприятия человеком нарисованного объекта [9].
Однако во многих случаях возможно построить трехмерную модель невозможной фигуры. Эта модель не будет соответствовать нормальному восприятию фигуры человеком. Как правило, трехмерная модель невозможной фигуры должна рассматриваться с какого-то определенного угла обзора, чтобы возникла иллюзия невозможности. Например, трехмерная модель картины М. К. Эшера "Бельведер" ("Belvedere") [3,10] была построена японским художником Шигео Фукудой (Shigeo Fukuda) [2], а модель невозможного треугольника и куба - Мэтью Хемекерсом (Mathieu Hamaekers)[2]. Иллюстрации других моделей могут быть найдены на web-сайте IllusionWorks [5]. Сугихара (Sugihara) [13] описывает интерактивную систему, которая позволяет создавать многогранники из невозможных фигур и рисовать их развернутые поверхности. Обычно все трехмерные модели невозможных фигур содержат множество щелей и изгибов. Однажды увиденные, эти щели и изгибы уничтожают иллюзию невозможности, и модель теряет свое "волшебство" (рис. 1).
Необходимо прояснить различие между терминами "невозможная фигура", "невозможный объект" и "трехмерная модель". Трехмерная модель - это физически представимый объект, при проецировании которого на двухмерную плоскость получается невозможная фигура. Эта невозможная фигура создает впечатление невозможного объекта (в отличие от трехмерной модели), который может существовать только в воображении человека.

Рис. 1. Три вида модели невозможного
прямоугольника. Трехмерная модель состоит из
двух U-образных объектов. Только первый вид
трехмерной модели создает впечатление
невозможной фигуры
Невозможные фигуры создают впечатление трехмерного объекта, и это подразумевает, что такой объект вполне возможно вращать и рассматривать его с различных углов. Однако, при вращении трехмерной модели, которая соответствует невозможной фигуре, сразу же станут видны все щели и изгибы в модели, и иллюзия невозможности будет разрушена. Модель невозможного объекта в таком случае должна быть каким-то образом перестроена, чтобы создать эффект невозможности с другой точки обзора. При изменении точки обзора модель должна быть подстроена к ней. Но при этом мы должны удовлетворить следующим условиям:
- Компоненты фигуры , которые кажутся прямыми с одной точки обзора, должны казаться прямыми со всех точек обзора.
- Компоненты фигуры, которые кажутся связанными с одной точки обзора, должны казаться связанными со всех точек обзора.
Обратите внимание, что движущийся невозможный объект не может выглядеть невозможным со всех точек обзора, но этого вполне достаточно, чтобы представить невозможный объект с некоторых углов. При этом необходимо удовлетворить лишь вышеприведенным условиям.
Мы можем решить эту проблему при помощи компьютерной модели объекта. Компьютер дает способ, который позволяет нам непрерывно изменять трехмерную модель при изменении точки обзора таким образом, что проекция трехмерной модели на плоскость продолжает удовлетворять правилам, делающим фигуру невозможной. Окончательная цель могла бы быть такой: создать невозможный мир, подобно мирам, изображенным Эшером (Escher), таким образом, чтобы люди могли взаимодействовать с ним в условиях виртуальной реальности.
Конструирование невозможных фигур при помощи взаимодополняющих частей
Роджер и Лайноел Пенроузы (Roger Penrose and Lionel Penrose) [11] описывают невозможные фигуры следующим образом: "Каждая отдельная часть фигуры выглядит нормальным трехмерным объектом, но вследствие неправильного соединения частей фигуры восприятие фигуры полностью приводит к иллюзорному эффекту невозможности". Подобной точки зрения придерживался и Хаффман (Huffman)[4], который показал, что в общем случае невозможные фигуры имеют в отдельных областях имеют последовательную, но при рассмотрении всей фигуры, глобально непоследовательную маркировку линий.
Рассмотрим невозможный прямоугольник, показанный на рис. 2. Эта фигура также известна как невозможный четырехугольный тор или невозможный четырехугольник[1,2]. Главная особенность этого невозможной фигуры то, что она может быть разделена на две половины, которые при рассмотрении независимо друг от друга соответствуют глобально последовательным трехмерным объектам и являются "возможными".
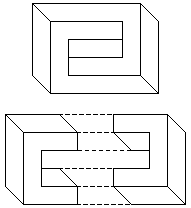
Рис. 2. Невозможный прямоугольник и две
взаимодополняющие части, каждая из которых
глобально последовательна.
Важнейшая особенность этих двух глобально последовательных объектов то, что при проецировании их на плоскость их изображения соединяются без швов, и, таким образом, хотя в локальной области получившаяся фигура последовательна, но при рассмотрении ее целиком видно, что она глобально непоследовательна.
Назовем проекции двух (глобально последовательных) частей объекта, взаимодополняющими частями невозможной фигуры [6]. Взаимодополняющие части связаны друг с другом обратным преобразованием. То есть одна взаимодополняющая часть может быть получена из другой путем двух последовательных отражений относительно ортогональных осей на плоскости изображения.

Рис. 3. Одна взаимодополняющий частей может быть
получена из другой путем отражения относительно
двух ортогональных осей.
Таким образом, прежде чем работать в плоскости изображения, необходимо подумать о создании взаимодополняющих частей в трехмерном пространстве. Если одна из частей проецируется из трехмерного пространства на двухмерную плоскость вдоль оси z, то трехмерную модель второй половины можно построить просто отражая первую половину относительно осей x и y, а координата z останется неизменной. Именно на этом принципе построена модель на рис. 1. Трехмерная модель каждой из взаимодополняющих частей невозможного прямоугольника представляют собой объект U-образной формы. Координаты x и y вершин одной из взаимодополняющих частей равны координатам x и y соответствующих вершин другой части взятым с противоположным знаком. Правильное расположение двухмерных проекций двух частей гарантируется верным выбором направляющей линии, вдоль, которой они расположены. В данном случае направляющая помещена между концами зубцов U-образных объектов.
Другой подход к созданию взаимодополняющих частей состоит в обратном отображении видимых и невидимых поверхностей трехмерной модели взаимодополняющей части. Однако этот подход требует, чтобы невозможный объект, который мы желаем построить, имел очевидный соответствующий реальный объект. Этот процесс лучше проиллюстрировать примером. На рис. 4 показано создание возможного прямоугольника из двух половин. Если мы полностью обратим видимость поверхностей изображения правой части (то есть, сделаем видимые поверхности невидимыми, а невидимые покажем) перед соединением двух половин, то мы получим невозможный прямоугольник. Процесс обращения видимости поверхностей соответствует переключателю восприятия демонстрируемым при помощи куба Некера (Necker Cube) на рис. 5.
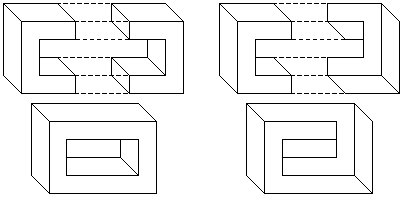
Рис. 4. Невозможный прямоугольник может быть
создан, полностью обращая видимость правой
половины возможного прямоугольника.
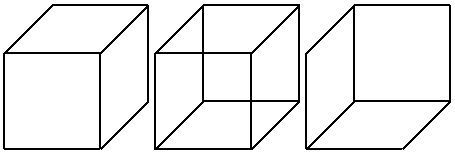
Рис. 5. Куб Некера (в центре) и две его
интерпретации (слева и справа).
Множество невозможных фигур может быть построено при помощи взаимодополняющих частей. В качестве примеров можно привести невозможный тор (пример, показанный на рис. 6 - странный круг Симанека (Simanek) [12]), невозможная кабина (на основе которой создана работа М. К. Эшера (M. C. Escher) "Бельведер" (Belvedere), и сумасшедший куб. Обратите внимание, что создание сумасшедшего куба требует дополнительного шага для решения пересечения линий.
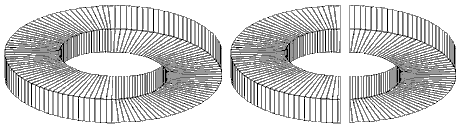
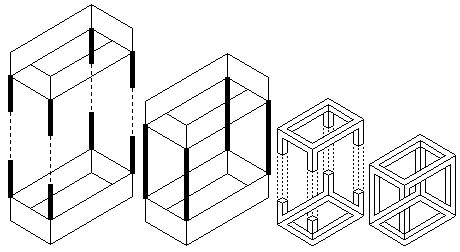
Рис. 6. Создание невозможного тора (вверху),
невозможная кабина (слева) и сумасшедший куб
(справа) при помощи взаимодополняющих частей.
Использование взаимодополняющих частей дает систематический и общий подход к созданию невозможных фигур. Взаимодополняющие части дают сильно различающиеся аспекты объекта. То есть две взаимодополняющие части представляют два вида объекта с очень различающихся точек обзора. Кроме того, по определению, две половины имеют соответствующие число линий для бесшовного соединения друг с другом и создания глобально непоследовательной фигуры. Другие попытки находить систематические подходы к созданию невозможных фигур есть в работах Кована (Cowan) и Эрнста (Ernst) [1,2], которые демонстрируют, как невозможные прямоугольники могут быть построены соединением фиксированного набора угловых элементов. Однако, при использовании этого подхода, получающаяся фигура не всегда производит удовлетворительное впечатление невозможного объекта. Использование взаимодополняющих частей для создания невозможных фигуры более общий способ и дает большую гарантию, что убедительный невозможный объект будет воспринят человеком.
Метод обратного преобразования координат, которое связывает взаимодополняющие части, дает два сильно различающихся вида (или аспекта) фигуры и может иллюстрироваться через граф аспектов [7,8]. Рисунок 7 показывает граф аспектов куба. Каждый узел в графе представляет основной вид или аспект объекта. Аспект объекта - диапазон видов объекта, при которых топология проектируемого изображения остается неизменной. Грани в графе показывают возможные переходы между аспектами. Если мы возьмем аспект куба, который показывает основание и две боковые стороны, и применим обратное преобразование координат (или изменим видимость скрытых и видимых поверхностей), мы построим другой аспект объекта, а расстояние в графе соответствует виду, показывающему вершину и две боковые стороны. Таким образом, слияние двух взаимодополняющих половин может быть выражено в терминах одновременного представления двух отдаленных аспектов объекта в пределах одной фигуры. Это и создает впечатление от невозможности.
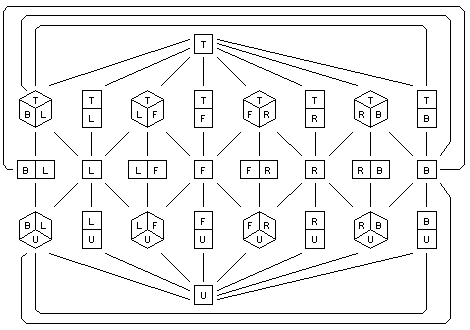
Рис. 7. Граф аспектов куба. Передняя сторона, левая
сторона, правая сторона, задняя сторона, верх и
низ куба обозначены буквами F, L, R, B, T и U
соответственно.
Вращение невозможного прямоугольника
Для создания анимации невозможной фигуры мы должны сначала создать трехмерную модель, которая при проецировании на плоскость выглядит невозможной фигурой. Эта трехмерная модель должна непрерывно изменяться некоторым образом в зависимости от точки обзора так, чтобы впечатление сохранялся эффект невозможности. Одним из подходов к этой проблеме - метод Сугихары (Sugihara) [13]. Но, в методе Сугихары (Sugihara) отправной точкой является невозможная фигура, и когда трехмерная модель для фигуры создана, то не ясно как ее необходимо изменять при смене точки обзора.
Возможность делить невозможную фигуру на взаимодополняющие части значительно упрощает задачу создания трехмерной модели невозможной фигуры. Нам необходимо создать трехмерную модель, которая соответствует одной половине фигуры. Вторая половина получится при помощи обратного преобразования координат. На основе этого можно создать алгоритм для анимации невозможных объектов, составленных из взаимодополняющих частей.
Шаги алгоритма следующие:
- Построить трехмерную модель, представляющую одну глобально последовательную часть невозможного объекта.
- Ориентировать ее соответствующим образом.
- Построить другую взаимодополняющую часть из первой (заметим, что создание второй части является функцией вида первой половины).
- Отобразить соединенные взаимодополняющие части на двухмерной плоскости.
Рис. 8 показывает результаты вращения невозможного прямоугольника. Заштрихованная половина прямоугольника - трехмерная модель, которую мы вращаем, а белая половина прямоугольника - взаимодополняющая часть, построенная на плоскости изображения.
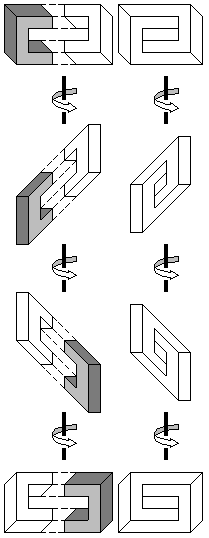
Рис. 8. Вращение невозможного прямоугольника.
Фигуры с левой стороны иллюстрируют процесс, с
помощью которого конструируются фигуры справа.
Анимация требует непрерывной модификации трехмерной модели
Вы, возможно, заметили, что невозможный прямоугольник кажется более тонким на виде со стороны (второе и третье изображения на рис. 8). Это - побочный эффект получения линий каждой из взаимодополняющих частей из-за того, что они должны соединяться друг с другом. В соединении двух половин невозможного прямоугольника верхняя поверхность одной частей должна быть слита с поверхностью боковой стороны зубца другой части. То есть, величины ширины спроецированных верхней и боковой поверхностей должны быть одинаковы, чтобы они стыковались друг с другом (рис. 9). Поскольку объект вращается, толщина проекций поверхностей изменяется. Чтобы компенсировать это, мы должны регулировать толщину трехмерной модели и/или регулировать высоту боковых сторон зубцов так, чтобы ширина проекции верхней поверхности соответствовала ширине проекции боковой стороны. Рис. 10 показывает этот процесс при создании сумасшедшего куба.
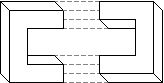
Рис. 9. Без регулировки толщины невозможного
прямоугольника при вращении взаимодополняющие
части не могут быть соединены.
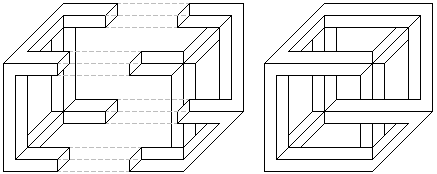
Рис. 10. Чтобы позволить соединиться
взаимодополняющим частям сумасшедшего куба
смежные бруски не должны быть квадратными в
сечении.
Таким образом, мы должны модифицировать наш алгоритм анимации следующим образом:
- Построить трехмерную модель, представляющую одну глобально последовательную половину невозможного объекта.
- Ориентировать ее к требуемому виду.
- Спроецировать на двухмерную плоскость.
- Вычислить толщину проекций смежных поверхностей.
- Вычислить коэффициент масштабирования толщины поверхностей, которые должны соединяться друг с другом
- Изменить толщину соответствующих поверхностей трехмерной модели.
- Учитывая пересмотренные измерения первой взаимодополняющей части, построить вторую часть.
- Отобразить соединенные взаимодополняющие части на плоскости.
Проецирование является линейной операцией. Следовательно, масштабирование поверхностей на двухмерной проекции напрямую связано с масштабированием соответствующих поверхностей трехмерной модели. Следует отметить, что при некоторых углах обзора отдельные поверхности фигуры могут вырождаться. Вследствие чего ширина соответствующих поверхностей трехмерной модели становится равной нулю. При вырождении отдельных поверхностей в линию должен использоваться коэффициент масштабирования равный нулю. Другие виды вырождения возникают при построении концевых видов (вид сверху, сбоку). Примеры таких случаев вырождения можно увидеть на рис. 11.
В целом, использование взаимодополняющих частей для описания невозможных фигур значительно упрощает создание соответствующего невозможного объекта. Постоянная перестройка трехмерной модели при изменении точки обзора сокращена до одной операции: изменения размеров объекта, используемого в модели одной из взаимодополняющих частей. При анимации невозможного прямоугольника этим изменением геометрии является простая настройка толщины и/или высоты соединяющихся зубцов. Эта постоянная настройка трехмерной модели вносит дополнительный аспект в невозможность фигуры.
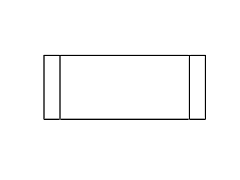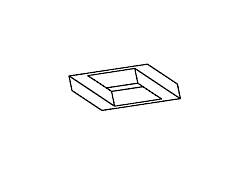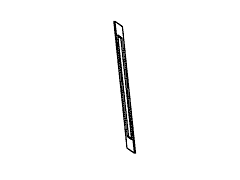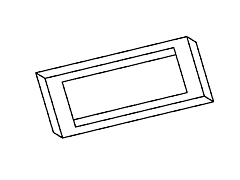
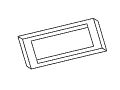
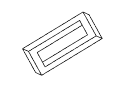
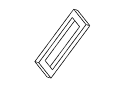
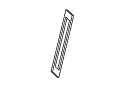
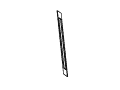
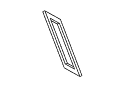
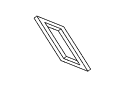
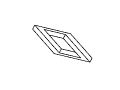
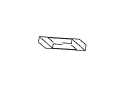
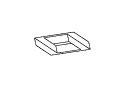
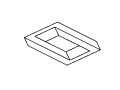
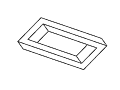
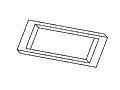

Рис. 11. Полный набор кадров вращения невозможного
прямоугольника. Обратите внимание на случаи
вырождения, которые возникают в тех случаях,
когда объект рассматривается непосредственно
сбоку или сверху.
Заключение
Невозможные фигуры могут анимироваться. Чтобы сделать это необходимо решить две проблемы. Во-первых, создать трехмерную модель фигуры, и, во-вторых, определить каким образом должна изменяться трехмерная модель при изменении точки обзора, чтобы эффект невозможности фигуры оставался.
В данной статье представлена концепция взаимодополняющих частей невозможной фигуры. Показано, как могут быть построены взаимодополняющие части на основе обратного преобразования и обратного отображения поверхностей. Использование взаимодополняющих частей дает систематический способ создания отдельных классов невозможных фигур. Этот подход облегчает создание анимации невозможных фигур, значительно упрощая создание невозможных объектов из соответствующих им невозможных фигур. Только одна взаимодополняющая часть фигуры должна использоваться. Она может быть смоделирована как обычный трехмерный объект. При этом необходима постоянная перестройка трехмерной модели при изменении точки обзора. Эта настройка сокращена до простого пересчета размеров отдельных частей объекта. К тому же постоянная настройка размеров трехмерной модели придает дополнительный эффект невозможности фигуре.
Chih W. Khoh и Peter Kovesi
Университет Западной Австралии
Факультет Информатики
5 февраля 1999
Литература
| [1] | Thaddeus M. Cowan. The theory of braids and the analysis of impossible figures. Journal of Mathematical Psychology, 11:190-212, 1974. |
| [2] | Bruno Ernst. The Eye Beguiled: Optical Illusions. Benedikt Taschen Verlag GmbH, 1992. |
| [3] | M. C. Escher. The Graphic Work of M.C. Escher. Pan/Ballentine, London, 1972. Translated by John E. Brigham |
| [4] | D. A. Huffman. Impossible objects as nonsense sentences. In Bernard Meltzer and Donald Michie, editors, Machine Intelligence, volume 6, pages 295-323. Edinburgh University Press, 22 George Square, Edinburgh, Great Britain, 1971. |
| [5] | IllusionWorks, L.L.C. IllusionWorks Home Page. World Wide Web Site. http://www.illusionworks.com. |
| [6] | Chih W. Khoh. That's Impossible!, 1998. Honours Thesis. Department of Computer Science, The University of Western Australia. |
| [7] | J. J. Koenderink and A. J. van Doorn. The internal representation of solid shape with respect to vision. BioCyber, 32:211-216, 1979. |
| [8] | J. J. Koenderink and A. J. van Doorn. Photometric invariants related to solid shape. Optica Acta, 27(7):981-996, 1980. |
| [9] | Zenon Kulpa. Are impossible figures possible? Signal Processing, 5(3):201-220, May 1983 |
| [10] | Paul Schofield. World of Escher. World Wide Web Site. http://www.worldofescher.com. |
| [11] | L. S. Penrose and R. Penrose. Impossible objects: a special type of visual illusion. British Journal of Psychology, 49(1):31-33, 1958. |
| [12] | Donald E. Simanek. Adding Depth to Illusions. WWW document. http://www.lhup.edu/~dsimanek/3d/illus2.htm, December 1996. |
| [13] | Kokichi Sugihara. Three-dimensional realization of anomalous pictures - an application of picture interpretation theory to toy design. Pattern Recognition, 30(7):1061-1067, July 1997. |
Перевод на русский язык Влад Алексеев
25 июня 2001
Первоисточник находится по адресу
http://www.cs.uwa.edu.au/~pk/Impossible/impossible.html
копия на англоязычной версии
сайта
http://imp-world-r.narod.ru/english/articles/animation/animation.html
