Камерон Браун. Невозможные фракталы
3. Треугольные фракталы
На рис. 1 (по центру и справа) показаны эволюционное развитие двух широко известных фракталов – снежинки Коха и салфетки Серпинского. В снежинке изменяется периметр исходной формы, а в салфетке Серпинского рекурсивно вырезаются внутренние части фигуры.
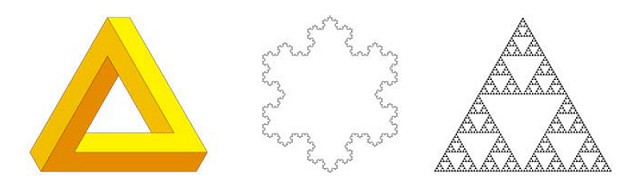
Рис. 2 показывает развитие трибара в вид невозможной снежинки. Первая итерация может быть полностью построена при помощи элементов одного типа, остроугольного генератора (справа сверху), повторенного шесть раз в цикле с соответствующим окрашиванием. Для следующих итераций требуются комбинации остроугольных и тупоугольных генераторов.

На рис. 3 показаны альтернативная версия эволюции снежинки, которая сохраняет родительские треугольники из предыдущих поколений и использует их в качестве основы, на которую последовательно устанавливаются новые распорки. Хотя, этот фрактал не является традиционной снежинкой, а окончательный вид более насыщен деталями, чем предыдущая фигура, этот вариант фрактала требует для построения только один тип генераторов (справа), а распорки повышают неоднозначность перспективы, усиливая эффект невозможности.

В обоих случаях толщина всех брусков фигуры одинаково уменьшается с каждой следующей итерацией для сохранения единообразия фигуры. К сожалению, эффект иллюзии уменьшается с каждой итерацией, так как становится сложнее различать отдельные элементы.
Обратимся теперь к салфетке Серпинского. На рис. 4 показан невозможный объект похожий на салфетку, который может быть получен последовательным копированием трибаров в меньших масштабах. Отметим, что бруски в каждом из трибаров имеют внутреннюю и внешнюю сторону, и у каждого дочернего треугольника цвета сторон должны совпадать с цветами сторон родительского треугольника, с которыми они соединяются. Это правило выполняется для первой итерации, в которой дочерний треугольник соединяется с внешними сторонами родительского треугольника (рис. 4, слева), и для второй итерации, в которой каждый дочерний треугольник соединяется с внутренними сторонами родительского треугольника (рис. 4, посередине). Но для следующих итераций выполнение этого правила раскрашивания становится проблематичным, так как требуется соединить дочерние треугольники с двумя внутренними гранями и одной внешней (или наоборот). Данная проблема не возникает, если в каждой следующей итерации формировать только центральный дочерний треугольник (рис. 4, справа), который остается раскрашенным правильно при любом количестве итераций, однако данный процесс не является стандартным рекурсивным методом построения салфетки Серпинского.

