Камерон Браун. Невозможные фракталы
7. Кривые, заполняющие пространство
В общем случае создать иллюзию с мультибаром возможно для большинства кривых, которые могут быть изображены на изометрической сетке. Например, на рис. 11 показаны три итерации кривой Пеано-Госпера [6], называемой также змеей, реализованной в виде невозможного мультибара.

Аналогично, на рис. 12 (слева сверху) изображен "Меандр" Реутерсварда и его использования в первых трех итерациях в кривой Гильберта, расположенной на изометрической сетке для получения меандра Гильберта. Этот дизайн основан на иллюзии дьявольского трезубца и содержит неоднозначность между фигурой и фоном. Однако еще одна иллюзия не была найдена прежде в оригинальном меандре, которая содержит сразу два эффекта в одном:
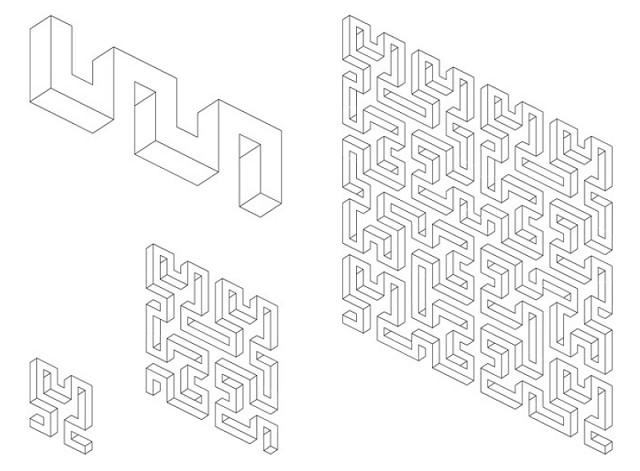
- Неоднозначность фигуры и фона (как дьявольском трезубце). Отметим, то фигура оригинального меандра сливается с фоном только снизу, в то время как меандр Гильберта сливается с фоном с всех четырех сторон без потери эффекта.
- Неоднозначность перспективы (как в мультибарах). Верхняя часть каждой дочерней фигуры Гильберта выглядит выступающей за пределы листа при осмотре справа налево, в то время как нижняя часть выглядит выступающей при осмотре слева направо. При осмотре фигуры вдоль ее контура каждая отдельная часть интерпретируется мозгом, переориентируя представление о фигуре к новой перспективе, забывая предыдущую.
Меандр Гильберта лучше всего изображать в черно-белом виде, как из дьявольский трезубец, так как схемы раскраски мультибаров здесь неприменимы.
