Камерон Браун. Невозможные фракталы
8. Деревья Пифагора
Фракталы на основе мультибаров рассматривались нами так, что они содержали бруски одной и той же тощины на каждом шаге рекурсии. Теперь рассмотрим вариант фрактала, в котором тощина брусков последовательно уменьшается от шага к шагу, что более соответствует природе фракталов.
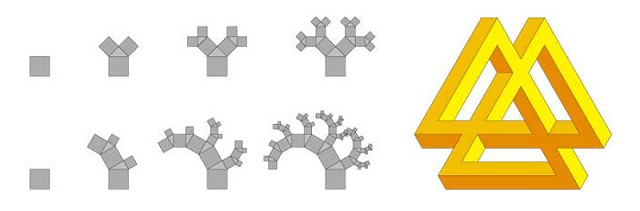
На рис. 13 (слева сверху) показаны первые четыре итерации 45-градусного пифагорова дерева, которое формируется из трех квадратов, касающихся друг друга вершинами, образуя внутри прямоугольный треугольник с двумя углами по 45°. На рис. 13 (слева снизу) показаны первые четыре итерации 30-градусного сбалансированного пифагорова дерева. Данное дерева называется "сбалансированным", потому что левые ответвляющиеся квадраты, которые почти в два раза увеличивают левую ветку, вызывают более сильное развитие в видимых частях дерева, приводя в более однородному распределению деталей. Обычное 30-градусное дерево Пифагора требует для своего построения почти вдвое больше итераций для достижения размеров деталей как у предыдущего дерева, требуя для своего построения большего количества вычислений. 45-градусное пифагорово дере сбалансировано по-определению.

На рис. 13 (справа) изображен расширенная версия трибара, с внешними элементами которого можно работать как с ветвями наподобие дерева Пифагора. Рис. 14 демонстрирует расширенный трибар адаптированный к форме 45-градусного пифагорова дерева после пятнадцати итераций. На рис. 15 расширенный трибар адаптирован для 30-градусного пифагорова дерева после 10 итераций. Отметим, что зрительный эффект остается видимым для нескольких итераций, пока отдельные бруски еще различимы.

