'Невозможные' формы: Экспериментальная графика и теоретические ассоциации
Tamás F. Farkas, Péter Érdi
Аннотация. Конструирование художником Тамашем Фаркашем "невозможных" форм дает импульс к обсуждению научных концепций, связанных с графикой. Обсуждаемые формы представляют собой соединение отдельных элементов логичным образом. Авторы подчеркивают необходимость проведения мыслительных рассуждений для интерпретации "невозможных" форм. В связи с визуализацией движения обсуждаются динамические структуры и разнообразные виды "аттракторов". Самоорганизация, популярная концепция в понимании пространственно-временного развития изменяющихся форм, представлена в качестве последовательной организации линий в виде взаимосвязанной организации отдельных элементов. Также обсуждаются некоторые понятия размерности, связанные с графикой.
I. Персональные мотивации
Данная статья является результатом рассуждений художника Тамаша Фаркаша (Tamás Farkas) (Т.Ф.) и ученого Петера Эрди (Péter Érdi)(П.Э.) на тему принципов организации форм. На обсуждение данного вопроса натолкнули работы Т.Ф., который вот уже более 10 лет исследует принципы организации фигур и реализует свои идеи в виде картин в самых разнообразных техниках.
Основной целью Т.Ф. является создание замкнутых "невозможных" форм, логичным образом соединяя отдельные элементы. Термин "невозможный" отсылает нас к тому факту, что большинство этих структур нельзя реализовать в трех измерениях. Однако, при помощи мыслительных рассуждений они могут быть представлены в пространстве с более чем тремя измерениями.
Необычное представление этих сложных структур венчает очевидный конфликт между плоскостью и квази-пластичными формами на плоскости с одной стороны и объединением разных представлений одной и той же формы с другой.
Мы очень благодарны М.К. Эшеру за логическую ясность и эстетическое наслаждение от его картин. Анализируя работы Эшера, Тормей и Тормей [1] заявляют, что его невозможные картины не являются картинами с двойным смыслом, а визуальным аналогом логических парадоксов. Мы согласны с заявлением D'Amore: "Некоторые картины Эшер делает невозможными лишь для того, чтобы определить собственную организацию и порядок, как, например, с летающими рыбами или структурами пересекающихся форм".
Т.Ф. вдохновлялся не только работами Эшера, но также работами другоих художников, таких как Kaspar Thomas Lenk, Joseph Albers, Frank Stella и Max Bill. Все они исследовали связь между пространством и формой.
Хотя Т.Ф. и родился в той же стране, что и широко известный художник Виктор Вазарели, он попытался найти собственный путь, сознательно отказываясь от зрелищности в своем искусстве.
Работы Т.Ф. вызывают больший интерес в Венгрии скорее среди ученых, нежели среди профессиональных художников. П.Э. полагает, что графика Т.Ф. вызывает эмоциональный эффект у людей, интересующихся изучением структур и процессов, приводящих к формированию таких структур на разных уровнях иерархии. Мы подозреваем, что эксперты в других дисциплинах, таких как кристаллография, структурная химия, теория фазовых переходов и критических явлений, морфогенетика, теория цифровых автоматов, теория динамических систем и синергетика, кроме эстетического значения, могут обнаружить в работах Т.Ф. эвристические аналогии научных концепций.
Мы желаем обсудить общие научные понятия, которые уместны при восприятии данных работ. Отметим, что наши комментарии являются лишь субъективными ассоциациями и не претендуют на теоретические научные толкования.
II. Структуры и аттракторы
Макроскопические структуры часто разделяются на статические и динамические. Разделение осуществляется на основе относительной величины внутренних и внешних взаимодействий.
Статические структуры, будучи инвариантны (по крайней мере, в принципе) с течением времени, сформированы за счет больших усилий между составляющими их элементами. Такие структуры почти невосприимчивы к небольшим внешним воздействиям, но вследствие сильного внешнего воздействия могут быть полностью разрушены.
Динамические структуры формируются за счет постоянного взаимодействия с окружающей средой. Дым и огонь являются наиболее яркими примерами динамических структур в неорганическом мире. В живой природе также можно найти примеры динамических структур. Однако, граница между статическими и динамическими структурами достаточно размыта. Как отметил Haken "... структуры не должны рассматриваться как неизменные, а только развитии ...".
Концепцию динамических структур воплощают два принципа. Во-первых, системы представляют собой сложную иерархию малых и больших структур и шаблонов, в которых отдельные элементы выстраиваются в самоорганизующуюся структуру посредством определенных течений. (Термин "течение" используется в духе Гераклита (540-480 гг. до н.э.)). Во-вторых, течения и структуры могут быть подвергнуты внезапным изменениям, вследствие которых образуются новые самоорганизующиеся структуры, которые будут стабильны некоторое время.
Главная характеристика динамической структуры – ее движение – может быть визуализировано следами или, выражаясь техническим языком, траекториями. В узком смысле, динамические структуры могут рассматриваться как "финальные состояния" неких процессов. Выражаясь техническим языком, квази-постоянные формы могут быть определены как аттракторы некоего вида движения. Грубо говоря, аттрактор – это подмножество фазового пространства динамической структуры, которое "притягивается" к фазовым точкам из других областей фазового пространства в пределах области действия аттрактора.
Точка, а также замкнутая кривая (например, круг или тор) – простейшие аттракторы. В центре внимания теоретических исследований сегодня находится новый класс аттракторов, называемы странными аттракторами. Они активно исследуются в теории хаоса [5,6]. Странные аттракторы имеют особую топологию, напоминающую ленту Мебиуса или бутылку Кляйна, как показано на иллюстрации графика численного решения уравнения Лоренца [7], показывающего движение точки в трехмерного фазовом пространстве (Рис. 1).
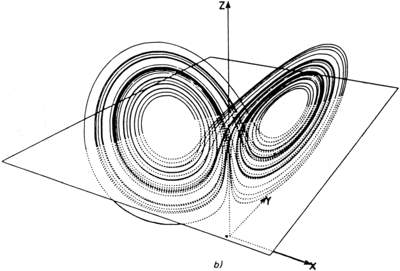
Рис. 1 . Численное решение известной в математической физике уравнения Лоренца,
относящейся к аэродинамическим явленям. Эти "странные аттракторы" имеют особую
топологическую структуру. Их математическая модель может быть использована
для описания явления турбулентности.
Линейные динамические системы имеют тенденцию сходиться к точке равновесия. Замкнутые кривые – более сложный вид аттракторов. Двумерные динамические системы часто сходятся к окружности. В трехмерных системах (и системах больших размерностей) также могут возникать аттракторы. В действительности, принято считать, что "... простые математические модели могут проявлять очень сложную динамику ..." [8].
Вполне вероятно, что динамические системы с размерностью больше, чем три, могут приводить сложному динамическому поведению, формируя аттракторы, даже в случае небольшой нелинейности. Мы полагаем, что замкнутые формы Т.Ф. могут помочь визуализировать аттракторы больших размерностей.
III. Самоорганизация
 Цветная пластина. Девять подсистем, объединенных в одну систему |
Исследования Т.Ф. (термин "исследование" в данном случае представляется оправданным, так как художественное произведение может быть результатом некоторой системных и логических рассуждений) развиваются по двум основным направлениям. Большинство графических работ, представленных в данной статье (рисунки 2 – 7) относятся к первому направлению. Каждая из работ представляет собой замкнутую конструкцию без каких либо «видимых» элементарных составляющих. Они имеют "целостный" характер, так как любая произвольная точка структуры имеет такую же значимость, как и любая другая. Изображение цветной пластины (Color plate) представляет второе направление исследований Т.Ф. – организованное объединение отдельных элементов. Во многих случаях свойства систем, состоящих из множества элементов и подсистем, не являются простым наложений свойств отдельных составляющих. При взаимодействии отдельных подсистем формируются новые свойства системы в целом. Такой вид взаимодействия может приводить к пространственным, временным и пространственно-временным шаблонам в макроскопическом масштабе посредством самоорганизации, как это было предложено в синергетике Хакена.
На рисунке 2 представлена достаточно простая замкнутая организация линий. Однако, их структура значительно сложнее знаменитого треугольника Перноуза.
Непрерывная организация линий на рисунке 3 выступает как невозможный восьмиугольный объект. В центре виден неправильный восьмиугольник. Для интерпретации данной фигуры необходимо понять, что она образована восемью различными видами на одну и ту же фигуру.
Рисунок 4 имеет сложную пространственную структуру, она выглядит одновременно выступающей вперед и уходящей назад за пределы плоскости. Следуя взглядом по линиям, можно обнаружить, что они образуют замкнутый цикл. В дополнение к этому очевидно, что фигура образована видами с четырех разных сторон.
 Рис. 2. Непрерывная форма, организованная по четырем направлениям. Угол изменения направления в вершинах фигуры составляет 90 градусов. Хотя соединения отдельных элементов выглядят реалистичными, в целом форма является "невозможной". |
 Рис. 3. Непрерывная форма, организованная по восьми направлениям. Восьмиконечная звезда образована пересечениями треугольников внутри восьмугольника. При подробном анализе можно увидеть восемь "невозможных" треугольников. |
 Рис. 4. Непрерывная организация, объединяющая четыре разных вида. Сплошная линия в центре фигуры меняет направление под углом 90 градусов. Хотя отдельные элементы трехмерны, структура целиком не может быть воссоздана в реальном мире. |
Тот же принцип организации был использован в рисунке 5. "Звезда Давида" в центре фигуры не была отправной точкой, а явилась результатом процедуры формирования структуры. Форма образована из шести пространственных видов. Свойства фигуры подобны фигуре, представленной на рисунке 4, но степень сложности здесь гораздо выше.
Реалистичная пространственная организация может быть связана и с рисунком 6, а треугольники Пенроуза могут рассматриваться, как логические блоки для организованной формы. Неожиданный визуальный эффект данной фигуры является результатом наложения сразу нескольких явлений. Пространственное скручивание, взаимодействие малых и больших треугольников и самоорганизация трех S-образных форм – вот основные факторы, определяющие характеристики данной формы.
Иерархическая структура формы, представленной на рисунке 7, является более сложной относительно предыдущих форм. Очевидно, линии, образующие призмы, являются промежуточными формами. Эти призмы организованы по шести направлениям. Поворот фигуры на 60 и 120 градусов порождает симметричную фигуру.
 Рис. 5. Замкнутая форма, организованная по шести направлениям. Траектория движения точки по фигуре меняет свое направление в центре, пересекаясь с другим пространственным видом. Это пересечение повторяется шесть раз, прежде чем вернуться в исходную точку. Данная "невозможная" форма образована из шести трехмерных прямоугольников. |
 Рис. 6. Замкнутая организация, начинающаяся из центра, может ассоциироваться с крестом, расположенным вдоль осей координат. Пространственное скручивание, взаимодействие малых и больших треугольников, а также организация S-образных элементов являются фундаментальными элементами это "вращающегося креста". |
 Рис. 7. Эта гораздо более сложная форма образована соединением шести трехмерных форм. Структура организована вокруг шестиугольника в центре. Призмоподобные формы расположены вдоль шести направлений. |
Данная статья - не совсем правильное место, чтобы полностью определить термин "самоорганизация". Однако один из апостолов золотого века кибернетики Росс Эшби утверждал, что поскольку термин "... имеет отношение рассмотрению объектов, как принципиально сбивчивых и неустойчивых, лучше не использовать его ..." [9]. Тем не менее, концепция самоорганизации является очень популярной для описания пространственно-временных изменений материи. [10-12]
Самоорганизующиеся системы могут быть охарактеризованы взаимодействием детерминированных и случайных процессов. Именно это взаимодействие мы соотносим с графическими работами, представленными в данной статье: может быть получено целое семейство фигур при задании начальной конфигурации и алгоритма организации форм. Цветная пластина в начале статьи представляет собой пример совместной организации "цепочек клеток" в различных плоскостях. Другая интересная особенность фигуры – это нарушение симметрии. Обратимся снова к короткой статье Хакена: "Баланс между симметрией и нарушенной симметрией поднимает интересные вопросы не только в естественных науках, но и в эстетике... строгая симметрия может быть скучной..." [13].
IV. Размерности
Четырехмерное пространства рассматривается как мифическое, хотя законы геометрии могут быть расширены на многомерные пространства, вплоть до бесконечности.
Расширение математических знаний не преуменьшает художественную задачу представления многомерных фигур. Трехмерное представление невозможных форм приводит к признанию следующих законов: две плоскости могут иметь общую точку при взгляде на них под определенным углом, хотя в реальности они не будут иметь общей линии. Кроме этого, зрительные парадоксы могут быть получены размещением форм на разных уровнях глубины. Квази-пластичные формы, представленные в двух измерениях, могут быть представлены при помощи мыслительных рассуждений. Теоретически, зрительное восприятие может рассматриваться как проблема обработки данных [14], но в рамках данной статьи мы намерены избежать и объяснений теоретических подходов и проблемы зрительных иллюзий.
Единого определения понятия размерности нет. В знакомом нам Евклидовом пространстве все мы, подчиненные различным аспектам размерности, тем не менее, приходим к одним и тем же выводам. Но, если мы рискнем погрузиться в область неестественного, то различные понятия размерности будут расходиться.[15]
Не вдаваясь в технические детали, мы кратко обсудим фазовые пространства, топологию, фракталы, теорию информации и вложенные размерности [16].
Фазовое пространство, как топологическая размерность, - это целое число, характеризующее количество действительных чисел, которые необходимы для указания конкретной точки в пространстве. Размерности фрактальных множеств [17] могут превышать топологическую размерность. Когда множество (в контексте данной статьи – форма) "простое" (например, окружность или тор), фрактальная размерность представляется целым числом. Множество Кантора считается, наверное, простейшим примером нецелой фрактальной размерности. "Чтобы создать множество Кантора, взяв отрезок прямой, удалите из него центральную треть, затем удалите центральную треть у каждого из оставшихся отрезков и т.д. Фрактальная размерность такого множества равна log 2/log 3" [18]. Грубо говоря, странные аттракторы имеют фрактальную размерность.
Геометрические формы, известные как фракталы, иногда рассматриваются как художественные объекты. "Эстетическая красота стала полной неожиданностью. Наградой." - пишет математик Мандельброт, первооткрыватель фракталов. Один из его бывших коллег Даг Маккена (Doug McKenna) использовал фракталы для создания иллюзорных форм, которые не могут существовать в трех измерениях. Математик Heinz-Otto Peitgen и физик Peter H. Richter [19] создали множестве прекрасных изображений, исследующих топологическую структуру некоторых аттракторов. Перебор некоторых простых карт (используется термин в математическом смысле) при помощи компьютера приводит к фигурам, которые четко показывают дихотомию (противопоставление) простых законов и сложных фигур.
Мы не заявляем, что графические работы Т.Ф. имеют фрактальные размерности, но процедуры построения некоторых из них очень напоминают процедуры, приводящие к фракталам. Конечно, естественным вопросом будет, какое понятие размерности может быть определено для "невозможных' форм.
Благодарности – Мы признательны I. Hargittai и S. Koch за моральную поддержку и комментарии к рукописи.
Перевод статьи
http://members.iif.hu/visontay/ponticulus/rovatok/hidverok/farkas-f-tamas-1-4.html
LEONARDO, Vol. 18 (1985), No. 3, pp. 179-183
© ISAST Pergamon Press Ltd., 1985
© Farkas F. Tamás és Érdi Péter, 1985
