Подкласс невозможных фигур изучаемый теорией узлов
Корин Серф (Corinne Cerf)
Mathematics Dept., CP 216
Université Libre de Bruxelles
B-1050 Bruxelles, Belgium
ccerf@ulb.ac.be
1. Введение
Невозможные фигуры - это пленительные объекты, имеющие отношение к изобразительному искусству, психологии и математике.[1] Лайонел и Роджер Пенроузы (отец и сын) изобрели невозможный треугольник, или трибар (tribar), в 1958 году.[2] (рис. 1) Фигура называется невозможной, когда "восприятие сообщает о противоречии фигуры, но не позволяет разрешить это противоречие, представив непротиворечивую фигуру".[3] Объект, представленный на рис. 1 является невозможной фигурой, так как наш мозг пытается интерпретировать ее как трехмерную (3D) фигуру в евклидовом пространстве с прямыми ребрами и плоскими гранями, вместо, к примеру, двухмерного объекта, нарисованного на бумаге (что я является вполне возможным).
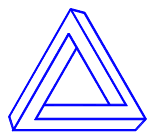
Рис. 1.
Невозможные фигуры вдохновили ученых и исследователей на написание более сотни научных статей (см. библиографию Зенона Кульпы [4]), а также голландского художника М.К. Эшера [5] на создание его знаменитых гравюр.


Рис. 2. (см. [6])
2. Мультибар (Multibar)
Определим мультибар как многогранник [7][8], состоящий из набора брусков прямоугольного сечения, составляющих фигуру правильного многоугольника. Одним из примеров может служить трибар Пенроузов (рис. 1). Но также из брусков могут быть составлены и другие трех-брусочные конструкции на основе правильного треугольника. Некоторые примеры таких конструкций представлены на рис. 3.
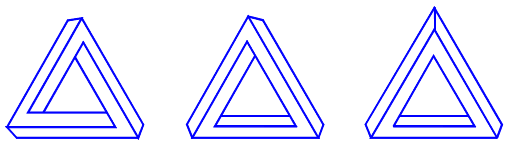
Рис. 3
По интуиции, первые две фигуры выглядят невозможными, а третья - возможной. Рассмотрим теперь семейство фигур, производных от трибара (см. рис. 4).
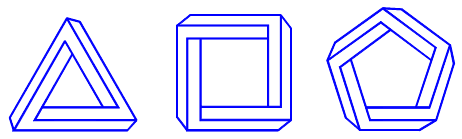
Рис. 4
Изобразим на фигурах с рис. 4 скрытые ребра пунктиром (см. рис. 5).
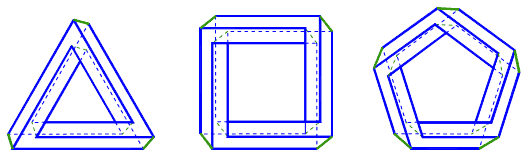
Рис. 5
Сразу можно обратить внимание, что на представленных фигурах имеются ребра двух видов: продольные грани (изображены синим цветом) и поперечные (изображены зеленым цветом). Данная работа была создана под влиянием работ Т.М. Кована (T.M. Cowan) [9][10], который использовал теорию кос (braid theory) для анализа невозможных фигур. Он описывал каждую сторону невозможного многогранника как линию косы. Мы находим более естественным описывать каждое продольное ребро невозможной фигуры как линию косы. Мы намереваемся показать, что теории кос недостаточно для представления мультибара. Необходимо связать косу в узел или соединение надлежащим образом, чтобы мультибар имел только единственное представление.
3. Теория кос (Braid theory)
Рассмотрим основные положения теории кос. n-элементная коса состоит из n линий, направленных сверху вниз. Ни одна из линий не может быть направлена вверх. Линии могут пересекаться друг с другом, и в каждом пересечении та линия, которая расположена позади другой отмечается разрывом. Мы используем обозначения, введенные П. Дехорноем (P. Dehornoy) в работе [11], используя символы в нижнем и верхнем регистре в отличие от использования обозначений si и si-1, для обозначения пересечений (см. рис. 5).
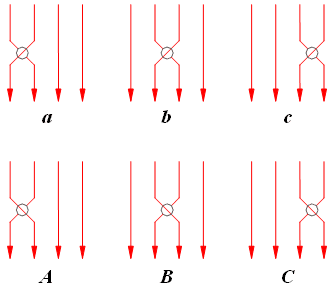
Рис. 6
Пересечения в косах формируются в группы посредством операции соединения при помощи следующих соотношений.
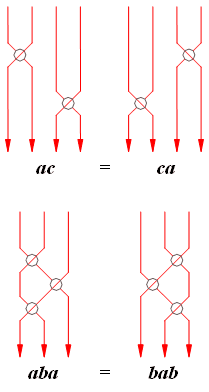
Рис. 7
Первое соотношение (ac = ca) верно для любых двух символов расположенных друг от друга на расстоянии не менее 2 символов внутри алфавита. Второе соотношение (aba = bab) верно для любых двух последовательных символов алфавита. Также необходимо ввести правило инверсии для любой группы, то есть aA = bB = cC = тривиальность. Тривиальность n-элементной косы означает, что она соответствует косе из n непересекающихся линий.
Рассмотрим теперь один из углов многогранника с рис. 5. Соответствующая этому углу коса представлена на рис. 8.
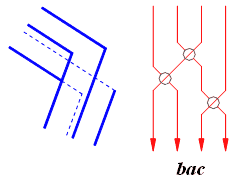
Рис. 8.
Четырехэлементные косы, соответствующие трибару, невозможному квадрату и невозможному пентагону имеют следующий вид соответственно bacbacbac, bacbacbacbac, и bacbacbacbacbac.
Следует обратить внимание, что многогранники представленные на рис. 4 могут быть изображены и в виде, представленном на рис. 9.
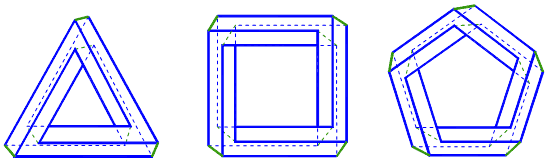
Рис. 9.
Тогда один угол каждого из таких многогранников будет представлен следующей косой (см. рис. 10).
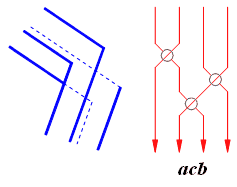
Рис. 10.
Четырехэлементные косы, соответствующие трибару, невозможному квадрату и невозможному пентагону, представленным на рис. 9, будут иметь следующий вид соответственно acbacbacb, acbacbacbacb, и acbacbacbacbacb.
4. Узлы и соединения
Мы подошли вплотную к понятию замкнутой косы, представленной на рис. 11. Замыкание косы преобразует ее в узел (или соединение), который является представлением замкнутой линии (или нескольких линий) в трехмерном пространстве.
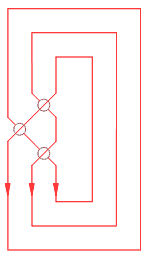
Рис. 11.
Теорема Маркова [12] гласит, что различные косы после замыкания соответствуют одному и тому же узлу, если они преобразуются к нему посредством конечного числа изменений двух видов:
- Объединение (в случае рассмотрения цепочек пересечений мультибаров мы перемещаем пересечение b с одного конца косы в другой по линии соединения);
- Изменение, при котором к косе добавляется линия, образуя пересечение между двумя крайними линиями. (Данное изменение не входит в контекст решаемой задачи, так как косы мультибаров ограничены четырьмя линиями)
Таким образом, видно, что для мультибаров, представленных на рис. 4 существует только одно представление узла, независимо от угла обзора фигуры.
Преимущество использования узлов перед использованием кос при анализе невозможных фигур более ярко видно, если мы будем рассматривать "магическую пентаграмму" (рис. 12 слева), представленную в работе Л. Саллоуса (Sallows)[13] и на последней странице книги Ф.Дж.Светца (F.J. Swetz)[14]. Представленный вариант пентаграммы в виде брусков удовлетворяет нашему определению мультибара.

Рис. 12.
Четырехэлементная коса, соответствующая пентаграмме, bacbacbacbacbac (или acbacbacbacbacb в зависимости от угла обзора) неотличима от косы невозможного пентагона с рис. 4. В противоположность узлу, соединение, соответствующее невозможной пентаграмме, значительно отличается от соединения, соответствующего невозможному пентагону, так как в этом случае принимается во внимание расположение брусков в пространстве друг относительно друга. В этом случае, необходимо рассматривать сопровождающее соединение, дружественный узел которого изображен на рис. 12 справа. Это дружественное соединение может быть нетривиальным, так как дружественный узел является нетривиальным.
Если изобразить (см. рис. 13) скрытые ребра треугольника (см. рис. 3), который является возможной фигурой, легко увидеть, что соответствующее ему соединение является тривиальным четырехэлементным соединением.
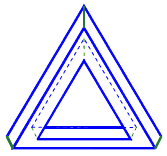
Рис. 13.
В заключение, мы подошли к формулировке критерия, в соответствии с которым, можно определить, является ли мультибар невозможной фигурой: "Если узел или соединение, соответствующее мультибару, отличается от тривиального четырехэлементного соединения, тогда мультибар является невозможной фигурой.
Благодарности
Большое спасибо Френсису Бейкенхауту (Francis Buekenhout), который открыл мне "невозможную пентаграмму" и побудил написать данный текст.
Литература
- B. Ernst. Adventures with Impossible Figures. Tarquin, Norfolk, 1986.
- L. S. Penrose and R. Penrose (1958). Impossible objects: A special type of illusion. British J. of Psychology 49, 31-33.
- S. W. Draper (1978). The Penrose triangle and a family of related figures. Perception 7, 283-296.
- Z. Kulpa (1983). Are impossible figures possible? Signal Processing 5, 201-220.
- M. C. Escher. The Graphic Work of M. C. Escher. Ballantine Books, New York, 1971.
- The reproductions of Escher's drawings come from the following internet
pages:
top: www.ex-cult.org/fwbo/fwbosection2.htm;
bottom: www.mgdesign.org/routeur_uk.php3?page=modelisation_uk.php3 - H. S. M. Coxeter. Regular Polytopes. Dover, New York, 1973.
- F. Buekenhout. Une Définition de Polyédre. Centre de Documentation Pédagogique, Université Libre de Bruxelles, Bruxelles, 2002.
- T. M. Cowan (1974). The theory of braids and the analysis of impossible figures. J. Math. Psychology 11, 190-212.
- T. M. Cowan (1982). Turning a penrose triangle inside out. J. Math. Psychology 26, 252-262.
- P. Dehornoy (1997). L'art de tresser. Dossier Pour la Science, La Science des Noeuds (avril 1997), 68-74.
- A. A. Markov (1936). Ueber die freie aquivalenz der geschlossenen Zopfe. Recueil de la Soc. Math. de Moscou 43, 73-78.
- L. Sallows (1995). The impossible problem. The Mathematical Intelligencer, Vol 13, No 2, 1991, p.33.
- F. J. Swetz (Ed.). From Five Fingers to Infinity; A Journey through the History of Mathematics. Open Court, Chicago, 1994.
- C. C. Adams. The Knot Book. Freeman, New York, 2001.
Перевод статьи Corinne Cerf "A family
of impossible figures studieb by knot theory"
http://www.mi.sanu.ac.yu/vismath/cerf/
© Перевод Влада Алексеева
