Применение теоремы Эйлера к мультибарам
Автор - Кристина Юсупова (uko2304@mail.ru)
Статья из научно-исследовательской работы "Мультибары, их свойства и приложение", 2013 г.
Научно-практическая конференция "Шаг в будущее", г. Наро-Фоминск,
Шестнадцатая научная конференция молодых исследователей "Шаг в будущее.Москва", МГТУ им. Н.Э. Баумана
Объектами данного исследования являются невозможные фигуры, то есть плоские рисунки, которые создают впечатление трехмерных объектов таким образом, что объекты, предложенные нашим пространственным восприятием, не могут существовать, так что попытка создать их ведет к геометрическим противоречиям, ясно видимым наблюдателем. Существует великое множество различных невозможных фигур, но для своего исследования я выбрала определенный вид данных объектов – это мультибары. Мультибары – это фигуры, состоящие из определенного количества брусков квадратного сечения, соединенных друг с другом концами в невозможный многоугольник (под понятием "многоугольник" в данном случае принято считать невозможную фигуру, состоящую из n-брусков, последовательно соединенных друг с другом и образующих замкнутую фигуру).

Рис. 1
Различают скругленные и нескругленные мультибары. Скругленными называют невозможные объекты, которые состоят из скругленных углов двух возможных форм (рис. 1), а нескругленные мультибары – это объекты, у которых четко выражены вершины (например, трибар относится к этому типу муьтибаров), и именно их свойства были исследованы в данной работе (рис. 2).
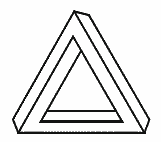
Рис. 2
Теорема Эйлера для многогранников впервые была опубликована в журнале Петербургской Академии наук в 1752 г. в работах великого математика Леонарда Эйлера "Элементы учения о телах" и "Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями". Эта теорема устанавливает связь между числом вершин, ребер и граней для выпуклого многогранника. Теорема имеет следующую формулировку: "Пусть В – число вершин выпуклого многогранника, Р – число его ребер и Г – число граней. Тогда верно равенство:
В – Р + Г = Х
Число Х называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2.
Попробуем выяснить, можно ли применить теорему Эйлера для многогранников к мультибарам. Один из известнейших современных художников-микроминиатюристов Анатолий Коненко, делая соответствующие расчеты, выявил, что для моделей Амес равенство в формуле Эйлера сохраняется, а в мультибарах равенства в формуле не было (модель Амес – это трехмерный объект, одной из проекций которого является мультибар).
Проведя дополнительное исследование по применению теоремы Эйлера к невозможным фигурам, мне удалось выявить очень интересный факт. Для начала обратим внимание на то, что в формулировке теоремы фигурируют такие понятия как "вершина", "ребро" и "грань", и для того, чтобы выполнять соответствующие расчеты, необходимо дать четкое определение этим понятиям для дальнейшей работы с ними (определения "вершин", "граней" и "ребер" для мультибаров).
Вершиной, или крайней точкой мультибара, называется любая его точка, которая не является внутренней точкой никакого отрезка, целиком принадлежащего этому мультибару.
Ребро - это отрезок, хотя бы один конец которого является вершиной мультибара. Но следует отметить, что обязательно одно ребро должно принадлежать двум граням.
Гранью мультибара является часть его поверхности, ограниченная ребрами этого объекта.
Учитывая данные определения, я вычислила число вершин, граней и ребер у ряда невозможных фигур и вывела новую формулу, прототипом которой стала формула Эйлера для многогранников. С помощью этой формулы мы получим характеристику, которая наблюдается только в замкнутых однокомпонентных мультибарах. Эта характеристика показывает связь между числом вершин, ребер и граней невозможных фигур.
Она имеет следующий вид:
Х = Р / ( В + Г )
Исходя из выведенной формулы, в таблице 1 представлены первые 4 представителя нужных нам мультибаров, соотношения вершин, ребер и граней которых дают нам число Х = 3/2.
| Мультибары | Число вершин (В) | Число ребер (Р) | Число граней (Г) | |
|---|---|---|---|---|
 |
6 | 18 | 6 | 3/2 |
 |
8 | 24 | 8 | 3/2 |
 |
10 | 30 | 10 | 3/2 |
 |
13 | 36 | 12 | 3/2 |
Заметим, что в таблице, исходя из расчетов, мы получаем числа вершин и граней
равные между собой (т.к. в местах соединения брусков объекта мы получаем 2 вершины,
а из-за их "невозможного" соединения с двух сторон объекта,
видимой и невидимой, образуется по
Р = 4 · n + 2 · n,
где n – число составляющих объект брусков
Согласно расчетам, число Х в этой формуле для невозможных фигур будет равно 3/2, что как раз видно в таблице 1, и это можно доказать.
Доказательство: индукция по k.
База, В = Г = k
Рассчитаем X для В = Г = ( k + n ), где n – четное число
Переход: предположим, что
тогда
откуда
У всех нескругленных однокомпонентных невозможных фигур число вершин равно числу граней, а число ребер в 3 раза больше числа одного из этих параметров, что при расчете по видоизмененной формуле Эйлера, применяемой для мультибаров, дает характеристику Х = 3/2.
Следует отметить, что к скругленным мультибарам данную формулу мы не применяем.
Для создания невозможных фигур из таблицы 1 было использовано приложение Impossible Puzzle.
Решение некоторых задач с помощью новой формулы для мультибаров
Задача №1. Найдите число вершин для 125-угольного мультибара.
Решение:
Известно число углов мультибара: n = 125.
Известно, что число ребер рассчитывается по формуле
Подставив в формулу значение n, мы получаем:
Для того, чтобы найти число вершин мультибара, необходимо воспользоваться
основной формулой соотношения элементов невозможных объектов:
Так как В = Г = y, то: 900 / 2y = 3/2; 6y = 1800; y=300
Ответ: В=300
Задача №2. Существует ли такой невозможный объект, у которого число вершин равно 960, а число ребер – 4800?
Решение:
Запишем основную формулу, выражающую соотношение между числом вершин, граней и ребер мультибаров:
Известно, что Р = 4800, В = 960
Так как В = Р: Х' = 4800 / ( 960 + 960 ) = 4800 / 1920 = 5/2
Ответ: Мультибара с данным числом вершин и ребер не существует.
Задача №3. Известно, что мультибар имеет 46 граней. Чему будет равно число его углов?
Решение:
Известно, что число ребер рассчитывается по формуле:
где n – число углов у мультибара.
Подставим это выражение в основную формулу:
Ответ: Число углов равно 23.
