Геометрическое представление чисел
Графическое представление геометрического способа умножения чисел, в записи которых присутствует 0
Автор - Кристина Юсупова (uko2304@mail.ru)
Статья из научно-исследовательской работы "Изучение мира оптических иллюзий с точки зрения математики.
Достижения в исследовании невозможных фигур",
конференция "Наше Подмосковье", номинация "Научный прорыв", 2013 г.
Не так давно при раскопках здания административных служб в городе Нара, древней столице Японии (VIII век), археологами была найдена деревянная табличка с фрагментом таблицы умножения (рис. 1) . Самое интересное, что, судя по всему, ею пользовались вовсе не дети, а взрослые. Эта таблица умножения несколько отличается от той таблицы, которую проходят школьники школ нашей страны. Умножение чисел по-японски выглядит иначе: оно имеет графическое представление, что, как выяснилось, намного удобнее и легче осваивается школьниками и взрослыми людьми.

Рис. 1
Данный способ позволяет без труда умножать как однозначные числа, так и двузначные, трехзначные и т.д. Разберем подробно геометрический способ умножения чисел. Итак, весь смысл такого умножения заключается в том, что каждую цифру в записи множителей мы представляем графически, т.е. прямыми линиями, количество которых соответствует определенной цифре. Отметим, что линии одного множителя должны пересекать линии другого множителя, а сумма пересечений и есть их произведение.
Рассмотрим геометрический способ на примере. Умножим число 32 на 21 (рис. 2). На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера. Сначала 32: 3 красные линии и чуть ниже - 2 синие. Затем 21: перпендикулярно уже нарисованным, рисуем сначала 2 зеленые, затем – 1 розовую. ВАЖНО: линии первого числа рисуются в направлении из верхнего левого угла в нижний правый, второго числа - из нижнего левого в верхний правый. Затем считаем количество точек пересечения в каждой из трех областей (на рисунке области обозначены в виде окружностей). Итак, в первой области (область сотен) - 6 точек, во второй (область десятков) - 7 точек, в третьей (область единиц) - 2 точки. Следовательно, ответ: 672.
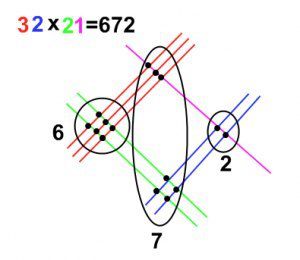
Рис. 2
В разных источниках информации, где упоминается об умножении чисел геометрическим способом, я не встречала ни одного примера, где в записи хотя бы одного из множителей присутствует 0, или объяснение того, как умножать такие числа. Тогда мне пришла идея, как можно графически показать произведение с 0 в записи одного из множителей.
Для начала ознакомимся с принципом умножения чисел в исследуемой ситуации: при умножении двух чисел, в записи которых присутствует 0, геометрическим способом умножения подсчет пересечений линий всех цифр, входящих в запись множителей, с нулем дают 0 пересечений. Справедливость этого правила умножения японским способом с нулем доказана, теперь осталось только проиллюстрировать данное правило. В подобных примерах умножения с нулем я решила задействовать мультибары как объекты представления произведения чисел. Как мы знаем из определения, мультибары – это невозможные фигуры, конструкцию которых составляют бруски квадратного сечения. Как раз такие бруски я предлагаю использовать при нахождении произведения чисел вместо линий, которые были взяты в выше упомянутом примере. Итак, рассмотрим на примере: умножим 102 на 22. Для начала изобразим число 22 графически (рис. 3). Мы видим, что горизонтальные бруски соответствуют цифрам, из которых состоит число: 2 и 2.

Рис. 3
Теперь разберем число 102 (рис. 4). В его записи присутствует 0. Его я изобразила как один заштрихованный брусок, выделила его цветом, чтобы помнить, что все пересечения с ним не играют роли в результате.
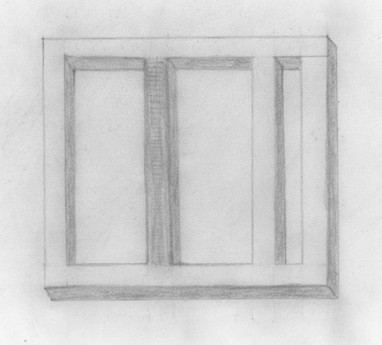
Рис. 4
Теперь попробуем графически изобразить данное произведение (рис. 5). Здесь мы получаем невозможное пересечение бруска, соответствующего 0 в записи числа 102, с брусками числа 22. Из этого рисунка мы видим, что ответом в данном примере будет число 2244.

Рис. 5
Такое графическое представление произведений с содержанием 0 в записи одного из множителей несет 2 пользы: первое, это то, что мы наглядно видим несуществование пересечений с нулевым бруском, соответственно считаем все оставшиеся пересечения и получаем ответ; второе, это то, что геометрический способ умножения чисел, в записи которых есть 0, помогает нам получить огромное количество новых мультибаров, что пополнит коллекцию невозможных фигур (например, рис. 6).

Рис. 6
