Многомерная геометрия
Глава 1 - Азы многомерной геометрии
"Бог действует по геометрическим линиям."
Платон
Вообще сама идея четвертого измерения не раз привлекала к себе внимание крайних мистиков. Любопытно, что происхождение этой идеи связано с Платоном (427-347 гг. до н.э.), самым крупным древнегреческим философом-идеалистом. Впервые же слова "n-мерное пространство" прозвучали в 1854 году в речи Бернгадра Римана (1826-66) при вступлении его на должность преподавателя Геттингенского университета.
В современном учебнике по геометрии написано: "Многомерная геометрия – один из самых сложных разделов науки". И до сих пор решение этой темы не давалось профессиональным математикам, хотя еще в 1910 году был проведен конкурс на лучшую работу о четвёртом измерении, в котором приняли участие 245 математиков из разных стран мира.
Тогда профессиональным математикам удалось теоретически рассчитать количество единичных элементов (вершин, ребер, граней и кубов) в четырехмерном гиперкубе, даже определить некоторые принципы расположения этих "единичных элементов" гиперкуба. Но две их ошибочные геометрические версии трёхмерной проекции четырёхмерного гиперкуба до сих пор используются в работах на эту тему.
Спустя ровно 100 лет (!), - в 2010 году - я определила "Универсальный метод построения (черчения) трёхмерных проекций гиперкубов любых n- мерных измерений в любых проекциях и ракурсах". Вот действительно, - мистика какая-то ...
В n-мерной геометрии, где n = 0, 1, 2, 3, 4, 5, 6, 7,..., геометрическим символом каждого измерения служат так называемые единичные геометрические фигуры. Так, геометрическим символом 0-мерного измерения является точка, 1-мерного измерения – отрезок прямой, 2-мерного измерения – квадрат, 3-мерного измерения – куб. Геометрический символ 4-мерного измерения получил удачное название "гиперкуб" [гипер- (от греч. hyper – над, сверх), часть сложных слов, обозначающая превышение нормы].
А еще геометрический символ 4-мерного измерения получил название тессеракт, геометрический символ 5-мерного измерения - пентеракт, шестимерного измерения – хексеракт, и т.д.
Занимаясь этой темой с 2004 года и создавая из трубочек и лески модели трехмерных проекций геометрических символов 4-мерного и 5-мерного измерений, я назвала их соответственно: трехмерная проекция четырехмерного гиперкуба (3ПГК-4) и трехмерная проекция пятимерного гиперкуба (3ПГК-5), то есть гиперкуб любого n-мерного измерения удобно называть "гиперкуб-n" (ГК-n), - сразу понятно о гиперкубе какого измерения идет речь. Зачем усложнять геометрию, придумывая для гиперкубов пятого, шестого и т.д. измерений новые специальные названия?
Да, конечно, представить себе именно гиперкуб-4, гиперкуб-5 и т.д. в их родном n-мерном пространстве трудно, но осмыслить и определить трехмерные проекции гиперкубов высших измерений и их геометрические особенности – дело вполне реальное. Из трубочек и лески мною уже созданы модели трехмерных проекций гиперкубов 4-го, 5-го и 6-го измерений. В случае надобности можно создавать модели трехмерных проекций гиперкубов и более высоких измерений.
Осмысливать геометрические особенности проекций гиперкубов-n намного легче не по чертежам, а по моделям их трехмерных проекций.
В работе [4] выведены алгебраические формулы для определения количества единичных геометрических элементов, составляющих n-мерные гиперкубы и их проекции (вершин, ребер, граней, кубов). Эти данные приведены в таблице 1.1.
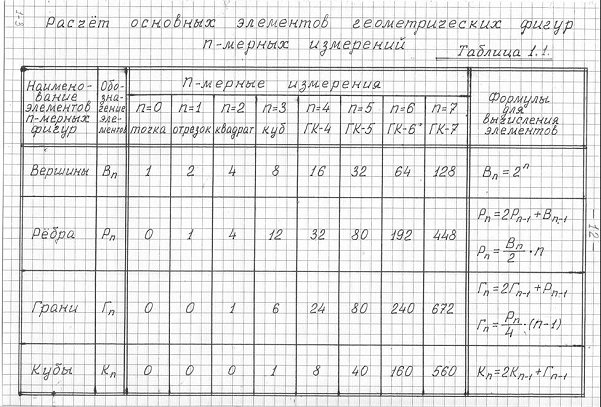
Таблица 1.1
А вот теперь, для начала предлагаю вам чертеж (рис.1.1), где на одной странице представлены во фронтальной проекции геометрические символы семи измерений. Это наиболее простой и достаточно удобный способ черчения трехмерных проекций n-мерных гиперкубов.
Более того, эта фронтальная проекция важна тем, что именно эта проекция очень наглядно подскажет любому профессиональному геометру, как начертить трехмерные проекции гиперкубов и следующих измерений: седьмого (3ПГК-7), восьмого (3ПГК-8), девятого (3ПГК-9) и т.д.
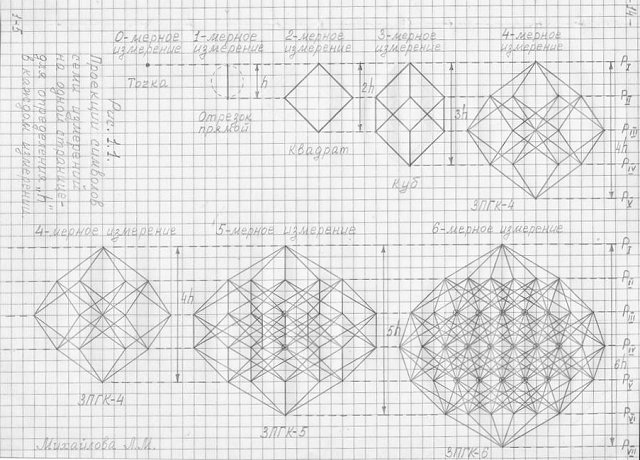
Рис. 1.1
Давайте осмысливать рис. 1.1.
Смотрите, в какое "интересное", "особое" положение поставлены куб, квадрат и отрезок прямой. Евклидова геометрия определила этим геометрическим фигурам более "устойчивое" положение. Многомерная же геометрия требует рассматривать положение этих геометрических символов измерений именно в такой позиции – для определения "h" в проекциях геометрических символов каждого (абсолютно любого) измерения.
Именно эта фронтальная проекция дает возможность схематично провести через вершины проекций всех n-мерных геометрических символов параллельные плоскости (Р), которые на рис. 1.1 изображены в виде пунктирных линий (прямых). Каждая пунктирная прямая (плоскость Р) пронумерована римскими цифрами.
На рис. 1.1. семь таких плоскостей: PI, PII, PIII, PIV, PV, PVI и PVII, причем, что очень важно, эти параллельные между плоскости отстоят друг от друга на равную величину "h".
Величину "h" назовем "ярусом". Количество этих "ярусов" в n-мерном геометрическом символе соответствует числовому значению именно этой мерности, т.е. числу n.
В трехмерный проекциях всех n-мерных гиперкубов ни одна вершина не может находиться вне этих плоскостей.
Для осмысления трехмерных проекций гиперкубов-n эти плоскости очень важны – эти плоскости делят фигуры символов всех n-мерных измерений на хорошо известные геометрические фигуры: пирамиды, прямоугольные призмы, скошенные призмы, параллелепипеды и др.
А это значит, что через вершины трехмерных проекций гиперкубо-n можно вписать разные хорошо известные геометрические фигуры, и с их помощью определить (рассчивать) все геометрические параметры трехмерных проекции гиперкубов-n.
Для пояснения вышесказанного сначала рассмотрим эту особенность плоскостей на примере трехмерного куба.
Поставим куб в "интересное" положение, но для наглядности слегка изменим ракурс. (рис. 1.2).
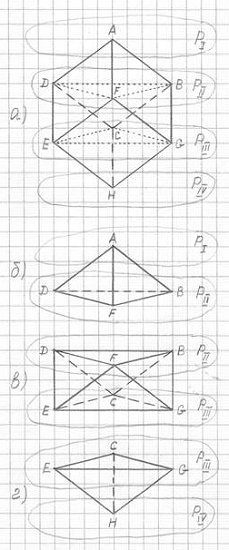
Рис. 1.2
а) Куб ABCDEFGH, через вершины которого проведены параллельные плоскости PI, PII, PIII, PIV;
б) Верхняя треугольная пирамида ABFD, где ребра основания BFD равны диагонали грани куба;
в) Скошенная треугольная призма. Ее основания ΔBFD и ΔCEG, а ее 6 боковых граней-треугольников образованы шестью ребрами куба;
г) Нижняя треугольная пирамида HCEG, геометрически равная верхней пирамиде ABFD.
В рис. 1.2 куб "поставлен" на одну из его больших диагоналей – AH. Но куб имеет четыре больших диагонали: AH, BE, CF и DG, и если мы вместо диагонали AH используем любую из оставшихся диагоналей, это не изменит геометрического смысла рис. 1.2. С таким же успехом мы можем поменять вершины A и H. Это может говорить о том, что в рис. 1.2 в первой плоскости (PI) может оказаться любая из восьми вершин куба ABCDEFGH, что не изменит геометрического (но не физического!) смысла рис. 1.2.
Итак, в первой плоскости (PI) может оказаться любая из восьми вершин куба.
В трехмерной проекции четырехмерного гиперкуба (3ПГК-4) таких вершин шесть. А вот в трехмерной проекции пятимерного гиперкуба (3ПГК-5) и во всех (!) последующих 3ПГК-6, 3ПГК-7,..., 3ПГК-n таких вершин только две. Об этом будет рассказано позже.
Продолжим осмысливать рис 1.1. Вы видите в чертеже фронтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5) две вершины, обведенные кружочками. В этих двух вершинах сходятся по девять ребер, во всех остальных вершинах – по пять. Что это такое?
Это – визуальное совмещение вершин, а так как эти совмещенные на чертеже вершины соединены между собой и ребром, то это значит, что в данном чертеже 3ПГК-5 визуально совмещенными оказались не только две пары вершин, но и два ребра. Следовательно, если вы подсчитаете количество вершин на этом чертеже 3ПГК-5, то их окажется 30, а не 32, и количество ребер на чертеже 79, а не 80.
А вот чертеж той же трехмерной проекции пятимерного гиперкуба (3ПГК-5), и тоже во фронтальной проекции, но только со слегка смещенным ракурсом (рис. 1.3).
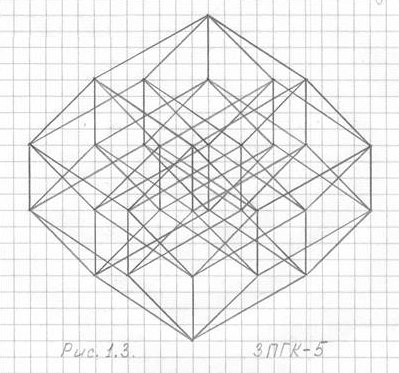
Рис. 1.3
На этом чертеже нет ни одного совмещения вершин, то есть данный чертеж 3ПГК-5 содержит все 32 вершины и 80 ребер.
Давайте рассмотрим ситуацию совмещения вершин и ребер на примере трехмерного куба ABCDEFGH (рис. 1.4).
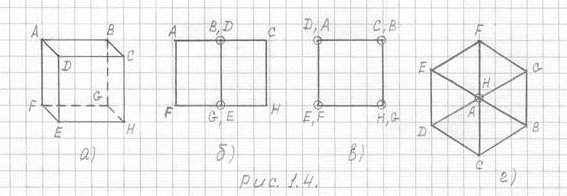
Рис. 1.4
На рис.1.4 куб ABCDEFGH представлен в четырех проекциях: а), б), в), г). Комментировать рис. 1.4 излишне, - геометру легко понять, почему некоторые вершины обведены кружочками, и что из этого следует.
Итак, в зависимости от выбранного ракурса изображения в чертежах трехмерных проекций гиперкубов-n могут совместиться и вершины, и ребра, и грани, и кубы (например, 3ПГК-6 на рис. 1.1). Все это происходит не хаотично, а потому, что все эти геометрические фигуры (3ПГК-n) идеально правильны по своей сути.
Прошу учесть также, что начертить "по клеткам", как это сделано здесь, абсолютно точно, без искажений возможно лишь трехмерную проекцию четырехмерного гиперкуба (3ПГК-4). Начертить "по клеткам" трехмерные проекции гиперкубов более высоких измерений (3ПГК-5, 3ПГК-6, 3ПГК-7 и т.д.) возможно лишь с большей или меньшей погрешностью по той простой причине, что на листе бумаги "в клетку" через вершины клеток невозможно начертить правильные пятиугольник, шестиугольник, семиугольник и т.д. Компьютерная графика была бы здесь более уместна.
