Невозможный мир

Многомерная геометрия

Глава 2 - Трехмерная проекция четырехмерного гиперкуба (3ПГК-4)

В работе "Постигая четырехмерное измерение, мы приходим к геометрии n-мерных пространств" [3] определен метод построения (черчения) трехмерной проекции четырехмерного гиперкуба (3ПГК-4) с помощью трехмерной проекции осей координат для четырехмерного измерения.

Метод определения трехмерной проекции осей координат для четырехмерного измерения

Идея принять большие диагонали куба за трехмерную проекцию осей координат для четырехмерного измерения возникла у автора в голове почти моментально. Для проверки этой идеи исследуем куб (рисунки 2.1 и 2.2), посмотрим, что он выдаст.

Ни рис. 2.1 изображен куб ABCDEFGH, примем длину ребра куба равной величине a. Через геометрический центр О куба и геометрические центры (1, 2, 3, 4, 5, 6 ) каждой из шести граней куба проведем оси +X–X , +Y-Y и +Z-Z, то есть получим Декартову систему координат, которой пользуются более 350 лет. Проведем четыре большие диагонали куба.

Исследуем все вершины куба на предмет их знакового значения (+ или -) относительно Декартовой системы координат. Результаты этого исследования сведены в таблицу 2.1.


Таблица 2.1

Проведем анализ знаковых значений вершин куба.

Сразу видно, что только две вершины D и F, являющиеся крайними точками большой диагонали куба FD, имеют все три одинаковых знака: вершина F (+X, +Y, +Z) и вершина D (-X, -Y, -Z).

А из этого следует, что куб сам указал на четвертую ось в новой для нас трехмерной проекции системы осей координат для четырехмерного измерения, причем указал и ее знаковое направление.

Обозначим эту ось буквой T - от греческого слова "tetra", означающего "четыре".

Итак, в новой для нас трехмерной проекции системы осей координат для четырехмерного измерения определена главная ось, проходящая через вершины куба F и D, причем направление оси от центра О в сторону вершины F является положительным направлением (+T), а направление оси от центра О в сторону вершины D является отрицательным направлением (-T).

Для того, чтобы определить, как в каком направлении расположатся три остальные оси в трехмерной проекции системы осей координат для четырехмерного измерения Xг, Yг и Zг (индекс "г" - от слова гиперкуб), проведем знаковый анализ остальных шести вершин A, B, C, E, G и H куба, пользуясь таблицей 2.1 и рисунком 2.2.


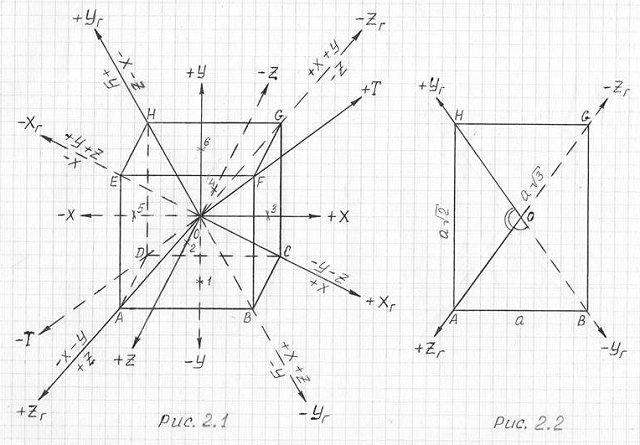
Рис. 2.1, Рис. 2.2

1. Положительные значения координаты X (+X) из оставшихся шести вершин A, B, C, E, G и H куба содержат вершины B, C и G, значит, это и является областью положительного икса, и ось +Xг проходит через среднюю между B, C и G вершину куба C.

Отрицательные значения координаты X (-X) из оставшихся шести вершин куба содержат вершины A, E и H, значит, это и является областью отрицательного икса, и ось –Xг проходит через среднюю между A, E и H вершину куба E.

2. Положительные значения координаты Y (+Y) из оставшихся шести вершин куба содержат вершины E, H и G, значит, это и является областью положительного игрека, и ось +Yг проходит через среднюю между E, H и G вершину H.

Отрицательные значения координаты Y (-Y) из оставшихся шести вершин куба содержат вершины A, B и C, значит, это и является областью отрицательного игрека, и ось –Yг проходит через среднюю между A, B и C вершину B.

3. Положительные значения координаты Z (+Z) из оставшихся шести вершин куба содержат вершины E, A и B, значит, это и является областью положительного зет, и ось +Zг проходит через среднюю между E, A и B вершину A.

Отрицательное значение зет (-Z) из оставшихся шести вершин куба содержат вершины C, G и H, значит, это и является областью отрицательного зет, и ось –Zг проходит через среднюю между C, G и H вершину G.

Итак, определены все четыре оси трехмерной проекции системы осей координат для четырехмерного измерения: ось +T-T проходит через вершины куба F и D соответственно, ось +Xг-Xг проходит через вершины C и E, ось +Yг-Yг проходит через вершины H и B, ось +Zг-Zг проходит через вершины A и G.

Это великолепный подарок куба!

Теперь, чтобы определить углы между осями трехмерной проекции системы осей координат для четырехмерного измерения, обратимся к рисунку 2.2, где изображена плоскость ABGH, которая является плоскостью симметрии куба, в этой плоскости лежат две оси +Zг-Zг и +Yг-Yг трехмерной проекции системы осей координат для четырехмерного измерения.

1. Из треугольника AОB определим угол AОB по теореме косинусов:

AB2 = AO2 + OB2 - 2 · AO · OB · cos ∠AOB (2.1)

При принятой величине AB = a согласно теореме Пифагора AH = BC = a2 и AG = BH = a3; AO = OB = a3/2.

Подставив в уравнение (2.1) значения AB, AО и ОB, получим:

cos ∠AOB = 1 3 = 0,3333... ∠AOB = 70°32' (2.2)

2. Определим угол AОH, то есть угол, заключенный между осями +ZгО+Yг или –YгО-Zг:

∠AOH = ∠BOG = ... = ∠BOE = 180° - 70°32' = 109°28' (2.3)

Таким образом, определены и углы между осями трехмерной проекции системы осей координат для четырехмерного измерения.

Замечательно то, что центр О является общей точкой для обеих систем координат, что очень удобно при переходе из одной системы координат в другую.

Четырехмерное пространство имеет свои особенности и законы. В четырехмерном пространстве меняются размерности всех единиц измерения, которыми мы пользуемся в нашем трехмерном мире. Но пользуясь логикой и рассуждениями по аналогии можно проследить, выявить и вычислить эти изменения в размерностях.

Наш трехмерный куб, такой всем близкий и знакомый, дарит нам еще одну свою тайну – единицу длины ребра в четырехмерном пространстве. Посмотрите на рис. 2.1: точками 1, 2, 3, 4, 5 и 6 обозначены геометрические центры каждой грани куба. Через эти точки проходят оси Декартовой системы координат, и при принятой величине длины ребра куба, равной a, расстояние от центра О до всех точек 1, 2, 3, 4, 5 и 6 равно a/2.

Большие диагонали куба AG, BH, CE и DF, являющиеся образующими оси трехмерной проекции системы координат для четырехмерного измерения, равны a3 и, соответственно, половина длины этих диагоналей, то есть расстояние от центра О до всех точек (вершин куба) A, B, C, D, E, F, G и H, равно a3/2.

Мне кажется, что теперь не трудно догадаться, что отрезок OB, например, расположенный на оси OX в декартовой системе координат и равный величине a/2, перемещаясь из трехмерного пространства в четырехмерное, превратится в отрезок OC, расположенный на оси O+Xг (или в отрезок OE, расположенный на оси O+Xг), и теперь его длина определится величиной a3/2.

Это говорит о том, что наш трехмерный куб с длиной ребра a, перемещаясь в четырехмерное пространство, превратится в четырехмерный гиперкуб с длиной ребра aг, при этом:

a Г = a 3 ≈ 1,732 · a (2.4)

Метод построения трехмерной проекции четырехмерного гиперкуба (3ПГК-4) на чертеже

Итак, создав из трубочек и лески модель трёхмерной проекции четырехмерного гиперкуба (3ПГК-4) (см. фотографию 1), приступим к построению 3ПГК-4 на чертеже, то есть перенесем 3ПГК-4 во второе измерение – на плоскость листа бумаги (см. рис. 2.3).


Фото 1

Фото 2

На чертеже строим куб ABCDEFGH, приняв длину ребра равной величине a, и через вершины куба проводим оси +T-T, +Xг-Xг, +Yг-Yг, +Zг-Zг новой системы координат для четырехмерного измерения.


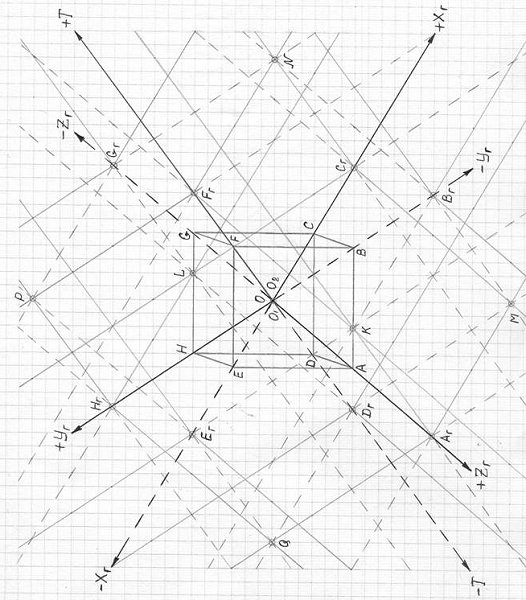
Рис. 2.3

Так как на созданной модели 3ПГК-4 видно, что восемь внутренних ребер модели сходятся в центре 3ПГК-4, причем своим взаимным положением относительно друг друга эти восемь внутренних ребер полностью соответствуют всем осям проекции системы координат для четырехмерного измерения, то, следовательно, на продолжении новых осей координат и расположатся восемь вершин (Aг, Bг, Cг, Dг, Eг, Fг, Gг, Hг) трехмерной проекции четырехмерного гиперкуба.

Расстояние от центра O до этих вершин равно длине ребра 3ПГК-4 aг, при этом aГ=a3 ≈a·1,732, то есть удвоенному расстоянию от центра O до лежашей на этой оси вершины проекции исходного куба. При этом полученные восемь вершин 3ПГК-4 обозначим буквой, соответствующей вершине исходного куба, но с индексом "Г" (от слова гиперкуб), то есть Aг, Bг, Cг, Dг, Eг, Fг, Gг, Hг.

Например, строим вершину Аг: по оси О+Zг от точки А надо отложить отрезок, равный ОА, ставим точку Аг, и так как ОА = a3/2, то ОАг = a3/2=aГ; строим вершину Fг : по оси О+Т от точки F откладываем отрезок, равный OF, ставим точку Fг; и так далее.

Итак, определили восемь вершин 3ПГК-4, причем координаты этих вершин легко определяются: так как эти вершины лежат непосредственно на осях, то они по этим осям имеют координату aг со знаком, соответствующим этой оси, а три остальные координаты – равны нулю.

Например, вершина Аг лежит на оси O+Zг , следовательно, вершина Аг имеет координаты: Т = 0, Xг = 0, Yг = 0, Zг = +aг; вершина Dг лежит на оси О-Т, следовательно, вершина Dг имеет координаты: Т = -aг , Хг = 0, Yг = 0, Zг = 0; и так далее.

Теперь через все эти восемь вершин проводим вспомогательные линии, параллельные оставшимся трем осям координат, - для каждой точки отдельно. Причем, учитывая, что положительные части осей на чертеже проведены сплошными линиями, а отрицательные части осей проведены пунктирными линиями, и то, что в этих вершинах именно эти три оси имеют значение ноль, надо вспомогательные линии, параллельные осям, проводить в соответствии их знаковым значениям: то есть эти точки являются границами между положительными и отрицательными частями этих вспомогательных линий.

Проведя все эти вспомогательные линии через точки Aг, Bг, Cг, Dг, Eг, Fг, Gг и Hг, на чертеже появятся шесть точек, в которых пересеклись по по четыре вспомогательных линии. Эти шесть точек и являются теми вершинами, лежащими на поверхности трехмерной проекции четырехмерного гиперкуба, в которых сходятся по четыре ребра, образующие четыре острых углов ромбов. Обозначим эти вершины: K, L, M, N, P и Q.

Итак, определены 14 вершин на поверхности трехмерной проекции четырехмерного гиперкуба. Вспомним, что две вершины (О1 и О2) этой проекции (3ПГК-4) совместились с центром О. Координаты всех 16-ти вершин трехмерной проекции четырехмерного гиперкуба сведены в таблицу 2.2.


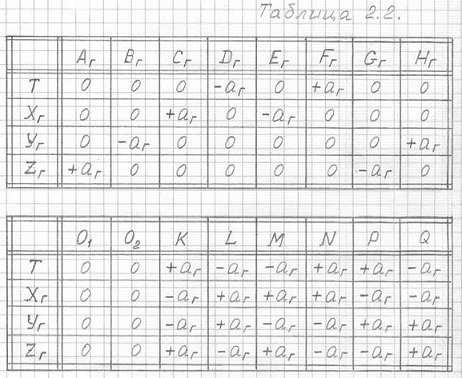
Таблица 2.2

Для того, чтобы проще было представить себе тело трехмерной проекции четырехмерного гиперкуба, рассмотрим промежуточный чертеж (рис. 2.4), где соединены только вершины, лежащие на поверхности 3ПГК-4.


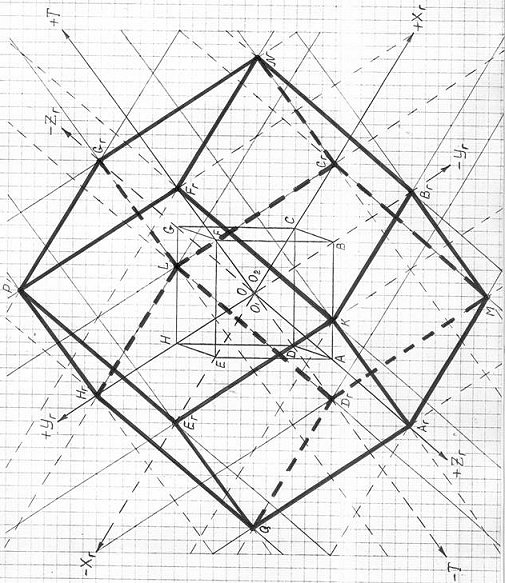
Рис. 2.4

А на рисунке 2.5 уже показаны и восемь внутренних ребер, и чертеж трехмерной проекции четырехмерного гиперкуба представлен в полном виде.


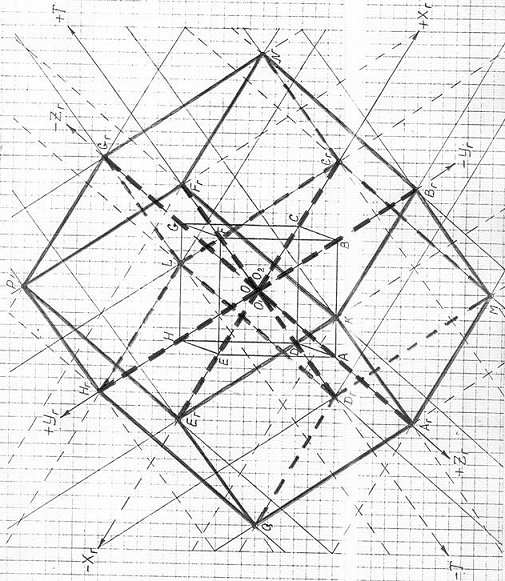
Рис. 2.5

Геометрические особенности трехмерной проекции четырехмерного гиперкуба (3ПГК-4)

Давайте рассмотрим геометрические особенности трехмерной проекции четырехмерного гиперкуба (3ПГК-4), построенного с помощью трехмерной проекции системы осей координат для четырехмерного измерения.

На рис. 2.6 представлен чертеж 3ПГК-4, начерченный только по вершинам 3ПГК-4, без осей координат и вспомогательных линий; для удобства масштаб чертежа уменьшен в два раза.


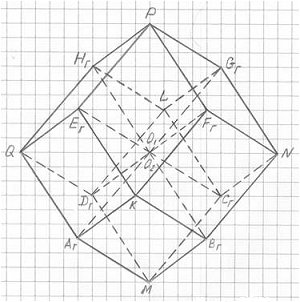
Рис. 2.6

Обратите внимание: через вершины трехмерной проекции четырехмерного гиперкуба (3ПГК-4) вписывается куб AгBгCгDгEгFгGгHг. Это очень важный факт для осмысления 3ПГК-4. Рисунок 2.7 дает очень наглядное представление о расположении вершин, ребер, граней 3ПГК-4. Смотрите: восемь внутренних ребер 3ПГК-4 (AгO, BгO, CгO, DгO, EгO, FгO, GгO и HгO) расположены на больших диагоналях вписанного в 3ПГК-4 куба, а четыре ребра 3ПГК-4 (EгP, FгP, GгP и HгP) образуют четырехугольную пирамиду PEгFгGгHг с основанием в виде квадрата EгFгGгHг, который является одной из шести граней вписанного в 3ПГК-4 куба. Причем, что очень важно, ребра этой пирамиды параллельны большим диагоналям вписанного в 3ПГК-4 куба, то есть PEг || GгAг, PFг || HгBг, PGг || EгCг и PHг || FгDг , при этом PEг = GгO, PFг = HгO, PGг = EгO и PHг = FгO (разумеется, что в точке О совмещены две вершины О1 и О2). А из этого следует, что пирамида PEгFгGгHг геометрически равна пирамиде OEгFгGгHг.


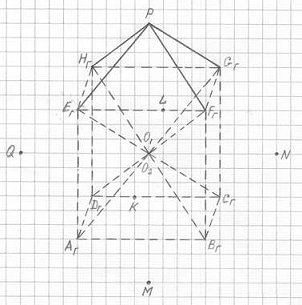
Рис. 2.7

Вершина Р является общей для шести граней-ромбов, равных между собой, причем четыре ромба (PEгKFг , PFгNGг, PGгLHг и PHгQEг) являются внешними гранями 3ПГК-4, а два ромба (PEгOGг и PFгOHг) являются внутренними гранями.

В рисунке 1.1 показано, что 3ПГК-4 пересекают пять параллельных между собой плоскостей, равноотстоящих друг от друга. Так вот, по рисункам 2.6 и 2.7 расположение этих пяти плоскостей определится следующим образом: вторая плоскость (РII) проходит через вершины Eг, Fг, Gг и Hг; четвертая плоскость (РIV) проходит через вершины Aг, Bг, Cг и Dг; третья плоскость (РIII) проходит через вершины Q, K, O1, O2, N и L; а первая (PI) и пятая (РV) плоскости проходят через вершины P и M соответственно.

Итак, на примере только одной пирамиды PEгFгGгHг определены некоторые очень важные свойства трехмерной проекции четырехмерного гиперкуба (3ПГК-4). Но если учесть, что остальные пять пирамид, построенные на других пяти гранях вписанного куба, геометрически равны пирамиде PEгFгGгHг, то, осмыслив безупречную симметрию и гармонию 3ПГК-4, можно только изумляться совершенству трехмерной проекции четырехмерного гиперкуба.

Совершенство трехмерной проекции четырехмерного гиперкуба (3ПГК-4) подтверждается и тем, что через вершины 3ПГК-4 можно построить не только вписанный куб AгBгCгDгEгFгGгHг, но и описанный куб A'B'C'D'E'F'G'H' – через вершины P, Q, K, N, L и M (см. рис. 2.8). А через вершины нашего вписанного куба, как известно математикам, легко вписывается еще одно "тело Платона" - тетраэдр. Кроме того, через шесть вершин 3ПГК-4 (P, Q, K, N, L и M) вписывается и еще одно "тело Платона" - октаэдр (см. рис. 2.9). Ребрами этого октаэдра являются 12 больших диагоналей ромбов – всех 12-ти внешних граней 3ПГК-4. А так как поверхность трехмерной проекции четырехмерного гиперкуба состоит из 12-ти ромбов, то эта геометрическая фигура называется еще ромбододекаэдром (см. рис. 2.8).


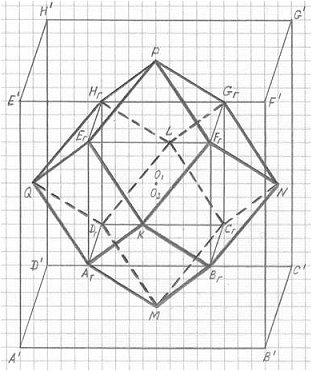
Рис. 2.8

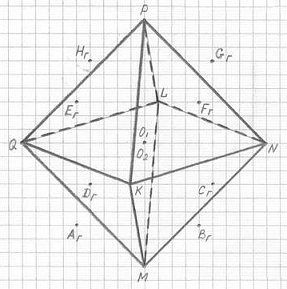
Рис. 2.9

Предлагаю вашему вниманию рисунки 2.10, 2.11, 2.12 и 2.13. Это одна и та же геометрическая фигура – трехмерная проекция четырехмерного гиперкуба (3ПГК-4). В этих чертежах нет искажений, я старалась выполнить их точно. Вершины, обведенные кружками, - это совмещенные вершины. Вот как легко можно начертить 3ПГК-4 (рис. 2.12, рис. 2.13).


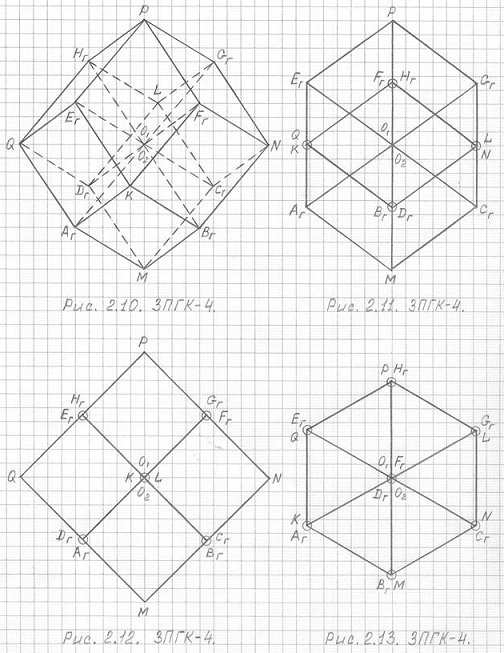
Рис. 2.10 - Рис. 2.13

Трехмерная проекция четырехмерного гиперкуба имеет 13 осей симметрии: семь осей симметрии проходят через 14 противоположных вершин, расположенных на поверхности 3ПГК-4 (PM, QN, LK, EгCг, FгDг, GгAг и HгBг), и шесть осей симметрии проходят через центры двенадцати противолежащих ромбов (граней), образующих поверхность 3ПГК-4.

Трехмерная проекция четырехмерного гиперкуба имеет 9 плоскостей симметрии: PGгCгMAгEг, PFгBгMDгHг, NCгDгQEгFг, NBгAгQHгGг, KAгDгLGгFг, KEгHгLCгBг, PNMQ, PKML и KNLQ.

Трехмерная проекция четырехмерного гиперкуба имеет три сферы с центром О1О2: большая сфера описывает вершины P, N, K, Q, L и M, средняя сфера описывает вершины Aг, Bг, Cг, Dг, Eг, Fг, Gг и Hг, а меньшая сфера вписывается через центры всех двенадцати граней (ромбов), образующих поверхность 3ПГК-4.

Об элементах, составляющих трехмерную проекцию четырехмерного гиперкуба

Математики давно просчитали, что четырехмерный гиперкуб (ГК-4) состоит из 16-ти вершин, 32-х ребер, 24-х граней и 8-и кубов. Предложенная мною трехмерная проекция четырехмерного гиперкуба (3ПГК-4) полностью соответствует этим расчетам (см. рисунки 2.5, 2.6, 2.10). Причем все ребра, все грани и все кубы абсолютно равны между собой (геометрически, а не физически).

Вершины 3ПГК-4

3ПГК-4 содержит 16 вершин: Aг, Bг, Cг, Dг, Eг, Fг, Gг, Hг, O1, O2, K, L, M, N, P и Q. Координаты по четырем осям (Xг, Yг, Zг и T) всех 16-ти вершин 3ПГК-4 указаны в таблице 2.2. 14 вершин расположены на поверхности 3ПГК-4, а две вершины (О1 и О2) совмещены в центре 3ПГК-4.

Совмещенные две вершины О1 и О2, я думаю, говорят нам о том, что (образно) наш трехмерный куб в четырехмерном пространстве под воздействием присущей этому пространству дополнительной, еще неведомой нам энергии не просто перемещается, а еще и вращается, вращается вокруг вершины (как, примерно, Земля, вращаясь вокруг своей оси, движется по орбите).

Говоря здесь о вершинах О1 и О2, совмещенных в одну точку О, будем иметь в виду, что все ниже перечисленные свойства вершин присущи индивидуально и вершинам О1 и О2, но совместившись в точке О, эти свойства количественно складываются.

Итак, каждая вершина 3ПГК-4 обладает следующими свойствами:

1) в каждой вершине 3ПГК-4 сходятся по четыре ребра. При этом: в вершинах K, L, M, N, P и Q сходятся 4 внешних ребра (например, в вершине K сходятся ребра KAг, KBг, KFг и KEг); в вершинах Aг, Bг, Cг, Dг, Eг, Fг, Gг и Hг сходятся по три внешних ребра и одно внутреннее ребро (например, в вершине Аг сходятся ребра AгK, AгM, AгQ и AгO); в вершинах О1 и О2 сходятся по 4 внутренних ребра, всего в точке О сходятся восемь внутренних ребер;

2) в каждой вершине 3ПГК-4 сходятся по шесть граней, то есть каждая вершина является общей вершиной для шести граней, например: а) в вершине Р сходятся грани PEгKFг, PFгNGг, PGгLHг, PHгQEг, PEгO1Gг и PFгO1Hг ; б) в вершине Eг сходятся грани EгQAгK, EгKFгP, EгPHгQ , EгQDгO2, EгO1GгP и EгKBгO2 ; в) в вершине О (О1 и О2) сходятся все 12 внутренних граней: AгOFгK, AгOHгQ, AгOCгM, BгOEгK, BгODгM, BгOGгN, CгOHгL, CгOAгM, CгOFгN, DгOGгL, DгOEгQ и DгOBгM;

3) в каждой вершине 3ПГК-4 сходятся по 4 куба. Например: а) в вершине Р сходятся 4 куба: PHгQEгFгO1AгK, PEгKFгGгO1BгN, PFгNGгEгKBгO1 и PGгLHгEгO1DгQ ; б) в вершине Aг сходятся 4 куба: AгKEгQO2FгPHг, AгMBгKO2CгNFг, AгQDгMKEгO2Bг и AгQDгMO2HгLCг; в) как видим, центр О, т.е. точка совмещенных вершин О1 и О2 , является общей вершиной для всех восьми кубов 3ПГК-4.

Ребра 3ПГК-4

Ко всему, что сказано выше о ребрах 3ПГК-4, можно добавить, что ребра 3ПГК-4 обладают еще и следующими свойствами:

1) каждое ребро 3ПГК-4 принадлежит трем граням. Например: а) ребро PEг принадлежит граням PEгQHг, PEгKFг и PEгO1Gг; б) ребро AгK принадлежит граням AгKBгM, AгKFгQ и AгKFгO2; в) ребро О2Аг принадлежит граням O2AгQHг, O2AгMCг и O2AгKFг;

2) каждое ребро 3ПГК-4 принадлежит трем кубам. Например: а) ребро PEг принадлежит кубам PEгQHгGгO1DгL, PEгKFгHгQAгO1 и PEгO1GгFгKBгN; б) ребро AгK принадлежит кубам AгKBгMQEгO2Dг, AгKEгQO1FгPHг и AгKFгO2MBгNCг; в) ребро О2Аг принадлежит кубам O2AгQHгFгKEгP, O2AгMCгHгQDгL и O2AгKFгCгMBгN.

Единичная грань 3ПГК-4

Гранью трехмерной проекции четырехмерного гиперкуба (3ПГК-4) является ромб (см. рис. 2.15, 2.17).

Определимся с размерностью геометрических параметров ромба PEгKFг. Здесь нам очень помогут геометрические параметры вписанного в 3ПГК-4 куба AгBгCгDгEгFгGгHг. Примем, что длина ребра ромба PEгKFг, а следовательно, и самой трехмерной проекции четырехмерного гиперкуба (3ПГК-4) равна величине а; длину малой диагонали EгFг ромба обозначим через d, а длину большой диагонали PK ромба обозначим через D.


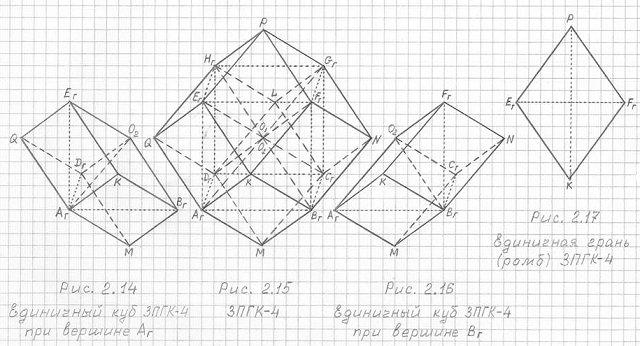
Рис. 2.14 - Рис. 2.17

Из чертежа рис. 2.15 нетрудно заметить, что длина ребра а 3ПГК-4, а следовательно, и ромба, равна половине большой диагонали вписанного в 3ПГК-4 куба AгBгCгDгEгFгGгHг; малой диагональю (EгFг) ромба является ребро этого вписанного куба, а большой диагональю ромба (PK=D) является диагональ боковой грани (квадрата) этого вписанного куба.

Из вышесказанного, пользуясь теоремой Пифагора, можно написать: AгCг = EгFг·3, то есть

2 · a = d 3 (2.5)

Результаты простых расчетов взаимосоотношений главных определяющих параметров ромба (грани 3ПГК-4) a, d и D приведены в таблице 2.3.


Таблица 2.3

Результаты расчетов, приведенные в таблице 2.3, потребуются для вычисления других геометрических параметров 3ПГК-4.

Гранью трехмерной проекции гиперкуба любого n-мерного измерения (3ПГК-4, 3ПГК-5, 3ПГК-6, ..., 3ПГК-n) является ромб, только ромб. Очень важной геометрической характеристикой ромба является соотношение его большой и малой диагоналей (D/d). В многомерной геометрии это соотношение для каждого измерения строго определенно и неизменно. Так, в квадрате (символ второго измерения) соотношение его диагоналей равно единице (1); грань трехмерного куба также сохраняет это соотношение (1), так как его гранью является квадрат. Невозможно хотя бы слегка изменить соотношение диагоналей в квадрате – иначе квадрат теряет свое звание.

В 3ПГК-4 отношение большей диагонали ромба (грани) к меньшей определится:

D d = 2 ≈ 1,414 (2.6)

Забегая вперед скажем, что в 3ПГК-5 отношение большей диагонали ромба (грани) к меньшей составляет:

D d = 1 + 5 2 ≈ 1,618 (2.7)

Ко всему, что сказано о единичных гранях (ромбах) 3ПГК-4 в этой главе, надо добавить, что каждая единичная грань 3ПГК-4 принадлежит одновременно двум кубам. Например: 1) грань PHгQEг принадлежит кубу PHгQEгGгLDгO1 и кубу PHгQEгFгO1AгK; 2) грань PEгKFг принадлежит кубу PEгKFгHгQAгO1 и кубу PEгKFгGгO1BгN.

Единичный куб 3ПГК-4

Как видно из чертежей рисунков 2.14, 2.15 и 2.16, единичные кубы трехмерной проекции четырехмерного гиперкуба (3ПГК-4) можно построить не только при вершинах Аг и Вг вписанного в 3ПГК-4 куба AгBгCгDгEгFгGгHг, но и при остальных шести вершинах этого вписанного куба. Таким способом легко определить все восемь (8) единичных кубов, образующих 3ПГК-4.

Геометрические особенности единичного куба 3ПГК-4

Чтобы понять, как выглядит единичный куб 3ПГК-4, представьте себе трехмерный куб с длиной ребра а. Этот куб имеет 4 больших диагонали, равных между собой, длина которых равна a·3. Теперь одну из этих больших диагоналей уменьшите до величины ребра куба (то есть до величины а) так, чтобы три других диагонали, увеличившись при этом по длине, были равны между собой. Вот вы и получили единичный куб 3ПГК-4.

Что-то мне не приходит на ум, как правильно назвать эту фигуру. Ромбогексаэдр? Или просто четырехгранной призмой? Поправьте, пожалуйста, если я ошиблась.

Определим объем единичного куба BгNCгMKFгO2Aг трехмерной проекции четырехмерного гиперкуба Vе.к. (см. рис. 2.18).


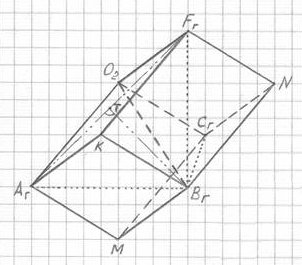
Рис. 2.18

Так как по определению единичный куб 3ПГК-4 – это четырехгранная призма, то ее объем определится как произведение площади основания этой призмы на высоту этой призмы. Примем за основание этой призмы грань BгNCгM. Площадь единичной грани 3ПГК-4 Sе.г., которой является ромб BгNCгM , равна половине произведения диагоналей этого ромба, то есть:

S е.г. = D · d 2 (2.8)

Из таблицы 2.3 возьмем значение D через d: D=d·2 и выразим Sе.г. только через d:

S е.г. = d · 2 · d 2 = d 2 · 2 2 (2.9)

Высотой h в этой четырехгранной призме является отрезок ВгТ, то есть h=BгT. Из равнобедренного прямоугольного треугольника AгBгFг (где AгBг = BгFг = d и AгFг = D) легко определить, что отрезок BгT = h равен 1/2·AгFг и является собственно половиной диагонали BгEг = D (см. рис. 2.15) в грани (квадрате) AгBгFгEг вписанного в 3ПГК-4 куба. Следовательно,

h = D 2 = d · 2 2 (2.10)

Тогда объем четырехгранной призмы BгNCгMKFгO2Aг, то есть объем единичного куба 3ПГК-4 Vе.к. определится:

V е.к. = S е.г. · h = d 2 · 2 2 · d · 2 2 = d 3 2 (2.11)

Замечательно, что величина d3 - это объем вписанного в 3ПГК-4 куба AгBгCгDгEгFгGгHг, ребро которого обозначено через d.

Итак, вычислено, что объем единичного куба 3ПГК-4 Vе.к. равен половине объема вписанного в 3ПГК-4 куба.

Объем всех восьми единичных кубов 3ПГК-4 соответственно определится:

8 · V е.к. = 8 · d 3 2 = 4 · d 3 (2.12)

Определим объем тела трехмерной проекции четырехмерного гиперкуба V3ПГК-4. Вернемся к рис. 2.7 и 2.15.

При обсуждении чертежа на рис. 2.7 было доказано, что четырехугольная пирамида PEгFгGгHг геометрически равна пирамиде O1EгFгGгHг. При этом следует иметь в виду, что пирамида PEгFгGгHг – внешняя по отношению к вписанному в 3ГПК-4 кубу и таких внешних пирамид – шесть, но ведь и сам вписанный в 3ПГК-4 куб состоит из шести внутренних четырехугольных пирамид. А так как все двенадцать пирамид геометрически равны между собой, то общий объем шести внешних пирамид также равен объему вписанного в 3ПГК-4 куба, следовательно, объем 3ПГК-4 равен удвоенному объему вписанного в него куба, то есть:

V 3ПГК-4 = 2 · d 3 (2.13)

Это самый легкий и очевидный способ определения объема 3ПГК-4. Есть и другие способы.

Объем восьми единичных кубов (4d3) больше объема самой трехмерной проекции четырехмерного гиперкуба (2d3) ровно в два раза. Почему? Давайте разберемся, как размещены единичные кубы в теле 3ПГК-4 и между собой.

Чтобы понять, как размещены единичные кубы в теле 3ПГК-4, рассмотрим чертежи рисунка 2.19.

Из тела 3ПГК-4 (рис. 2.19, а) выделен единичный куб при вершине Bг (BгNCгMKFгO2Aг) (рис. 2.19, б), который, в свою очередь, состоит из трех геометрически равных между собой четырехугольных пирамид с общей вершиной О2: O2BгKAггM, O22BгNFгK и O2BгNCгM (рис. 2.19, в, г, д). Основаниями этих пирамид служат находящиеся на поверхности 3ПГК-4 грани (ромбы) выделенного единичного куба. Соблюдаются также следующие равенства боковых ребер этих пирамид: O2Bг = O2Aг = O2Fг = O2Cг = а и O2K = O2M = O2N = d. Все эти пирамиды имеют ту же высоту h, что и сам единичный куб, то есть четырехугольная призма.

Вычислим объем этой пирамиды Vпир. с помощью формул (2.9) и (2.10):

V пир = 1 3 · S е.г. · h = 1 3 · d 2 · 2 2 · d · 2 2 = d 3 6 (2.14)

что подтверждает, что объем пирамиды в три раза меньше объема единичного куба.

Так как внешних граней в 3ПГК-4, образующих ее поверхность S3ПГК-4, 12 и каждая из этих 12-ти граней является основанием пирамиды с вершиной в точке О, то суммарный объем всех этих 12-ти пирамид также определит объем 3ПГК-4:

V 3ПГК-4 = 12 · V пир = 12 · d 3 6 = 2 d 3 (2.15)


Вот второй способ определения объема 3ПГК-4.

Площадь поверхности 3ПГК-4 определится таким образом:

S 3ПГК-4 = 12 · S е.г. = 12 · d 2 · 2 2 = 6 · d 2 · 2 (2.16)

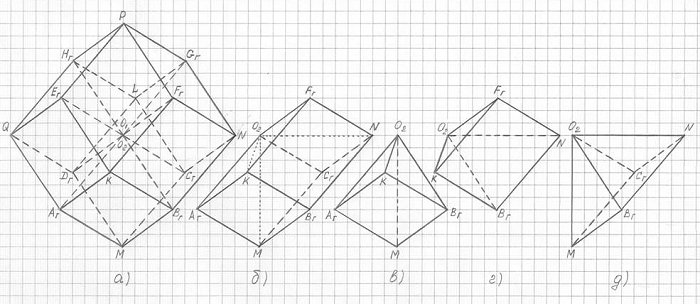
Рис. 2.19

Но вернемся к теме обсуждения.

Выделенный при вершине Вг единичный куб BгNFгKMCгO2Aг каждой третью своей делит (совмещает) свой объем с тремя единичными кубами, расположенными при вершинах Aг, Fг и Cг:

1) c единичным кубом AгMDгQKBгO2Eг – совмещенный объем в виде пирамиды O2BгKAгM;

2) с единичным кубом FгNGгPKBгO1Eг – совмещенный объем в виде пирамиды O2BгNFгK ;

3) с единичным кубом CгMBгNLDгO2Gг – совмещенный объем в виде пирамиды O2BгNCгM. Следует заметить, что в вписанном в 3ПГК-4 кубе AгBгCгDгEгFгGгHг вершины Aг, Fг и Cг являются ближайшими к вершине Вг.

Таким образом, доказано, что каждый единичный куб 3ПГК-4 каждой третью своего объема совмещает свое пространство (объем) с другими тремя близлежащими единичными кубами.

Вот поэтому суммарный объем всех восьми единичных кубов 3ПГК-4 (8·Vе.к.=4·d3) больше объема самой 3ПГК-4 (V3ПГК-4=2·d3) в два раза.

Еще два свойства единичных кубов 3ПГК-4:

1) каждый единичный куб 3ПГК-4 имеет по одной грани, общей с шестью из семи других единичных кубов. Так, единичный куб BгNCгMKFгO2Aг не имеет общей грани только с единичным кубом HгQEгPLDгO1Gг, при этом заметим, что вершины в этих единичных кубах Bг и Hг, N и Q, Cг и Fг, M и P, K и L , Fг и Dг, Aг и Gг – диаметрально противоположные; и только восьмая пара вершин О1 и О2 в этих единичных кубах является одной совмещенной вершиной.

2) все восемь единичных кубов 3ПГК-4 имеют общую вершину, в которой совмещены две вершины - О1 и О2.

Результаты расчетов основных геометрических параметров 3ПГК-4, выраженные через элементы ромба (единичной грани 3ПГК-4), представлены в таблице 2.4.


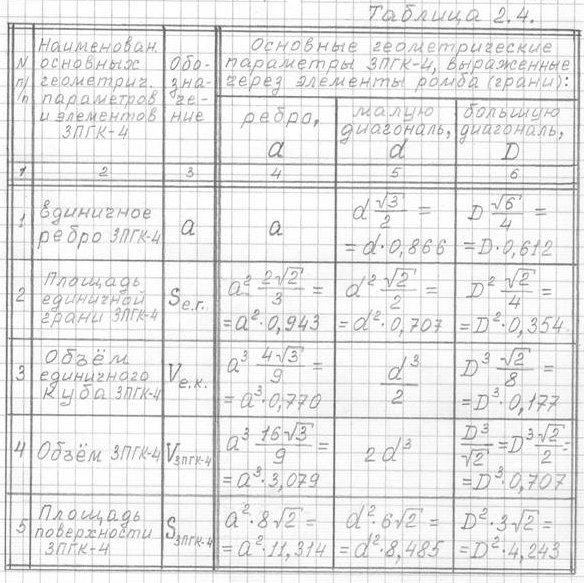
Таблица 2.4
© Идея и дизайн Влада Алексеева, 2001-2024. (impossible.world@gmail.com) | Политика конфиденциальности
Перепечатка материалов сайта приветствуется со ссылкой на сайт.
Если у вас есть изображения невозможных фигур, неопубликованных на сайте, пожалуйста, присылайте их мне.