Многомерная геометрия
Давайте вновь обратимся к рис. 1.1, где на одной странице начерчены проекции символов семи измерений во фронтальной проекции.
Профильные проекции этих геометрических фигур почти аналогичны фронтальным, а горизонтальные проекции будут представлены ниже.
Создав из трубочек и лески модели трехмерных проекций четырехмерного гиперкуба (3ПГК-4) и пятимерного гиперкуба (3ПГК-5), автором был разработан принцип, метод создания моделей всех последующих (3ПГК-6), (3ПГК-7), ..., (3ПГК-n).
Осмысление уже имеющихся в распоряжении автора моделей куба, 3ПГК-4 и 3ПГК-5 позволило выявить очень важную (главную!) особенность трехмерных моделей и куба, поставленного в "интересное положение", и всех 3ПГК-n: все они в первом и в последнем "ярусах" (см. Гл. 1) представлены в виде правильных n-угольных пирамид, где "n" соответствует n-мерности данной геометрической фигуре – данного n-мерного символа измерения.
Начнем с нашего куба – геометрического символа трехмерного измерения. Рис. 1.2 (Гл. 1) более наглядно показывает верхнюю правильную треугольную пирамиду ABFD, расположенную (заключенную) в первом ярусе между параллельными плоскостями РI и РII [рис. 1.2 (б)], и нижнюю правильную треугольную пирамиду HCEG, расположенную (заключенную) в последнем, третьем "ярусе" между параллельными плоскостями РIII и PIV [рис. 1.2 (г)].
Выбрав любой ракурс изображения (фронтальную, горизонтальную, профильную прямоугольные проекции или общий вид) правильной треугольной пирамиды ABFD, мы по трем боковым ребрам AB, AF и AD этой пирамиды, которые являются собственно ребрами куба ABCDEFGH, можем построить этот куб именно в данном выбранном ракурсе (см. рис.3.1).
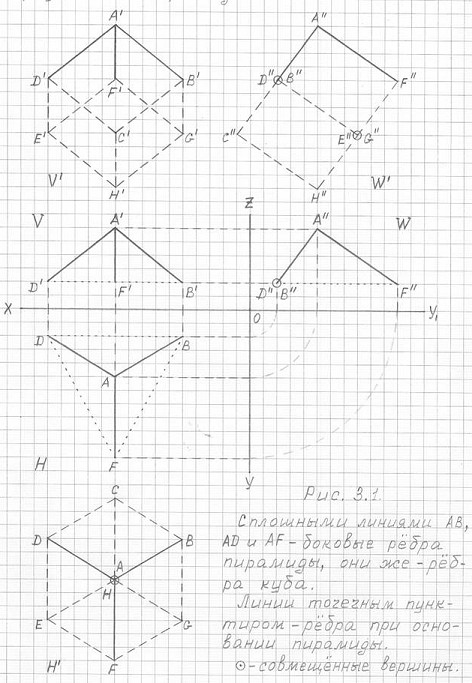
Рис. 3.1
Построение горизонтальной (H') и вертикальной (V') и профильной (W') проекций куба ABCDEFGH по соответствующим проекциями правильной треугольной пирамиды ABDF.
Требуется ли пояснять рис. 3.1? Думаю, любой геометр по трем ребрам куба, сходящимся в одной вершине, сможет достроить сам куб. И не важно, в каком ракурсе изображены эти ребра.
Например, я стараюсь рассмотреть и такой ракурс (т.н. "уклон"), когда геометрические символы n-мерного измерения (квадрат, куб, 3ПГК-4, 3ПГК-5, 3ПГК-6 и т.д.) рассматриваются в ракурсе наибольшего совмещения вершин (и ребер соответственно).
Этот ракурс достигается, когда направление линии "уклона" параллельно одному из боковых ребер "исходной" n-угольной пирамиды: таким образом, это боковое ребро пирамиды и, соответственно, все остальные параллельные ему ребра этого n-мерного геометрического символа на чертеже проецируются в виде точки – совмещенной вершины.
Именно в таком ракурсе выполнены чертежи куба (рис. 3.2), 3ПГК-4 (рис. 3.11), 3 ПГК-5, 3ПГК-6 (рис. 3.24), 3ПГК-7 (рис. 3.36). Этот ракурс автор я еще называю: "оригинальный ракурс".
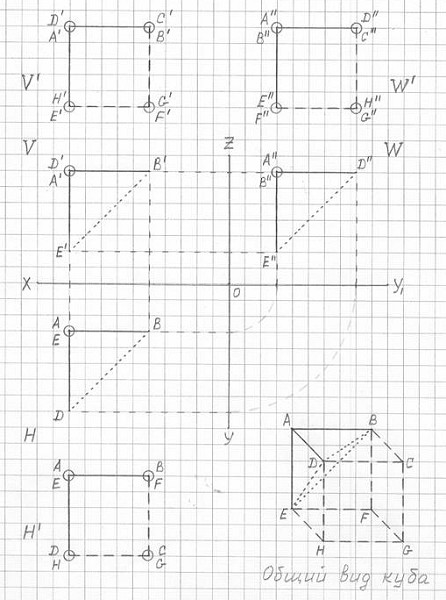
Рис. 3.2
Построение горизонтальной (H') и вертикальной (V') и профильной (W') проекций куба ABCDEFGH по соответствующим проекциями правильной треугольной пирамиды ABDE в ракурсе наибольшего совмещения вершин
Почему при черчении столь хорошо известного куба я уделяю большое внимание совмещению вершин и ребер? – потому что куб проще и более понятен для осмысления.
А вот при черчении более сложных геометрических фигур – 3ПГК-4, 3ПГК-5, 3ПГК-6, и т.д., в которых количество вершин и ребер значительно больше, чем в кубе, вероятность совмещения вершин и ребер значительно возрастает, а точнее – в большинстве случаев избежать совмещения вершин и ребер практически невозможно.
В этой главе требуются расчетные данные количества единичных элементов, составляющих 3ПГК-n. Поэтому здесь необъодимо привести таблицу 2 из моих прошлых работ.
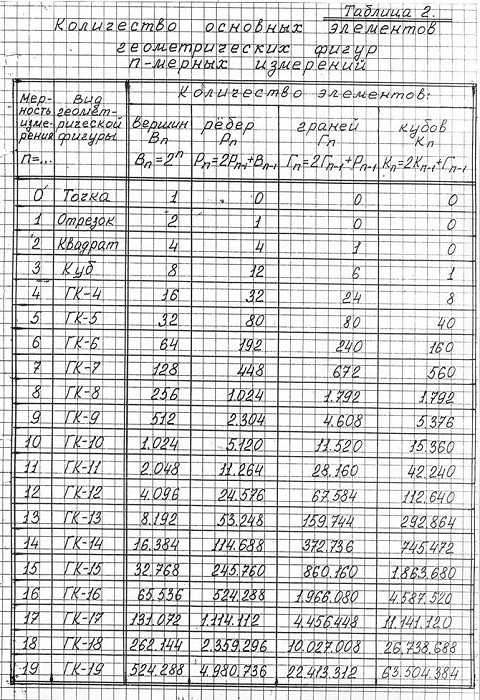
Главные принципы и особенности строения трехмерных проекций n-мерных гиперкубов
Прежде чем приступить к построению (черчению) трехмерных проекций n-мерных гиперкубов, оговорим некоторые закономерности, особенности, главные принципы строения этих геометрических фигур.
Предлагаю вашему вниманию главные геометрические свойства и особенности трехмерных проекций всех n-мерных гиперкубов (3ПГК-n) и разработанные принципы, методы, правила создания, построения и черчения трехмерных проекций n-мерных гиперкубов (3ПГК-n).
1. Во всех n-мерных гиперкубах, а также и в их трехмерных проекциях, в каждой вершине сходятся по n ребер. То есть: в каждой из 16-ти вершин 3ПГК-4 сходятся по 4 ребра, в каждой из 32-х вершин 3ПГК-5 сходятся по 5 ребер, в каждой из 64-х вершин 3ПГК-6 сходятся по 6 ребер, и т.д.
2. Во всех трехмерных проекциях n-мерных гиперкубов (см. рис. 1.1) в первом "ярусе" (то есть между параллельными плоскостями РI и РII) и в последнем "ярусе" (между параллельными плоскостями Рn и Рn+I) находятся по n ребер, сходящихся в верхней вершине, расположенной в плоскости РI, и в нижней вершине, расположенной в плоскости Рn+I.
Эти n ребер можно (и нужно) представить как боковые ребра правильной n-угольной пирамиды. Эти пирамиды назовем "исходными" пирамидами.
Вот это и есть очень важная (главная) для построения и черчения трехмерных проекций n-мерных гиперкубов особенность:
а) в любой 3ПГК-n в первом и в последнем "ярусах" заключена часть тела 3ПГК-n в виде правильной n-угольной пирамиды;
б) по построенной "исходной" правильной n-угольной пирамиде в любом ракурсе, в любой проекции можно построить (начертить) и 3ПГК-n в выбранных ракурсах и проекциях.
3. Любое ребро n-мерного гиперкуба (ГК-n), а также его трехмерной проекции (3ПГК-n) геометрически равно по длине и параллельно одному из n боковых ребер т.н. "исходной" правильной n-угольной пирамиды, расположенной в первом или последнем "ярусе" ГК-n или 3ПГК-n.
4. Отрезок прямой в теле 3ПГК-n, соединяющий вершины, расположенные в параллельных плоскостях РI и Рn+I, т.е. вершины верхней и нижней "исходных" правильных n-угольных пирамид (см. рис. 1.1), перпендикулярен этим плоскостям РI и Рn+I и является главной осью симметрии 3ПГК-n.
5. В n-мерных гиперкубах, где n – четное число, а также в их трехмерных проекциях (т.е. в 3ПГК-4, 3ПГК-6, 3ПГК-8, 3ПГК-10, и т.д.), обязательно существуют геометрически обусловленные совмещенные (сдвоенные) вершины, расположенные в точках пересечения визуально проведенной главной оси симметрии 3ПГК-n с визуально обозначенными на рис. 1.1 параллельными плоскостями: РIII - в 3ПГК-4; РIII и РV - в 3ПГК-6; РIII , РV и РVII - в 3ПГК-8, и т.д.
В этих геометрически обусловленных совмещенных (сдвоенных) вершинах 3ПГК-n соответственно сходятся по 2n ребер, вот почему я написала фразу: "... в большинстве случаев избежать совмещения вершин и ребер практически невозможно".
6. При изображении 3ПГК-n (черчении или фотографировании их моделей) в разных ракурсах возможны визуальные совмещения любых вершин, а также визуальные совмещения ребер, граней и даже кубов.
Построение (черчение) трехмерных проекций четырехмерного гиперкуба (3ПГК-4)
На рис. 3.3 представлено построение горизонтальной (H'), фронтальной (V') и профильной (W') проекций четырехмерного гиперкуба (3ПГК-4) по соответствующим проекциям "исходной" правильной четырехугольной пирамиды.
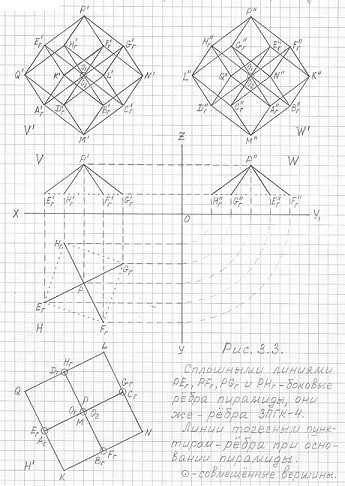
Рис. 3.3
Построение горизонтальной (H') и вертикальной (V') и профильной (W') проекций четырехмерного гиперкуба (3ПГК-4) по соответствующим проекциям правильной четырехугольной пирамиды PгEгFгGгHг
А на рис. 3.4 показана последовательность построения (черчения) на рис. 3.3 фронтальной (VI) проекции 3ПГК-4 по фронтальной (V) проекции "исходной" правильной четырехугольной пирамиды.
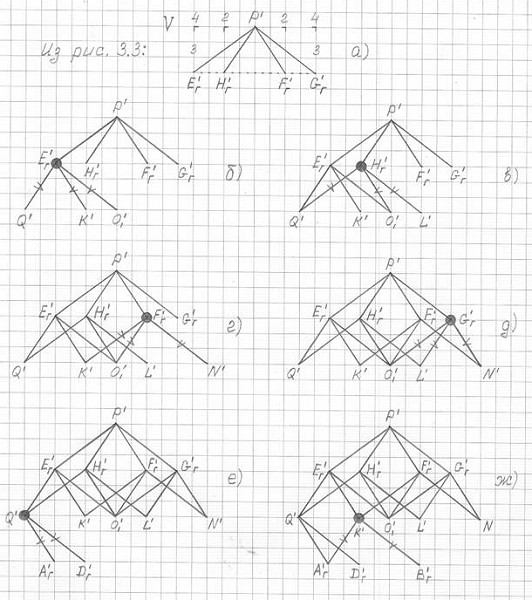
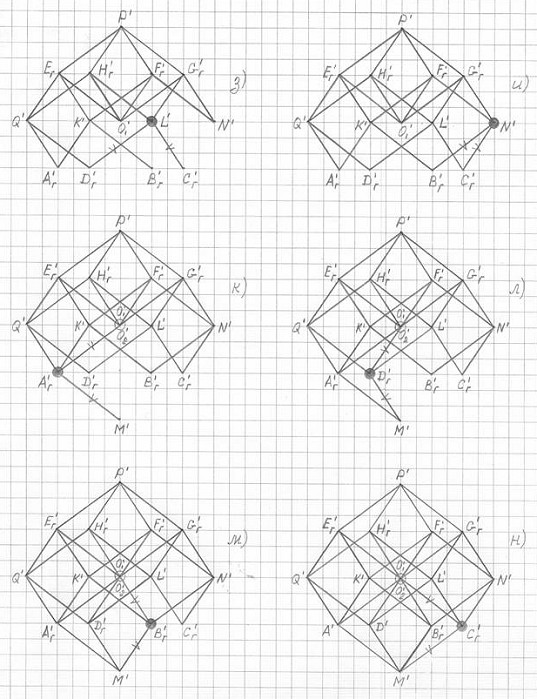
Рис. 3.4
Последовательность построения (черчения) фронтальной проекции VI 3ПГК-4 по фронтальной проекции V правильной четырехугольной пирамиды P'E'гF'гG'гH'г
кружком обозначены вершины проекции V' 3ПГК-4, к которым в данном чертеже (б,в,г,...,н) были потроены недостающие ребра проекции V пирамиды.
Данный метод (принцип, способ) построения (черчения) горизонтальной, фронтальной и профильной проекций 3ПГК-4 состоит в том, что в соответствующих им горизонтальной, фронтальной и профильной проекциях "исходной" пирамиды к каждой вершине последовательно достраиваются еще три недостающих боковых ребра этой пирамиды.
Предлагаю вашему вниманию важный для понимания 3ПГК-4 ракурс (рис. 3.5.). В этом ракурсе в "исходной" пирамиде 3ПГК-4 во фронтальной и профильной проекциях визуально совмещены две пары боковых ребер пирамиды, в результате чего в чертежах фронтальной, профильной и даже горизонтальной проекциях 3ПГК-4 произошло визуальное совмещение пяти пар вершин, и соответственно, шестнадцати пар ребер!
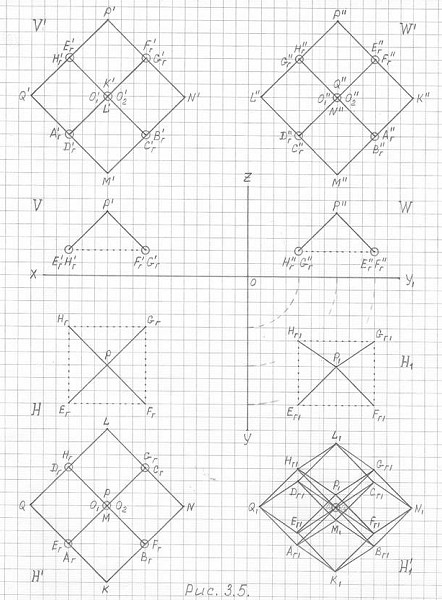
Рис. 3.5
Построение горизонтальной (H'), фронтальной (V') и профильной (W') проекций трехмерной проекции четырехмерного гиперкуба 3ПГК-4 по соответствующим проекциям правильной четырехугольной пирамиды P'E'гF'гG'гH'г в выбранном ракурсе.
Для наглядности - в проекциях H' и H'1 небольшое смещение ракурса
куржками отмечены совмещенные вершины.
В этом же рис. 3.5 для наглядности, т.е. лучшего понимания расположения вершин и ребер проекций 3ПГК-4, дополнительно начерчены в горизонтальных проекциях "исходная" пирамида и 3ПГК-4 в слегка измененном ракурсе.
Этот способ построения (черчения) проекций 3ПГК-n – легкое, очень небольшое изменение ракурса – очень удобно применять, особенно при построении горизонтальных проекций 3ПГК-4.
Все горизонтальные проекции 3ПГК-n в идеально правильном исполнении чертежа, построенные (начерченные) с помощью соответствующей горизонтальной проекции "исходной" правильной n-угольной пирамиды, обязательно имеют совмещения вершин (визуальные или реальные, фактические – геометрически обусловленные) и ребер (только визуально полностью или частично совмещенные).
В самих n-мерных гиперкубах (ГК-n) могут быть совмещены вершины, но не может быть совмещенных ребер, граней, кубов.
Я не рекомендовала бы вам, уважаемые геометры, сразу приступать к черчению идеально правильных горизонтальных проекций 3ПГК-n, потому что очень трудно осмыслить как, в какой последовательности происходит совмещение вершин, ребер и даже граней в чертеже.
Вот поэтому автор сначала выбирает горизонтальную проекцию "исходной" правильной n-угольной пирамиды в слегка измененном ракурсе и последовательно, как показано на рис. 3.6, строит (чертит) соответствующую проекцию 3ПГК-n.
Заметьте, что при последовательном черчении проекций 3ПГК-4 на рис. 3.6 автор, так сказать, идет по крайним вершинам.
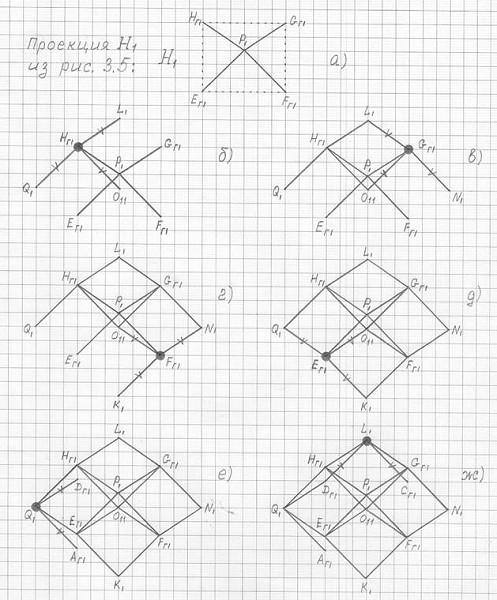
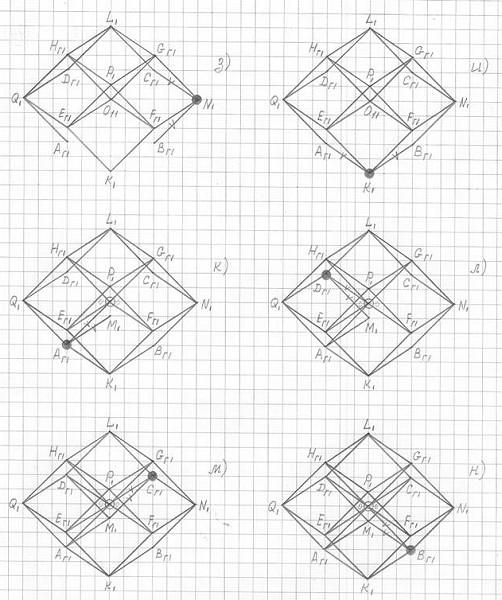
Рис. 3.6
Последовательность построение (черчения) проекции H'1 3ПГК-4 с рис. 3.5 (слегка измененого ракурса горизонтальной проекции H') по соответствующей проекции H1 правильной четырехугольной пирамиды P'E'гF'гG'гH'г. Затемненными кружками отмечены вершины, к которым в данном чертеже (б, в, с, ..., н) были построены недостающие рёбра; эти ребра отмечены "галочками".
Представляет интерес следующий ракурс изображения (черчения) фронтальной (V') и профильной (W') проекций 3ПГК-4 на рис. 3.7.
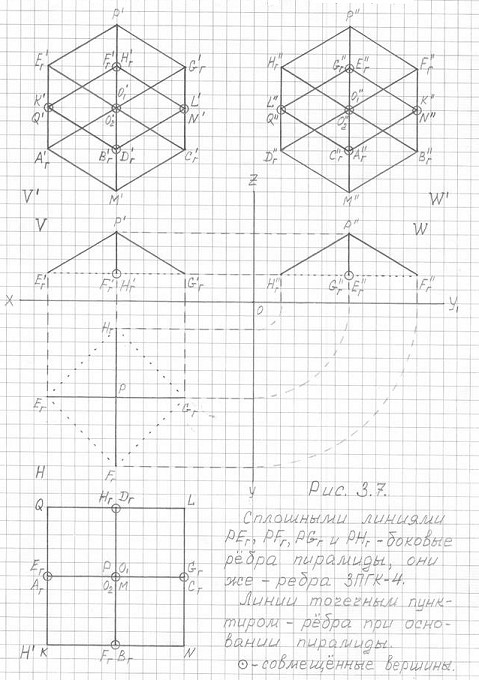
Рис. 3.7
Построение горизонтальной (H'), вертикальной (V') и профильной (W') проекций трехмерной проекции четырехмерного гиперкуба 3ПГК-4 по соответствующим проекциям правильной четырехугольной пирамиды PEгFгGгHг.
Для осмысления, например, фронтальной проекции 3ПГК-4 достаточно слегка изменить ракурс (см. рис. 3.8) и фронтальная проекция "исходной" пирамиды (а) на рис. 3.8 примет вид (а1).
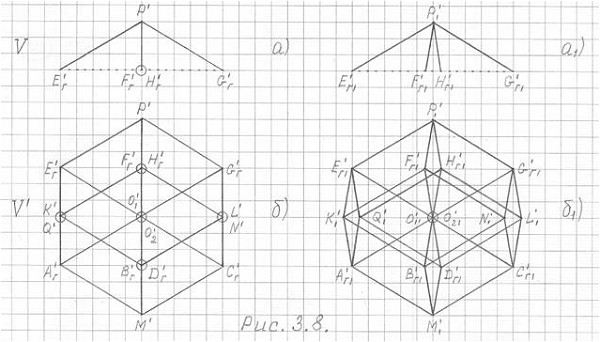
Рис. 3.8
а) и б) - из рис. 3.7 - фронтальные проекции исходной пирамиды (V) и 3ПГК-4 (V').
а1) и б1) - то же, в слегка измененом ракурсе для наглядности. "Кружочками" отмечены совмещённые вершины.
На рисунках 3.9, 3.10 и 3.11 вашему вниманию предлагаются чертежи трехмерной проекции четырехмерного гиперкуба (3ПГК-4) в наиболее важных ракурсах. Причем для наглядности и лучшего понимания расположения на чертежах вершин и ребер 3ПГК-4 в этих рисунках справа представлены чертежи 3ПГК-4 в слегка измененном ракурсе.
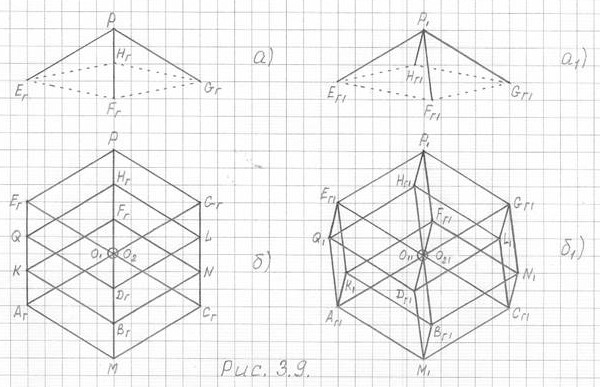
Рис. 3.9
б) - чертеж 3ПГК-4 в оригинальном ракурсе,
построенный с помощью проекции пирамиды а)
б1) - для наглядности, то же в слегка измененном ракурсе.
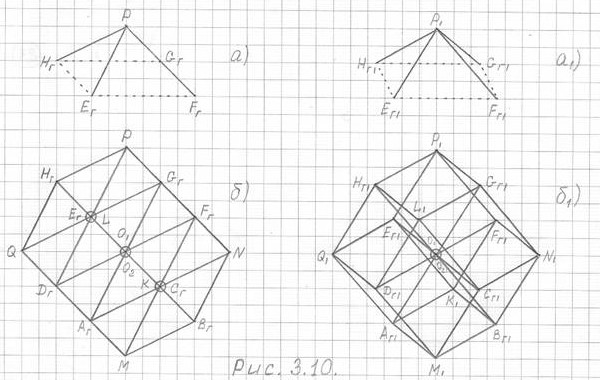
Рис. 3.10
б) - чертеж 3ПГК-4 в оригинальном ракурсе,
построенный с помощью проекции пирамиды а)
б1) - для наглядности, то же в слегка измененном ракурсе.
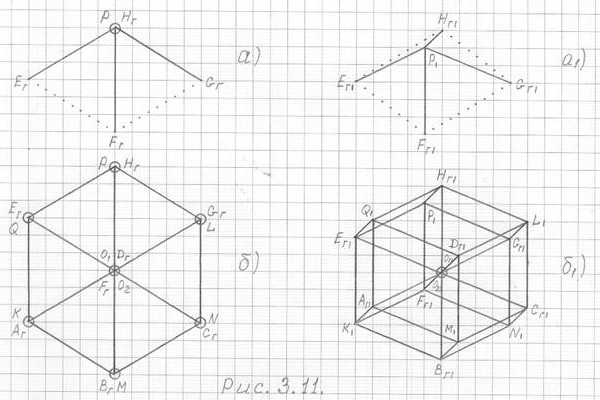
Рис. 3.11
б) - чертеж 3ПГК-4 в оригинальном ракурсе,
построенный с помощью проекции пирамиды а)
б1) - для наглядности, то же в слегка измененном ракурсе.
Глядя на чертежи, возможно, вам трудно будет поверить, что это действительно чертежи 3ПГК-4. Но я из трубочек и лески создала несколько экземпляров моделей 3ПГК-4 и 3ПГК-5 и развесила их по всей квартире, чтобы они везде были на виду, и поэтому я имею возможность рассматривать их в разных ракурсах.
Вы можете сами начертить "исходную" правильную n-угольную пирамиду 3ПГК-n в абсолютно любом ракурсе и, пользуясь тем или иным методом, начертить соответствующую проекцию 3ПГК-n. И вовсе не обязательно в одном чертеже классически строить одновременно горизонтальную, фронтальную и профильную проекции, - профессиональному геометру по виду начерченной "исходной" правильной n-угольной пирамиды 3ПГК-n уже понятно, в каком ракурсе начерчена проекция 3ПГК-n.
О внешнем виде всех 3ПГК-n
Вот аналогия: все 3ПГК-n как на их чертежах, так и в самих моделях, своей внешней геометрической формой напоминают "юлу" (или волчок). И чем выше измерение, тем все более и более 3ПГК-n напоминает форму "юлы".
В идеально построенных чертежах 3ПГК-n, где n≥5, существует только одна горизонтальная проекция 3ПГК-n, фронтальных и профильных проекций – сколь угодно много, а проекций в ракурсах под определенным углом зрения – бесчисленное множество.
Итак, чтобы построить горизонтальную проекцию 3ПГК-n, надо сначала построить горизонтальную проекцию ее "исходной" правильной n-угольной пирамиды, то есть построить правильный n-угольник. – Всего-то!
Еще раз обращаю ваше внимание на факт, что на тетрадном листе бумаги "в клетку" через вершины квадратных "клеток", кроме самого квадрата, невозможно построить все остальные правильные многоугольники (треугольник, пятиугольник, шестиугольник, ..., десятиугольник, ..., и т.д.).
Автор каждое ребро многоугольника в моих чертежах рассматривает как гипотенузу и проверяет ее теоремой Пифагора. Пытаясь построить эти правильные многоугольники "по вершинам "клеток"", он добивается наименьшей погрешности в чертежах.
Я каждое ребро многоугольника в моих чертежах рассматриваю как гипотенузу и проверяю ее теоремой Пифагора. Пытаясь построить эти правильные многоугольники "по вершинам "клеток"", я добиваюсь наименьшей погрешности в чертежах.
Казалось бы, черчение 3ПГК-n "по вершинам клеток" - недостаток. Но этот "недостаток" можно превратить в "достоинство" данного способа построения проекций 3ПГК-n, особенно при построении горизонтальных проекций 3ПГК-n. Как уже упоминалось ранее, не рекомендуется начинать построение горизонтальных проекций 3ПГК-n, пользуясь идеально правильной проекцией "исходной" правильной n-угольной пирамиды, - у вас будет на чертежах (особенно при n = четному числу) совмещение вершин, ребер, граней и даже кубов. Это нормально, правильно. Чаще всего это – визуальное совмещение.
Ребра – измерения
Поясняю, что я называю ребрами-измерениями. Итак, (см. рис. 1.1) в каждой 3ПГК-n автор определил две "исходные" правильные n-угольные пирамиды: верхнюю "исходную" пирамиду с вершиной +S, расположенную в первом "ярусе" между параллельными плоскостями РI и РII, и нижнюю "исходную" пирамиду с вершиной –S, расположенную в последнем, n- "ярусе", между параллельными плоскостями Рn и Рn+I.
Боковые ребра этих двух "исходных" пирамид назовем ребрами-измерениями. Если принять направления в пространстве n ребер-измерений, исходящих из вершины +S верхней пирамиды, положительно направленными ребрами-измерениями (+), то, соответственно, n ребер-измерений, исходящих из вершины –S нижней пирамиды, надо считать отрицательно направленными ребрами-измерениями (-). – Это с одной стороны.
А с другой стороны: ребра-измерения имеют свою векторную направленность относительно именно данной рассматриваемой вершины в 3ПГК-n.
Поясняю, как я это понимаю: любое ребро в 3ПГК-n соединяет две вершины 3ПГК-n; если для одной из этих двух вершин это ребро является положительным ребром-вектором, то для второй вершины (или относительно второй вершины) это же ребро является отрицательным ребром-вектором. Все в Мироздании относительно. Все познается в сравнении.
Поэтому, когда вы начертите горизонтальную проекцию "исходной" правильной n-угольной пирамиды с вершиной в точке +S, вы должны мысленно или на чертеже сразу же обозначить (начертить) противоположные ребра-измерения нижней "исходной" пирамиды с вершиной в точке –S.
Обратим особое внимание на следующее:
1) в 3ПГК-n, где n – четное число (т.е. n = 4, 6, 8, 10, ...), основания "исходных" пирамид (т.е. правильные n-угольники) геометрически зеркальны, то есть при строго вертикальном совмещении этих двух правильных n-угольников их вершины и ребра совместятся.
В этом случае горизонтальная проекция двух "исходных" пирамид (введем аббревиатуру: ГП 2ИП-n ) на чертеже (см. рис. 3.13) представлена в виде n ребер-измерений, но каждое из этих n ребер-измерений содержит в себе два ребра-измерения различных между собою по знаку;
2) в 3ПГК-n, где n – нечетное число (т.е. n = 3, 5, 7, 9, ...), при строго вертикальном совмещении оснований верхней и нижней "исходных" пирамид - и вершины, и, соответственно, ребра этих правильных n-угольников геометрически не совмещены. В этом случае горизонтальная проекция двух "исходных" пирамид (ГП2ИП-n) на чертеже представлена в виде 2n ребер-измерений, где n ребер-измерений являются положительными векторами-измерениями и, соответственно, другие n ребер-измерений являются отрицательными векторами измерениями.
Вот поэтому в первом случае, когда n равно четному числу (n = 4, 6, 8, 10, ...), в самих гиперкубах-n (ГК-n) и в их 3ПГК-n образуются реальные геометрически совмещенные вершины, и в любой проекции, в любом ракурсе, на всех чертежах именно эти вершины будут всегда совмещены.
Во втором случае, когда n равно нечетному числу (n = 3, 5, 7, 9, ...), в самих гиперкубах-n (ГК-n) и в их 3ПГК-n нет ни одной геометрически совмещенной вершины, в горизонтальной проекции совмещены только две вершины: +S и –S, но это – визуальное совмещение, необходимое при построении именно этой проекции. В зависимости от выбранного ракурса изображения можно достичь на чертежах много визуально совмещенных вершин, даже ребер, граней и кубов, но это будет лишь визуальное совмещение.
Полигон измерений
Выражение, понятие "ребро-измерение" подразумевает, что это векторная величина. Следовательно, из этих векторных величин ("ребер-измерений") можно составить полигон измерений.
Полигон измерений, составленный из n "ребер-измерений" в горизонтальных проекциях "исходных" правильных n-угольных пирамид всегда будет замкнутым ("обнулеванным").
Понятие "горизонтальная проекция 3ПГК-n" предусматривает совмещение на чертеже вершин +S и –S "исходных" пирамид.
Если же полигон измерений не будет замкнутым, "обнулеванным", т.е. если между началом и концом полигона измерения будет «какое-то» расстояние, то это означает, что на это же "какое-то" расстояние будут разъединены вершины +S и –S, следовательно, это уже не будет именно горизонтальная проекция 3ПГК-n, а получится просто "другой ракурс" 3ПГК-n.
Абрис
Абрис – это контур, очертание внешней границы любой начерченной проекции 3ПГК-n.
Составными частями абриса для данного чертежа проекции 3ПГК-n являются 2n ребер-измерений верхней и нижней «исходных» пирамид, причем проекции n боковых ребер верхней «исходной» пирамиды с вершиной +S считаются положительно направленными ребрами, а проекции n боковых ребер нижней "исходной" пирамиды с вершиной –S считаются отрицательно направленными ребрами.
Последовательность расположения этих ребер-измерений в абрисе строго обусловлена.
На рис. 3.13 представлен метод построения абриса горизонтальных проекций 3ПГК-n "по клеткам":
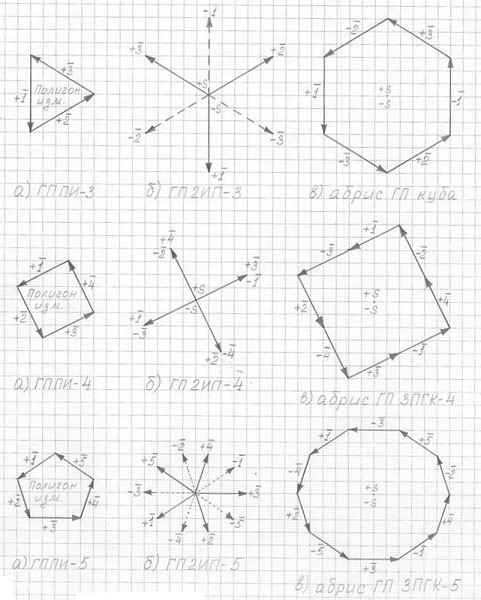
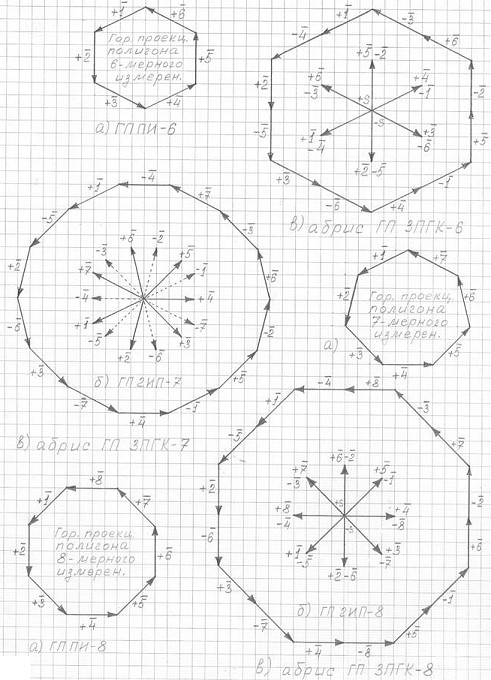
Рис. 3.13
Горизонтальные проекции: а) полигона n-мерных измерений (ГП ПИ-n)
б) двух исходных пирамид (ГП 2ИП-n)
в) абрис горизонтальной проекции 3ПГК-n
(а) строится горизонтальная проекция полигона n-мерного измерения (в идеале это правильный n-угольник). Пронумеровать "ребра-измерения". (Введем аббревиатуру: ГП ПИ-n);
(б) используя "ребра-измерения", образующие полигон измерений, чертим горизонтальную проекцию двух "исходных" правильных n-угольных пирамид 3ПГК-n. (Введем аббревиатуру: ГП 2ИП-n).
В этой проекции вершины пирамид +S и –S совмещены, при этом: n "ребер-измерений", исходящих из вершины +S, будут положительно направленными, а другие n "ребер-измерений", исходящих из вершины –S, будут отрицательно направленными.
Обратите внимание: в ГП 2ИП-n положительно направленные "ребра-измерения" и отрицательно направленные "ребра-измерения" всегда лежат на одной прямой, но:
- в ГП 2ИП-n, где n – нечетное число (т.е. n = 3, 5, 7, 9, ...), положительно и отрицательно направленные "ребра-измерения" лежат на одной прямой, но отдельно от соседних "ребер-измерений";
- в ГП 2ИП-n, где n – четное число (т.е. n = 4, 6, 8, 10, ...), положительно и отрицательно направленные "ребра-измерения" лежат тоже на одной прямой, но ввиду "зеркальности" "исходных" пирамид – эти "ребра-измерения" еще и сдвоены, т.е. совмещены;
(в) создается абрис горизонтальной проекции 3ПГК-n из "ребер-измерений" ГП 2ИП-n, при этом:
- при n, равном нечетному числу (т.е. n = 3, 5, 7, 9, ...), абрис выглядит в виде 2n-угольника (в идеале – правильного);
- при n, равном четному числу (т.е. n = 4, 6, 8, 10, 12, ...), абрис выглядит в виде n-угольника, но каждая сторона этого n-угольника состоит из двух разнознаковых "ребер-измерений".
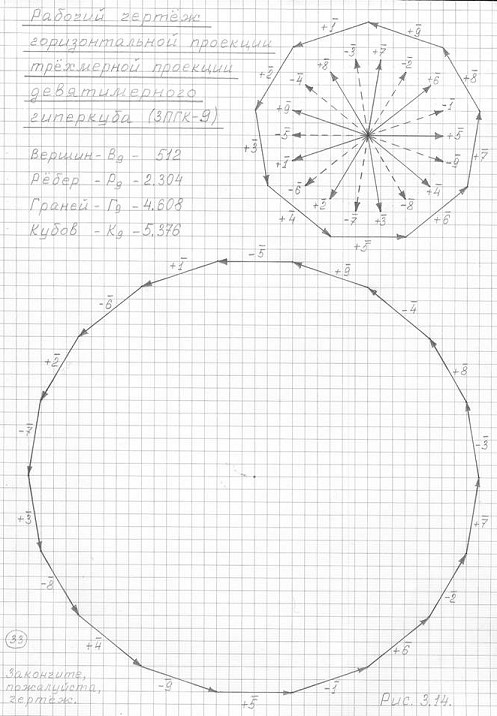
Рис. 3.14
Метод построения горизонтальной проекции 3ПГК-n с помощью абриса представлен на рис. 3.15 на примере построения трехмерной проекции пятимерного гиперкуба (3ПГК-5).
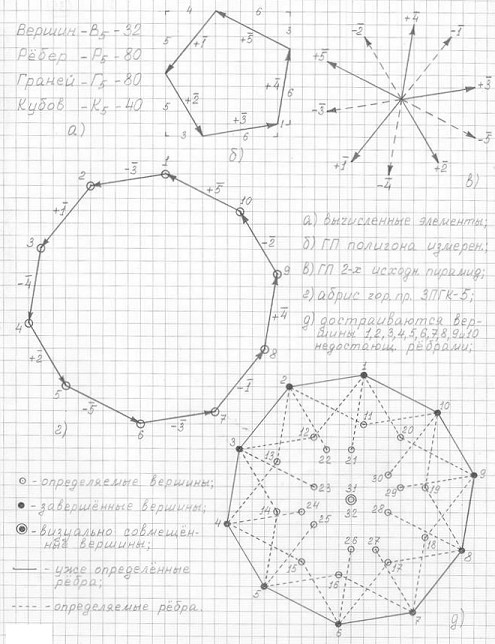
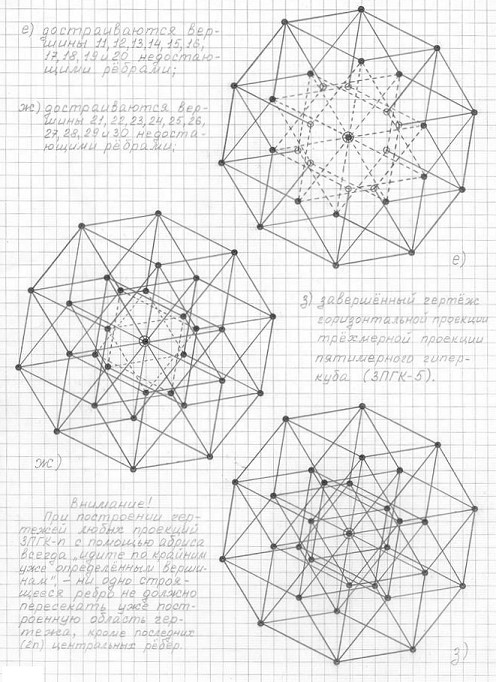
Рис. 3.15
Этапы построения горизонтальной проекции 3ПГК-5
Создание абриса с помощью начерченных "исходных" правильных n-угольных пирамид в любом ракурсе, в любой другой проекции автор несколько упростил (см. рисунки 3.16, 3.18, 3.19, 3.20, 3.23, 3.26, 3.27, 3.28, 3.29, 3.30 и др.), т.е. достаточно начертить "исходную" правильную n-угольную пирамиду в любом ракурсе, в любой проекции, пронумеровать n ее боковых ребер в определенном направлении (слева-направо или справа-налево) и, начиная с вершины +S, в том же выбранном направлении последовательно, ребро за ребром, соединить все n ребер, - поставить точку -S; теперь от вершины –S в той же последовательности ребро за ребром соединить все n ребер, - абрис в виде замкнутого круга готов.
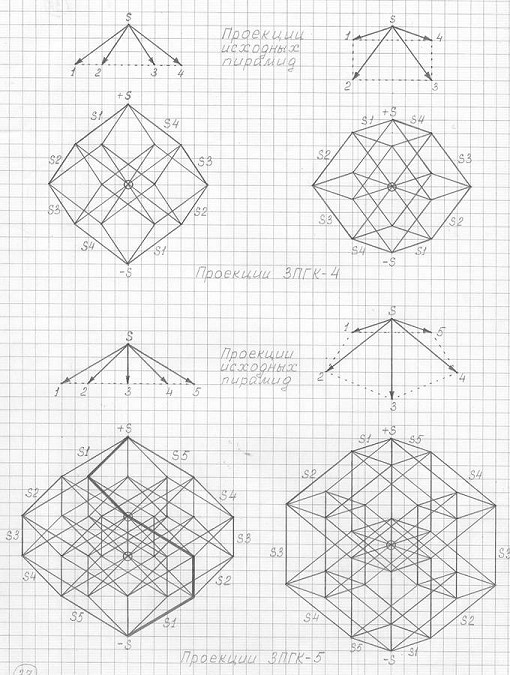
Рис. 3.16
В случаях, когда проекция "исходной" пирамиды содержит совмещенные на чертеже боковые ребра, то именно эти ребра и в абрисе, и в данной проекции 3ПГК-n всегда откладываются дважды (см. рисунки 3.19, 3.20, 3.28, 3.29, 3.35 ).
Метод построения (черчения) по созданному абрису всех 3ПГК-n представлен на рис. 3.15.
На рис. 3.17 (б) представлен идеальный чертеж горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5).
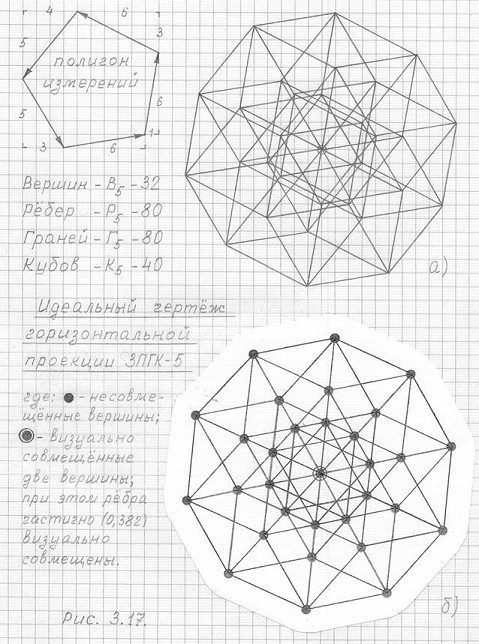
Рис. 3.17
Чертежи горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5)
Думаю, вы согласитесь, что осмыслить идеальный чертеж 3ПГК-5 намного легче с помощью вспомогательного чертежа 3ПГК-5 (рис. 3.17, а), построенного "по клеткам", где все вершины, ребра, грани индивидуально выражены. Вот это и есть достоинство строения (черчения) всех проекций 3ПГК-n "по клеткам".
Уважаемые геометры! У вас есть компьютеры. Прежде, чем оценивать работу автора, пожалуйста, с помощью компьютерной графики достройте чертеж ГП 3ПГК-9 на рис. 3.14 – это очень интересно. Чертить этот чертеж на бумаге карандашом, как это делает автор, очень трудно – от обилия линий (2304 ребра) не выдерживает, вспучивается бумага (см. рис. 3.39 и 3.41) и подводит зрение. А на компьютере можете каждую деталь чертежа увеличить в масштабе.
Итак, чертежи трехмерной проекции четырехмерного гиперкуба (3ПГК-4) уже представлены в этой работе во всех проекциях и интересных ракурсах.
Предлагаю вашему вниманию чертежи трехмерной проекции пятимерного гиперкуба (3ПГК-5) в трех проекциях: горизонтальной (H'), фронтальной (V') и профильной (W'), построенных с помощью соответствующих трех проекций (H, V и W) "исходной" правильной пятиугольной пирамиды SADCDE, горизонтальной проекции полигона измерений и созданных соответствующих данным проекциям абрисов (см. рис. 3.18, 3.19 и 3.20).
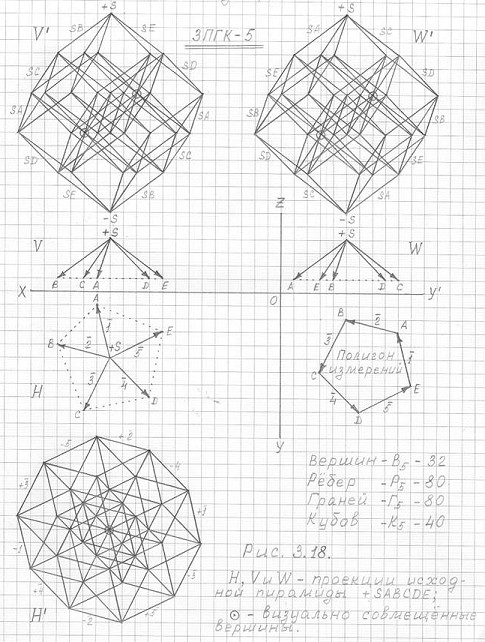
Рис. 3.18
Чертежи горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5) в трехпроекциях (H', V' и W'), построенные с помощью исходной пирамиды +SABCDE и полигона измерений.
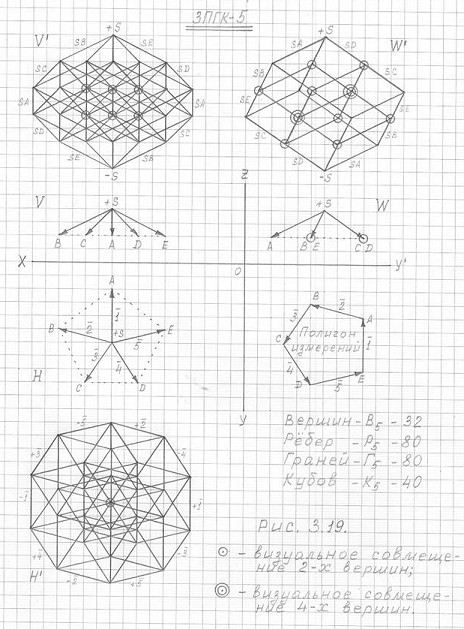
Рис. 3.19
Чертежи горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5) в трехпроекциях (H', V' и W'), построенные с помощью исходной пирамиды +SABCDE в трех соответствующих проекциях (H, V и W) и полигона измерений.
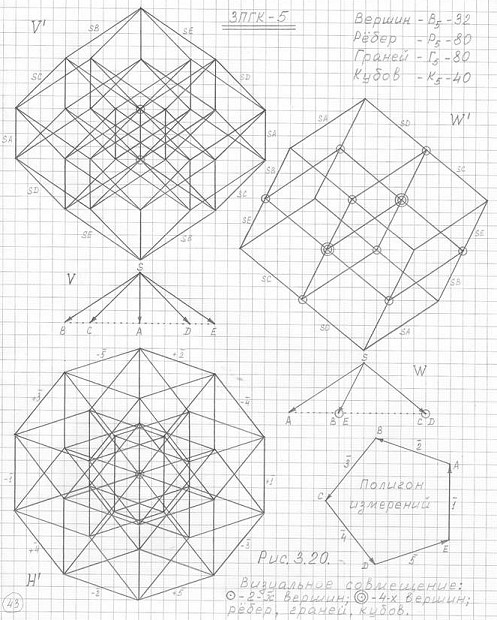
Рис. 3.20
Чертежи горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5) в трехпроекциях (H', V' и W'), построенные с помощью исходной пирамиды +SABCDE и полигона измерений.
На рис. 3.21 представлены чертежи 3ПГК-5 во фронтальной (или профильной) проекции, причем в одном чертеже 3ПГК-5 есть визуальное совмещение двух ребер, а следовательно, и вершин; во втором случае – чертеж 3ПГК-5 представлен без совмещения ребер и вершин; и первый и второй ракурсы изображения вполне реальны.
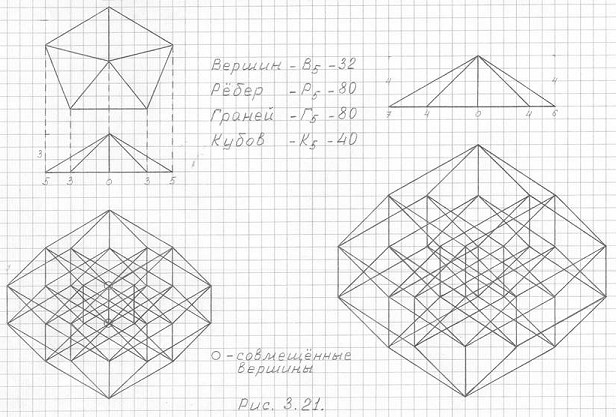
Рис. 3.21
Чертежи горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5) в фронтальной (или профильной) проекции.
Рис. 3.22 укрепит вашу уверенность в возможности построения 3ПГК-n в разных ракурсах.
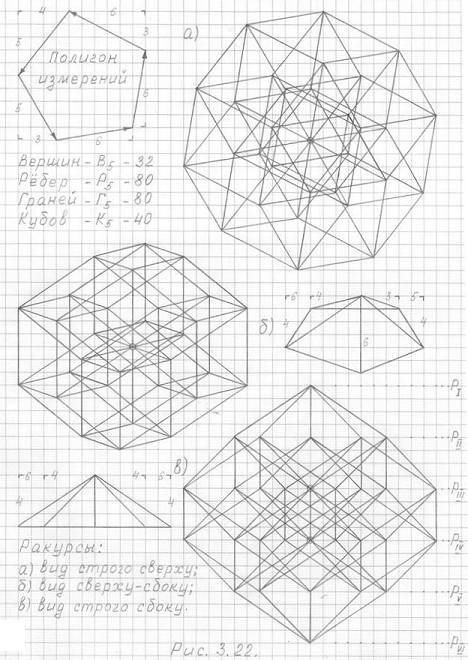
Рис. 3.22
Чертежи горизонтальной проекции трехмерной проекции пятимерного гиперкуба (3ПГК-5) в разных ракурсах
Чертить на одной странице 3ПГК-n, где n больше пяти (т.е. 3ПГК-6, 3ПГК-7 и т.д.) в трех проекциях (горизонтальной, фронтальной и профильной) трудно из-за тесноты площади страницы, поэтому различные 3ПГК-n в различных ракурсах и проекциях предлагаются вам избирательно и обзорно.
Надеюсь, по полигону измерений или по виду проекции "исходной" пирамиды, начерченных к каждому чертежу 3ПГК-n, вам не трудно будет сориентироваться в проекциях, методах и способах построения самих чертежей 3ПГК-n.
В этой работе я хочу убедить вас, что с помощью изображения "исходной" правильной n-угольной пирамиды в любой проекции, в любом ракурсе (что не составит труда для любого геометра) можно начертить соответствующий чертеж 3ПГК-n в той же проекции и в том же ракурсе – что и является универсальным методом построения (черчения) 3ПГК-n.
По любой проекции "исходной" правильной n-угольной пирамиды стройте абрис. Абрис уже содержит всю необходимую информацию для построения (черчения) 3ПГК-n в выбранных проекциях и ракурсах.
Продолжим обзор построения (черчения) 3ПГК-n в различных ракурсах, разумеется, переходя к более высоким измерениям.
Среди множества созданных чертежей 3ПГК-n найдем чертежи наиболее интересных ракурсов.
Предлагаю вашему вниманию рис. 3.23 и рис.3.24. Чертежи рис. 3.23 радуют меня своей элегантностью, совершенством линий – воистину, это - Геометрия Высших Миров.
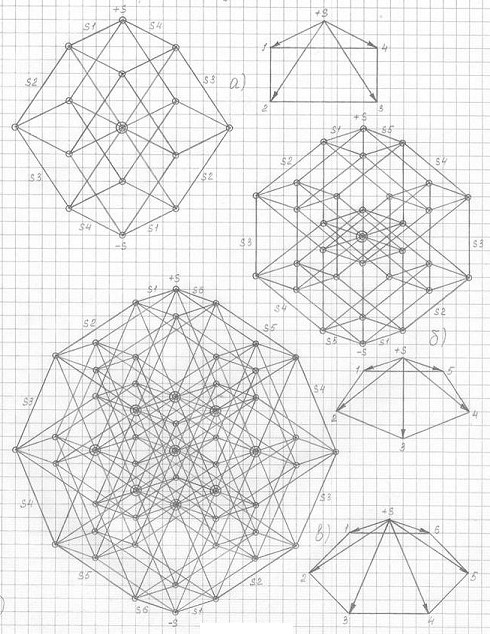
Рис. 3.23
Чертежи трехмерных проекций:
а) четырехмерного гиперкуба 3ПГК-4
б) пятимерного гиперкуба 3ПГК-5
в) шестимерного гиперкуба 3ПГК-6
Ракурс: вид сбоку-сверху
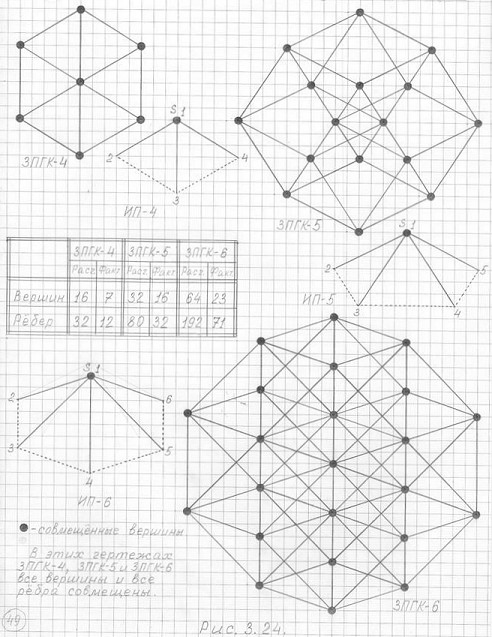
Рис. 3.24
Самый оригинальный ракурс черчения 3ПГК-n параллельный одному ребру исходной пирамиды.
Ракурс же чертежей рис. 3.24 оригинален тем, что чертежи 3ПГК-4 и 3ПГК-5 содержат минимально возможные количества вершин и ребер, а чертеж 3ПГК-6 по минимальности количества вершин и ребер уступает только чертежу своей горизонтальной проекции.
Чертеж горизонтальной проекции 3ПГК-6 представлен на рис. 3.25 (б). Чертеж очень прост. Но что стоит за этой простотой? Чтобы понять это, надо (помните? – я это уже упоминалось) слегка, чуть-чуть изменить ракурс [см. чертеж (а)], и вот этот чертеж (а) покажет что скрывается за этой величественной простотой. Какое колоссальное визуальное совмещение вершин, ребер, граней, кубов!
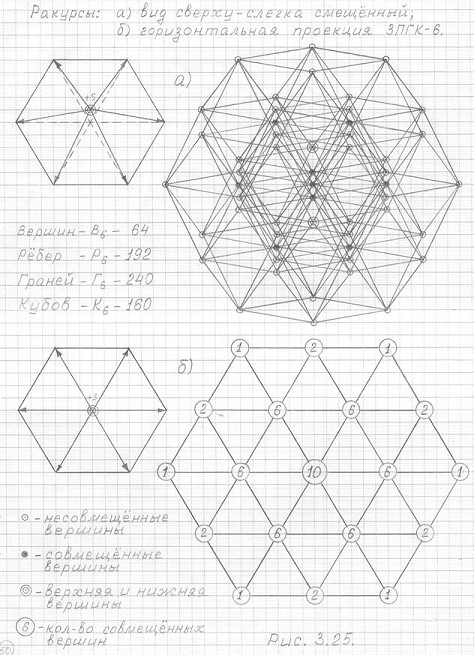
Рис. 3.25
Чертежи трехмерной проекции шестимерного гиперкуба 3ПГК-6
Ракурсы:
а) вид сверху слегка смещенный
б) горизонтальная проекция 3ПГК-6
Повторяю: горизонтальная проекция у всех 3ПГК-n только одна. При построении (черчении) горизонтальных проекций 3ПГК-n следует помнить, что:
1) при n равном четному числу (т.е. n = 4, 6, 8, 10, 12, ...) горизонтальная проекция 3ПГК-n будет содержать кроме собственных геометрически обусловленных совмещенных вершин еще очень значительное визуальное совмещение вершин, ребер, граней, кубов (см. рис. 3.25, 3.37, 3.40, 3.42);
2) при n равном нечетному числу (т.е. n = 5, 7, 9, 11, ...) горизонтальная проекция 3ПГК-n имеет только две совмещенные вершины: +S и –S, но это – визуальное совмещение, необходимое при построении именно этой проекции; однако в этих горизонтальных проекциях 3ПГК-n будет очень большое число частичных совмещений ребер на чертеже, т.е. одно ребро визуально совмещается с другим ребром только частью своей длины (см. рис. 3.17, 3.32).
Предлагаю вашему вниманию 4 чертежа трехмерной проекции шестимерного гиперкуба (3ПГК-6) в разных ракурсах ее фронтальных проекций (см. рис. 3.26, 3.27, 3.28 и 3.29). Обратите внимание: в этих чертежах взяты основные ракурсы фронтальной проекции "исходной" пирамиды – и как разительно при этом меняется сама фронтальная проекция 3ПГК-6!
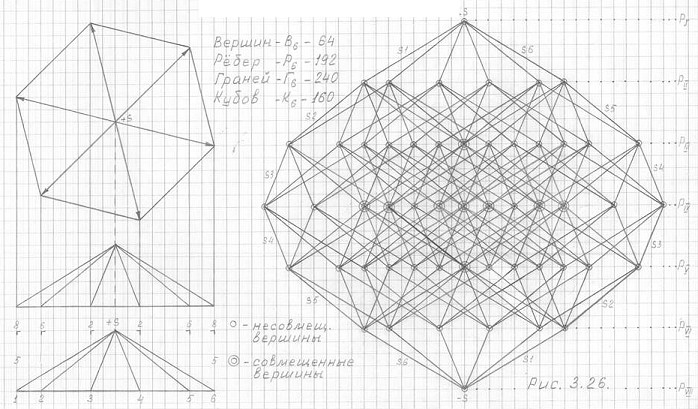
Рис. 3.26
Чертеж трехмерной проекции шестимерного гиперкуба 3ПГК-6.
Фронтальная проекция.
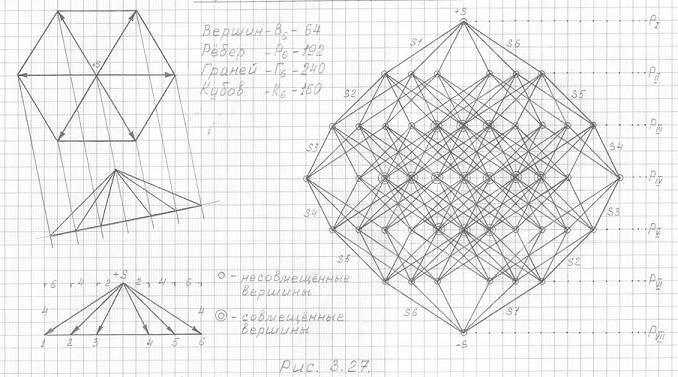
Рис. 3.27
Чертеж трехмерной проекции шестимерного гиперкуба 3ПГК-6.
Фронтальная проекция.
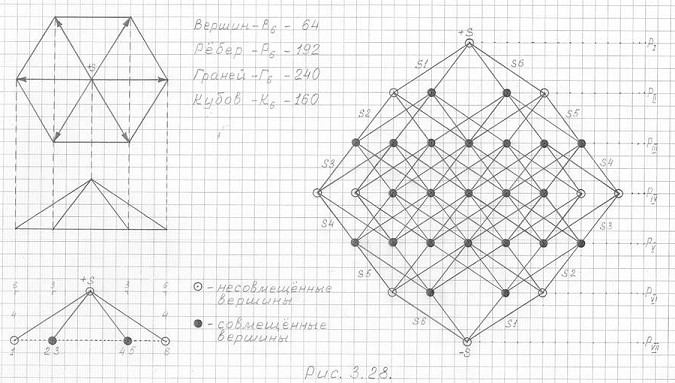
Рис. 3.28
Чертеж трехмерной проекции шестимерного гиперкуба 3ПГК-6.
Фронтальная проекция.
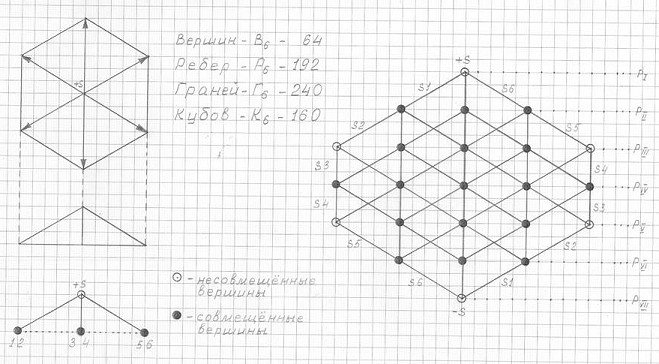
Рис. 3.29
Чертеж трехмерной проекции шестимерного гиперкуба 3ПГК-6.
Фронтальная проекция.
А вот очень интересный ракурс изображения 3ПГК-6 (см. рис. 3.30). Этот чертеж дает очень наглядное представление о расположении граней и кубов в 3ПГК-6, а также о расположении геометрически обусловленных совмещенных вершин.
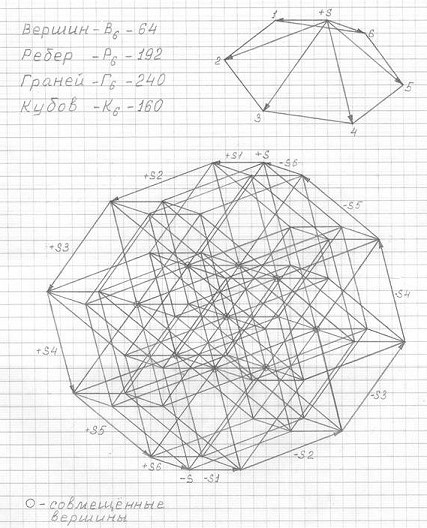
Рис. 3.30
Чертеж трехмерной проекции шестимерного гиперкуба 3ПГК-6.
Ракурс: вид сбоку-сверху.
Считаю, что и 3ПГК-4, и 3ПГК-5, и 3ПГК-6 достаточно представлены в разных своих ракурсах и проекциях.
Переходим к чертежам трехмерной проекции семимерного гиперкуба (3ПГК-7).
Горизонтальная проекция 3ПГК-7 представлена в виде рабочего чертежа (см. рис. 3.31), построенного "по клеткам", и так называемого мною "идеального" чертежа (см. рис. 3.32). Правильные многоугольники для построения "идеальных" чертежей можно построить с помощью линейки, циркуля и транспортира.
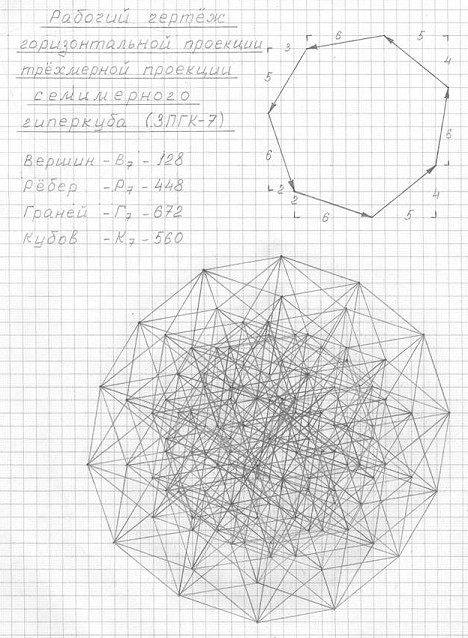
Рис. 3.31
Рабочий чертеж горизонтальной проекции трехмерной проекции семимерного гиперкуба (3ПГК-7)
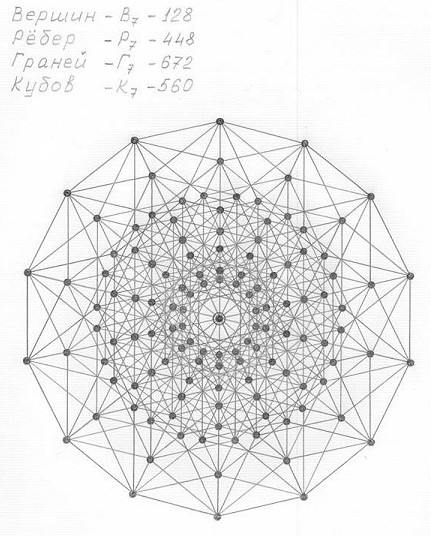
Рис. 3.32
Чертеж трехмерной проекции семимерного гиперкуба (3ПГК-7)
Горизонтальная проекция
Рабочий чертеж горизонтальной проекции 3ПГК-n дает возможность проследить не только расположение каждого ребра в отдельности, но и выявить схему построения ее "идеальной" проекции.
ФРабочие чертежи фронтальных проекций трёхмерных проекций семимерных гиперкубов (3ПГК-7) представлены на рис. 3.33, 3.34 и 3.35.
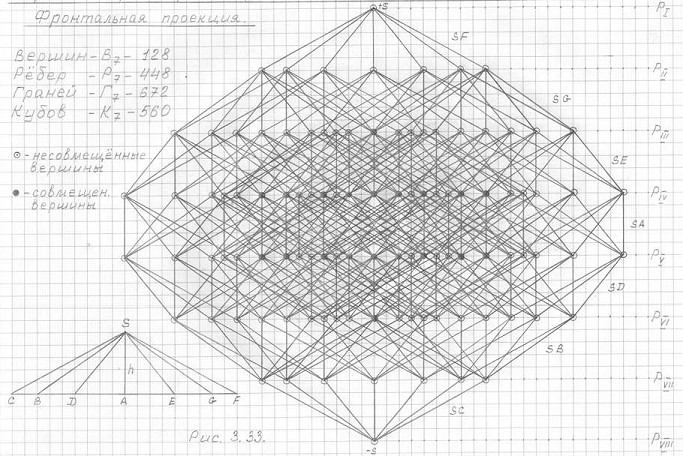
Рис. 3.33
Чертеж трехмерной проекции семимерного гиперкуба (3ПГК-7)
Фронтальная проекция
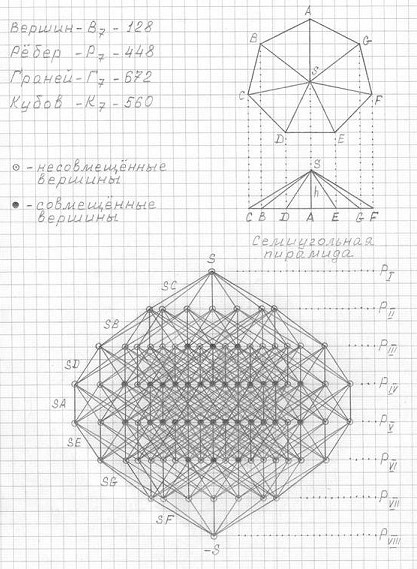
Рис. 3.34
Чертеж трехмерной проекции семимерного гиперкуба (3ПГК-7)
Фронтальная (или профильная) проекция
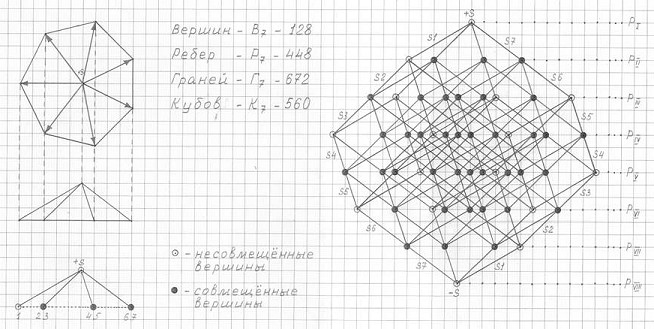
Рис. 3.35
Чертеж трехмерной проекции семимерного гиперкуба (3ПГК-7)
Фронтальная проекция
А на рис. 3.36 трёхмерная проекция семимерного гиперкуба (3ПГК-7) изображена в "самом оригинальном ракурсе": все вершины, ребра, грани – визуально совмещены! Чертёж изумительной красоты! Я люблю эти чертежи. Заметили? В основном, все они приводят меня в восторг своей грацией, элегантностью, совершенством. Воистину, это – Геометрия Высших Миров!
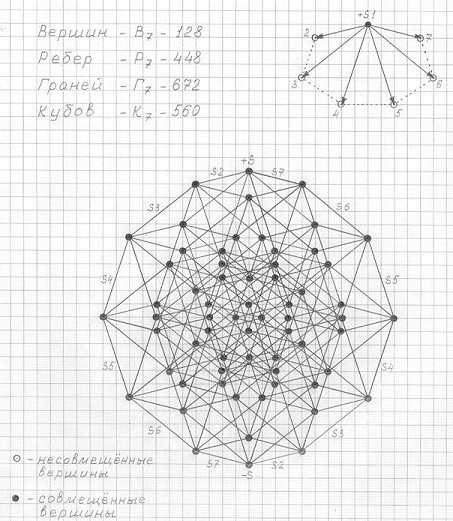
Рис. 3.36
Чертеж трехмерной проекции семимерного гиперкуба (3ПГК-7)
Оригинальный ракурс: визуальное совмещение вершины (+S) исходной пирамиды с вершиной (1) основания этой пирамиды.
Трехмерная проекция восьмимерного гиперкуба (3ПГК-8) представлена чертежами ее горизонтальной
проекции (рис. 3.37) и фронтальной проекцией (рис. 3.38).
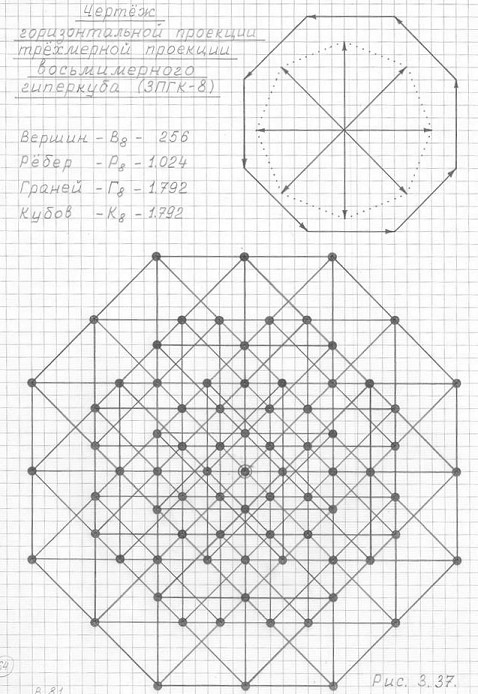
Рис. 3.37
Чертеж горизонтальной проекции трехмерной проекции восьмимерного гиперкуба (3ПГК-8)
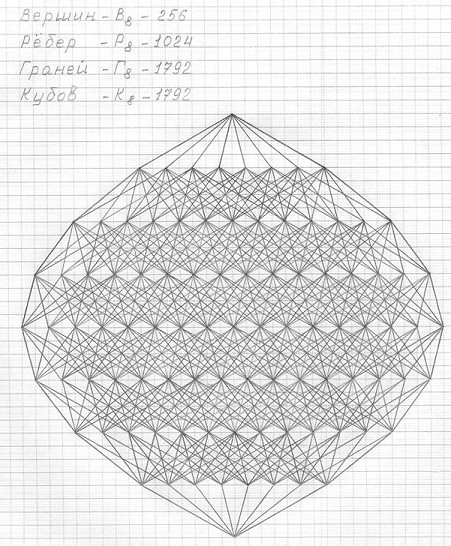
Рис. 3.38
Чертеж трехмерной проекции восьмимерного гиперкуба (3ПГК-8)
Фронтальная проекция
Трехмерная проекция десятимерного гиперкуба (3ПГК-10) представлена чертежом ее горизонтальной проекции (рис. 3.40) и рабочим чертежом (рис. 3.39) для построения этой проекции.
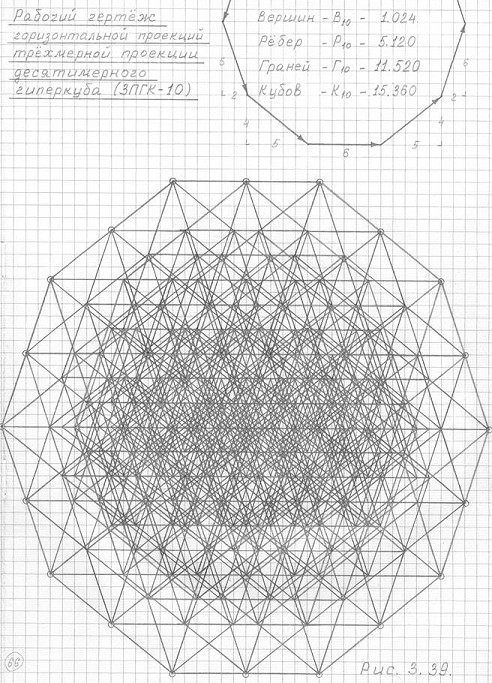
Рис. 3.39
Рабочий чертеж горизонтальной проекции трехмерной проекции десятимерного гиперкуба (3ПГК-10)
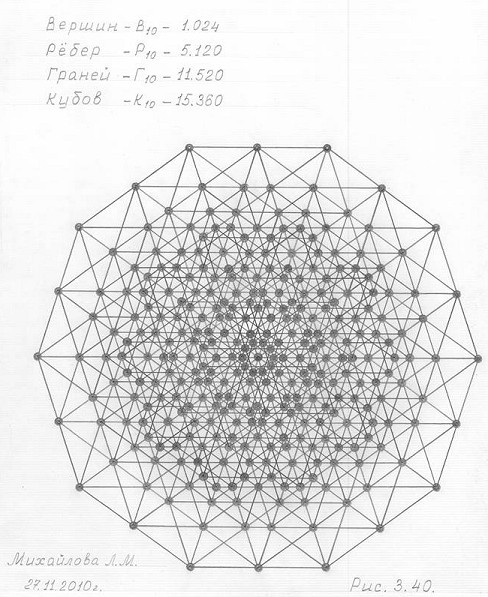
Рис. 3.40
Чертеж горизонтальной проекции трехмерной проекции десятимерного гиперкуба (3ПГК-10)
Трехмерная проекция двенадцатимерного гиперкуба (3ПГК-12) представлена чертежом ее горизонтальной проекции (3.42) и рабочим чертежом (рис. 3.41) для построения этой проекции.
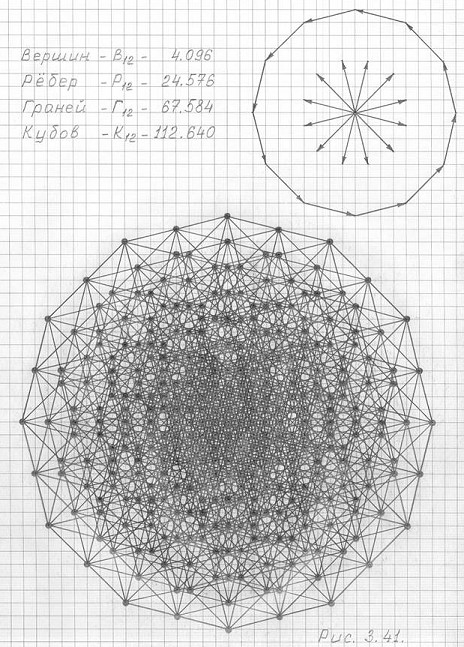
Рис. 3.41
Рабочий чертеж горизонтальной проекции трехмерной проекции двенадцатимерного гиперкуба (3ПГК-12)
Трехмерная проекция двенадцатимерного гиперкуба (3ПГК-12) представлена идеальным чертежом ее горизонтальной проекции (3.42) и рабочим чертежом (рис. 3.41) для построения этой проекции.
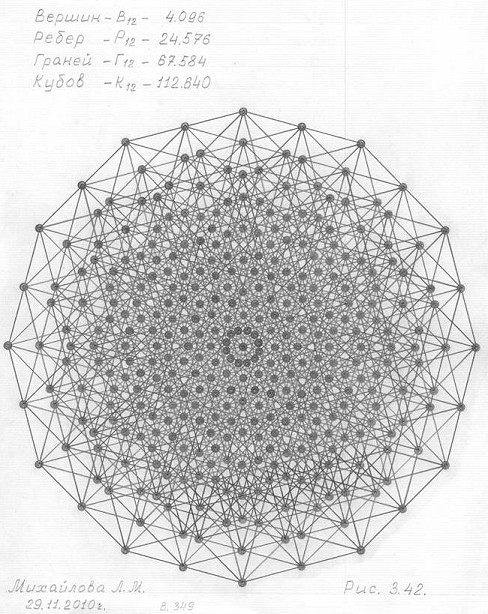
Рис. 3.42
Чертеж горизонтальной проекции трехмерной проекции двенадцатимерного гиперкуба (3ПГК-12)
Забавы ради предлагаю вам мою версию четырехмерного кубоида (см. рис. 3.43). n-мерные кубоиды существуют только в двумерном пространстве (рис. 3.43).
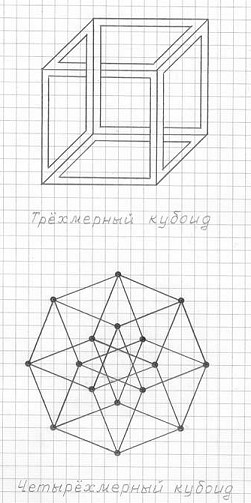
Рис. 3.43
Кубоиды
Уважаемые геометры, надеюсь, вы согласитесь, что с помощью предложенного в данной главе "Универсального метода построения любых проекций 3ПГК-n" можно чертить все 3ПГК-n в любых проекциях и ракурсах, а с помощью компьютерной графики, надеюсь, чертить будет намного легче.
Более того, из трубочек и лески вполне реально можно создавать все модели 3ПГК-n.
