Обманутый глаз
6. Истоки и история


Во время поисков невозможных фигур, созданных до 1934 года, когда Оскар Реутерсвард начал осознанно заниматься данным предметом, выяснилось, что такие объекты, в основном, можно найти в изобразительном искусстве до появления работ в классической перспективе. Они были созданы бессознательно, но всегда с определенной целью.
Наиболее старый из известных на сегодняшний день примеров найден среди миниатюр перикопы Генриха II, собранной до 1025 года и хранящийся сегодня в Bayerische Staatsbibliothek в Мюнхене. "Мадонна с ребенком", представленная выше слева, взятая из "Поклонения волхвов" (Adoration of the Magi) содержит центральную колонну, которая должна оканчиваться на переднем плане. Однако, если она была бы так нарисована, то она загородила бы фигуру Богородицы. Вместо этого, верхняя часть колонны изображена на переднем плане, а нижняя – на заднем, формируя невозможный объект из категории "множественная плоскость".
Другой важный пример был найден на фреске XV века, изображающей Благовещение в храме Grote Kerk в г. Бреда (Голландия) (сверху справа). Историк J. Kalf первым обнаружил, что с центральной колонной что-то не в порядке. Данный невозможный объект схож с миниатюрой из перикопы как сюжетом произведения, так и причиной, по которой колонны изображены подобным образом.
Сознательное создание невозможного объекта относительно новое явление. В 1934 году Оскар Реутерсвард впервые нарисовал невозможный трибар. В 1958 году Эшер изобрел невозможный куб и включил его в свою литографию "Бельведер". Статья Пенроуза и сына о невозможном трибаре и бесконечной лестнице появилась в том же году. Эшер использовал эти две фигуры в качестве моделей для своих работ "Водопад" (1961) и "Восхождение и спуск" (1960). У нас есть достаточно четкое представление о последних событиях, полученных напрямую из уст автора.
Однако, во второй половине данной главы мы увидим, что невозможные объекты, осознанно или неосознанно, существуют гораздо больший промежутой времени. Самые ранние примеры датируются XI веком.
Оскар Реутерсвард: изобретатель невозможных фигур
Примечательно, что Реутерсвард нарисовал свой первый невозможный объект совершенно случайно. Тем не менее, он понял, что фигура обладает особенными, ранее неиспользовавшимися, свойствами. Он рассказывает свою историю в одном из писем: "В старших классах я изучал латынь и философию вместо математики и биологии. На уроках латыни, пока учитель рассказывал поучительные истории о римлянах, практически каждый ученик рисовал эскизы на полях грамматики по латыни. Я пытался рисовать звезды с четырьмя, пятью, шестью, семью или даже восемью лучами настолько правильными, насколько это было возможно. Однажды, когда я обводил шестиконечную звезду кругом из кубов, я обнаружил, что кубы сформировали странное сочетание. Движимый необъяснимым импульсом, я добавил три куба, чтобы получился треугольник. Я был достаточно догадлив, чтобы понять, что нарисовал парадоксальную фигуру. После урока я показал рисунок моему другу и однокласснику Яну Корнеллу (Jan Cornell), который был одержим математикой. Он воскликнул: "Я не видел ничего подобного раньше! Ты должен посмотреть в математической энциклопедии, что там сказано про эти невероятные геометрические объекты!" Я поспешил в Стокгольмскую городскую библиотеку, где я долгое время тщетно искал примеры объектов с похожими свойствами.
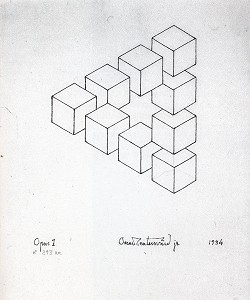
Рисунок 1. Оскар Реутерсвард, "Opus 1 n° 293 aa", 1934
Следующие несколько лет я время от времени играл с "кубами в парадоксальных сочетаниях", создав бесконечную лестницу и фигуры наподобие вилки дьявола. Кстати, моя вилка немного отличается от той, которая впоследствии была опубликована Шустером (Schuster), так как она была получена из невозможных извилин (рисунок 29). В то время я на называл свои фигуры "иллюзорными телами".
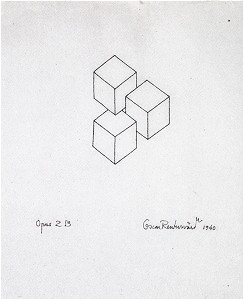
Рисунок 2. Оскар Реутерсвард, "Opus 2B", 1940
В 1958 году тот же Ян Корнелл (теперь уже известный издатель) дал мне прочитать статью, в которой Пенроузы описали несколько невозможных объектов. Только после этого я понял, что я открыл в детстве. До той поры я нарисовал порядка сотни невозможных объектов, и статья Пенроузов вдохновила меня на исследования в данной области. На сегодняшний день (на 1986 год) я нарисовал примерно 2500 невозможных объектов."
Способ, которым Реутерсвард достиг бесконечной лестницы, также проливает свет на метод, при котором его невозможные объекты выстаиваются во взаимосвязанные серии: "За несколько дней до моего путешествия из Стокгольма в Париж (в мае 1950 года) я прослушал по радио интересную программу о методе сочинения Моцартом своих произведений. Его манера работы описывается термином 'творческий автоматизм'. Каждое новое произведение, которое он писал, порождало идею для нового произведения и т.д. Я почувствовал, что аналогично описывается и мой путь, которым я разрабатывал невозможные объекты. Я решил во время поездки отмечать время и место начала последовательности невозможных объектов, созданные таким 'бессознательным', автоматическим способом. Это был трудный, но в то же время интересный и плодотворный, эксперимент, который позволил проследить разработку все более сложных фигур шаг за шагом. Я нарисовал четырнадцать рисунков за время 40-часового путешествия. Это странно, но в то время я так и не понял, что получил фигуру, которая фактически была непрерывным лестничным пролетом. Лишь несколько лет спустя я сознательно стал затрагивать данную тему." (рисунки 3-5).
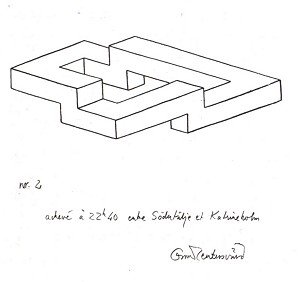
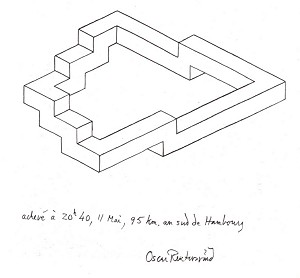
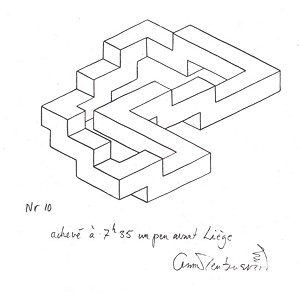
Рисунок 3-5. Оскар Реутерсвард, наброскиn из путешествия, 1950
Реутерсвард писал об Эшере: "Я очень, очень большой поклонник Эшера. Впервые его невозможные объекты я увидел в 1961 году, когда Ян Корнелл прислал мне репродукцию его картины "Восхождение и спуск". Я был очень впечатлен картиной, но не очень сильно нерегулярностью самой лестницы (2x15 + 2x9).
В 1962 году Корнелл прислал мне репродукцию "Водопада" Эшера, замечательную композицию, в которой я восторгаюсь трактовкой Эшером темы трибаров. В 1963 и 1964 году я написал Эшеру два письма, в которых я описал свое восхищение его работами. Но не получил никакого ответа. Я отправил ему выдержки из статей о его работах в шведских изданиях, но опять не получил ответа."

Рисунок 6. Стокгольм 1934г. Оскар Реутерсвард (справа) и Ян Корнелл (второй слева)

Рисунок 7. Оскар Реутерсвард, 1950
Рисование чего-то по-настоящему невозможного
На Эшеровском Конгрессе в 1985 году в Риме я разговаривал с Роджером Пенроузом о роли, которую он и его отец сыграли в открытии невозможного трибара и бесконечной лестницы. Кажется, он был очень вдохновлен работами Эшера, хотя в то время Эшер еще не нарисовал своих картин с невозможными объектами, и даже не подозревал об их существовании. Пенроуз пытался изобразить по-настоящему невозможный объект. Вот его слова: "Интерес к невозможным фигурами у меня возник в 1954 году, когда я, будучи студентом, посетил Международный Конгресс Математиков в Амстердаме. Я знал одного из докладчиков, и сообщил мне, что меня могла бы заинтересовать выставка работ голландского художника М.К. Эшера, которая специально была организована там одновременно с конгрессом. Я сходил, и я помню, что был ошеломлен его работами, которые увидел впервые в жизни.

Рисунок 8. Роджер Пенроуз, Рим, 1985 г. (фото Бруно Эрнста)
На обратном пути в Англию я решил нарисовать что-то "невозможное" самостоятельно. Я экспериментировал с различными комбинациями брусков, лежащий спереди и позади друг друга, и, в конце концов, пришел к невозможному треугольнику (впоследствии ставшему известным как невозможный трибар), который, как мне казалось, представлял невозможность в чистом виде.
Хотя на выставке было представлено множество экстраординарных работ Эшера, среди них не было ничего из того, что мы сегодня называем невозможными объектами. Я показал отцу получившийся ранее треугольник при первой возможности. Он немедленно сделал наброски нескольких вариантов фигур, придя, таким образом, к изображению невозможного лестничного пролета, постоянно ведущего вверх (или вниз). Мы хотели опубликовать наши открытия, но не знали где, так как было непонятно, в какую область науки попадает данная тема. Случилось так, что мой отец был знаком с редактором Британского Журнала Психологии, и он мог бы попросить о возможности напечатать нашу статью. Мы решили, что тема имеет отношение к психологии, и отправили ему нашу короткую рукопись. Статья была напечатана в 1958 году. Мы отправили один экземпляр Эшеру в дань уважения. В то время никто из нас не знал о более ранних работах Оскара Реутерсварда, о которых мне стало известно только 1984 году."
Знаменитая статья Перноузов полностью напечатана ниже.
"Невозможные объекты: Особый вид зрительной иллюзии"
Л.С. и Р. Пенроузы, Университетский колледж (Лондон) и Колледж Бедфорда (Лондон). (Рукопись получена 30 ноября 1956 года)
"Двухмерные рисунки могут передавать впечатление, как от трехмерных объектов. При определенных обстоятельствах этот факт может использоваться для создания противоречивых интерпретаций. Многочисленные идеи из данной области эксплуатируются М.К. Эшером (1954). Данная статья описывает особый вид фигур. Каждая отдельная часть фигуры воспринимается как представление объекта, расположенного в трехмерном пространстве, однако, из-за неверного соединения отдельных частей вся фигура приводит к созданию иллюзорного эффекта невозможной структуры. Простейший пример показан на рисунке 9. Это изображение в перспективе, каждая часть которого представляется трехмерную прямоугольную структуру. Однако, линии на рисунке соединены таком образом, что получается невозможность. Так как глаз следует по линиям фигуры, ему приходится неожиданно менять интерпретацию определения расстояния от наблюдателя до объекта. Более сложная структура (не в перспективе) представлена на рисунке 10. Так как этот объект анализируется следованием взглядом по его поверхностям, изменения интерпретации происходят очень часто.
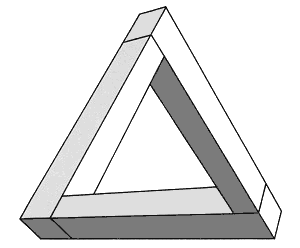
Рисунок 9.
Рисунок 10.
Другой способ представленная того же самого типа иллюзии состоит в том, чтобы выразить невозможность в терминах такого явления как непрерывный подъем или спуск. Примером является лестничный пролет, изображенный на рисунке 11. Каждая часть данной структуры представляет обычные ступеньки, но вся картина целиком – противоречива: лестница постоянно ведет вниз при движении по часовой стрелке.
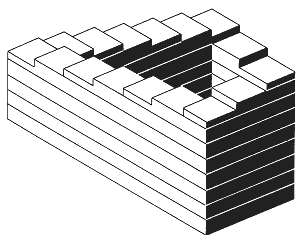
Рисунок 11.
Настоящие объекты, особым образом спроектированные, рассматриваемые с определенных углов, могут создавать то же самое впечатление, что и противоречивые рисунки. Фотография модели такого типа, воспринимаемой как невозможная лестница, представлена на рисунке 12. В действительности дальняя правая часть лестницы была гораздо ближе к камере и гораздо выше ступеньки, которая на фотографии выглядит выше. Иллюзии другого типа, созданные подобным образом, описаны Килпатриком (Kilpatrick) в 1952 году.

Рисунок 12.
Ссылки:
Escher, M.C. (1954): Catalogus 118; Stedelijk Museum, Amsterdam.
Kilpatrick, F.P. (1952): "Elementary demonstrations of perceptual phenomena". In Human Behavior from the Transactional Point of View. Hanover, N.H.: Institute for Associated Research.
Невозможный куб Эшера
Когда Эшер начал работать над литографией "Выпуклость и вогнутость" в 1955 году, он уже совершенно точно был знаком с двойственностью куба Некера. Он искал способы объединения двух постоянно меняющихся ориентаций куба в объект, который бы допускал одновременно две взаимоисключающие интерпретации. Он достиг успеха в 1957 году, создав "Куб с магическими лентами" (рисунок 16). Промежуточные версии этой картины показывают, что Эшер уже был немного знаком с невозможными трибарами.

Рисунок 13. М.К. Эшер, 1985 г. (фото Бруно Эрнста)
Год спустя Эшер открыл невозможных куб, в котором куб Некера больше не был двойственным объектом, а стал "стабильным" невозможным объектом. Тем самым он обратил внимание на открытия, которые он сделал в области невозможных соединений брусков. Его первые наброски в этой области не используют невозможного перекрытия, но в финальном результате, которые он использовал в картине "Бельведер", они присутствуют. Замысловатая конструкция этой впечатляющей картины (на ранних стадиях известная как "Призрачный дом") заслуживает более пристального рассмотрения.
В главе 5 мы рассмотрели принцип, в соответствии с которым можно создать большое количество невозможных кубоидов. Большинство из них (включая и ту версию, которую Эшер использовал в картине "Бельведер") достаточно сложны для зрителя. ГЛАЗ пытается воссоздать некоторые из них, но наталкивается на вопиющие противоречия, заложенные в геометрических деталях объекта. Лишь гармоничным сочетанием невозможных элементов с дополнительной информацией о перспективе можно целиком передать всю красоту невозможного куба и, следовательно, реальность и великолепие невозможности!
Рисунок 14. Анализ структуры Бельведера Эшера (см. Рис. 18), литография, 42.2 x 29.5 см, 1958
Эшер был мастером такого искусства. Исследуя более внимательно его "Бельведер" (рисунок 18), мы поражаемся ненавязчивостью невозможного кубоида в центре композиции. Его горизонтальные плоскости длинные и узкие, в то время как части, имеющие пространственные противоречия, лежат далеко друг от друга и замаскированы. Это не то решение, которое мы ожидали получить, так как кажется, что скрыть важные элементы, которые формируют объект, невозможно. Эшер делает следующий шаг в этом направлении, скрывая потолок за арками и пол за балюстрадой. Что остается от невозможного кубоида показано на рисунке 14. Верх и низ от этой проволочной модели Эшер рисует сплошными детализированными блоками, которые усиливают реальность картины в целом и в то же время обращают внимание на противоречие в ориентации верха и низа кубоида. Таким образом, верхний этаж выглядит лежащим перпендикулярно нижнему этажу. Эффект усиливается еще и тем, что женщина на верхнем этаже и мужчина на нижнем смотрят в разные стороны. Необходимо как минимум четыре колонны, чтобы соединить верхнюю и нижнюю плоскости невозможного куба, где только две из них будут "невозможными". В данном случае Эшер использует восемь колонн, шесть из которых образуют невозможные соединения. Лестница, приставленная от нижнего этажа к верхнему, представляет еще одно такое соединение, которое подчеркивается двумя фигурами, взбирающимися по ней. Нижняя фигура выглядит находящейся внутри кубоида, а верхняя фигура – снаружи. Эшер использует все эти приемы, чтобы внести в свою картину большую степень невозможности, чем было изначально получено сокрытием противоречащих друг другу элементов. Ясно, что художник разработал композицию очень тщательно, чтобы передать удивительную природу невозможного кубоида настолько реалистично, насколько это вообще возможно.
Рисунок 15. М.К. Эшер, предварительный набросок картины "Куб с магическими лентами"
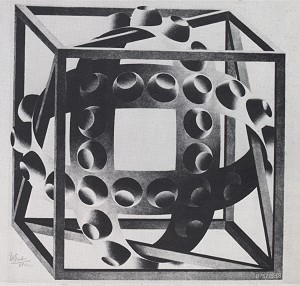
Рисунок 16. М.К. Эшер, "Куб с магическими лентами", литография, 30.9 x 30.9 см, 1957
Рисунок 17. Сандро дель Прет, рисунок карандашом, 36.5 x 25.2 cm, 1985. Бельведер Эшер может рассматриваться в виде соответствующей конструкции, у которой отдельные соединения искривлены.

Рисунок 18. М.К. Эшер, "Бельведер", литография, 46.2 x 29.5 см, 1958
Эшер и Пенроуз
В письме к своему сыну Артуру 24 января 1960 года Эшер описал как статья Пенроузов вошла в его поле зрения. В то время он "работал над новой картиной, на которой были изображены лестничные пролеты, которые воспринимались восходящими или спускающимися в зависимости от того, как на них смотреть. При разглядывании по кругу изгибы лестниц принимали форму спирали, исчезающей в облаках наверху и в Аду внизу. Не так как с моими лестницами: их форма замкнутая круговая конструкция, скорее напоминающая змею кусающую свой хвост. И еще они могут быть нарисованы корректно в перспективе: каждая ступенька выше (или ниже) предыдущей. Несколько человеческих фигурок движутся по лестницам в обоих направлениях. Фигуры с одной стороны идут постоянно наверх, в то время как фигуры на другой стороне лестницы бесконечно спускаются. Я открыл данный принцип в статье, которую мне прислали, и в которой я сам назван как создатель различных 'невозможных объектов'. Но я не был знаком с непрерывной лестницей, небрежный набросок которой автор включил в статью, хотя я использовал ранее другие примеры из статьи."
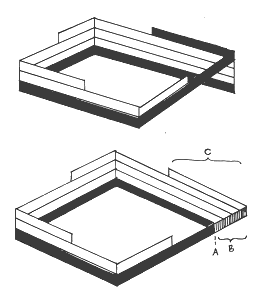
Рисунок 19 (сверху) и рисунок 20. Конструкция с картины Эшера "Восхождение и спуск" может быть интерпретирована двумя способами. Сам Эшер объяснял ее в терминах рисунка 19, который не является невозможным объектом. Я привел такое же описание в моей книгу "Магическое зеркало М.К. Эшера".
Работы Эшера не оставили явных доказательств того, что он знал о невозможном трибаре до прочтения статьи Пенроузов. Тем не менее, наброски "Куба с магическими лентами" показывают, что он, конечно же, был поглощен подобными вопросами. Но именно бесконечная лестница заворожила Эшера более всего, несмотря на "небрежный набросок". Впоследствии (18 апреля 1960 года) он написал обоим Пенроузам: "Несколько месяцев назад мой друг прислал мне фотокопию вашей статьи... Ваши рисунки 3 и 4, "непрерывной лестницы", были новыми для меня, и они настолько захватили меня, что сподвигли меня создать новую картину, которую я хотел бы отправить вам в знак моего уважения. Если вы публиковали другие статьи о невозможных объектах или на смежные темы, или если вы знаете другие подобные статьи, я был бы очень благодарен, если бы вы прислали дополнительную информацию." Пенроуз ответил письмом с благодарностями и статьей о новом типе невозможного объектов. Картина, которую Эшер отправил? была "Восхождение и спуск" (рисунок 21), наименее оригинальная из четырех картин Эшера с невозможными объектами, которая была не более чем "раскрашенная" версия наброска Пенроуза. Сам Эшер никогда не понимал, как на самом деле возникла невозможность. В "Магическом зеркале М.К. Эшера" я предложил анализ изображения на основе собственных объяснений Эшера. Только годы спустя я понял, что "Восхождение и спуск" Эшер интерпретировал не как невозможный объект, а скорее как искаженную фигуру, которая может быть построена в трех измерениях, в то время как лестница Пенрозов по-настоящему невозможна.

Рисунок 21. М.К. Эшер "Восхождение и спуск", литография, 32.5 x 28.5 см, 1960
Эшер поместил свою лестницу на крышу здания. Насколько он понимал, вполне возможно обернуть ленту спиралью вокруг внешней части здания. При помощи сужения элементов, равномерно распределенного по всем углам и плоскостям картины, стало возможным создать иллюзию непрерывного лестничного пролета, как показан о на рисунке 19. Ни в одном месте лестницы нет разрыва. С другой стороны, на рисунке 20 все четыре стороны конструкции лежат на одной горизонтальной плоскости. Заштрихованная часть ленты должна заканчиваться в точке A, но добавив длины B, мы создаем (невозможное) соединение с лестницей в точке C – и это невозможный объект, который обсуждается в статье Пенроузов и который, исполненный в виде реальной модели, сформирует лестницу с разрывом. Естественно, невозможно сказать, какой из двух методов используется в картине "Восхождение и спуск". Ясно только то, что разница между возможным и невозможным очень мала в такой реалистичной композиции. Эшер использовал трибар Пенроуза в своей литографии "Водопад" (1961) (рисунок 22). Создав серию эскизов, каждый из которых мог сформировать привлекательный невозможный объект, он пришел к трибару, который выглядит естественно в реалистичной детализированной обстановке. Геометрическая невозможность здесь усиливается физической невозможностью. Эшер сформировал конструкцию вечного двигателя первого порядка: вода на его картине заставляет вращаться мельничное колесо, вырабатывая энергию из ничего!

Рисунок 22. М.К. Эшер "Водопад", литография, 38 x 30 cm, 1961
"Водопад" стал последней из четырех невозможных картин, созданных Эшером. По его мнению, успешно изобразив специфическую природу невозможных объектов, он вернулся к теме, которая его неудержимо тянула, и которую он считал своей специальностью, а именно, к регулярному заполнению плоскости. Эшер первым нарисовал невозможный куб. Он также знал, как пластично изобразить множество других невозможных объектов, почти в форме рассказа. Возможно главное значение для невозможных объектов заключается в том, что его картины получили большую популярность и мировое признание, расширив наш мир.

Рисунок 23. М.К. Эшер, наброски невозможных объектов

Рисунок 24. Матье Хемекерс, "Водопад Эшера повернутый на 45°", рисунок карандашом, 29 x 29 cm, 1985
Вилка Дьявола
Невозможные объекты с двойственными контурами, характеризующиеся тем, что они не могут быть раскрашены (рисунок 25), были созданы Оскаром Реутерсвардом задолго до 1958 года. Однако, только в 1964 году к этим объектам было привлечено внимание в короткой статье Д.Х. Шустера (D.H. Schuster), посвященной невозможным объектам, которые с тех пор стали известны как "вилка дьявола".
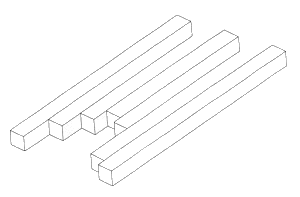
Рисунок 25. Оскар Реутерсвард, структура три-на-семь
Новый тип двойственной фигуры: цепное соединение / горизонтальная скоба
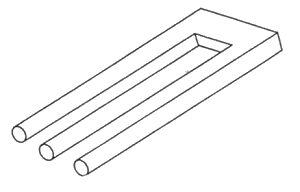
Рисунок 26.
"Фигура напротив (рисунок 26), которая недавно была опубликована в рекламной продукции Недели Авиации и Космических Технологий (80, 1964), приведена здесь по причине того, что она является новым типом двусмысленных фигур. В отличие от других двусмысленных рисунков и геометрических фигур, таких как утка-кролик Ястроу, жена-и-мачеха Хилла, отец-и-отчим Ботвиника (мужская версия изображения Хилла), куб Некера, лестница Шрёдера и книга Маха, здесь значительную роль в восприятии и интерпретации играет смещение точки фокусировки взгляда. Если зритель фокусируется на левую часть фигуры с обычного расстояния, как при чтении книги, он видит три колонны, и правая часть рисунка остается размытой и нечеткой. Если он фокусируется на правой стороне рисунка, то видит U-образный объект подобный скобе, расположенной горизонтально. И только если он посмотрит в середину рисунка или позволит медленно взгляду перемещаться по фигуре, он придет к пониманию, что смотрит на 'невозможный объект', подобный невозможным иллюзорным фигурам, описанным Пенроузами."
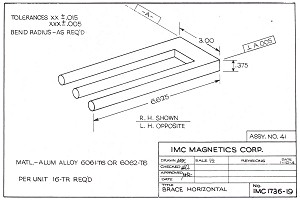
Рисунок 27.
Вскоре появилось множество вариаций на тему "вилки Дьявола" (рисунки 27 и 28). Дальнейшее понимание таких объектов Оскаром Реутерсвардом привело его к созданию более сложных структур, таких как на рисунке 25 с тремя брусками выглядящими как семь и на рисунке 29, чья истинная природа в качестве "вилки Дьявола" опознается не так легко.
Рисунок 28.
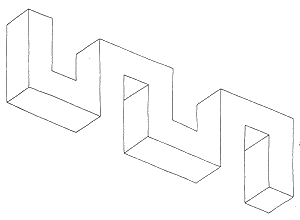
Рисунок 29. Эта извилистая фигура обладает теми же свойствами, что и более поздняя вилка Дьявола.
Назад во времени
Хотя, можно сказать, что история невозможных фигур началась с 1934 года, некоторые из них появились до этой даты. Одни были созданы в шутку, как в случае картины Марселя Дюшампа, другие - неосознанно или полу-осознанно в отчаянной попытке представить стереографические элементы приемлемым способом. Последние позднее расценивались как несовершенства перспективы, однако, сегодня мы можем их рассматривать с новой точки зрения.
В 1916/17 годах Марсель Дюшамп (Marcel Duchamp) превратил рекламу Sapolin, известного производителя красок, в оммаж своего друга Аполинара (Apollinaire), удалив и добавив различные буквы (рисунок 30). Он также трансформировал раму кровати с помощью нескольких мазков белой краски в не очень убедительную версию трех- и четырехбылочника. Сам Дюшамп никогда больше не двигался в данном направлении. Чтобы найти еще один пример, нам надо отправиться еще на 150 лет назад.

Рисунок 30. Марсель Дюшамп, "Apolinere enameled"; 1916-17, Музей Изобразительных Искусств Филадельфии
Четырнадцатая тюрьма Пиранеси
Джованни Батиста Пиранеси (Giovanni Battista Piranesi) (1720-78) родился в Венеции. Хотя он обучался архитектуре, большее внимание в творчестве он уделял гравюре. Он опубликовал более тридцати книг по архитектуре, по большей части полемики, иллюстрированные сотнями рисунков архитектуры в стиле неоклассицизма. Его бурная деятельность не представляет особого интереса сегодня. Исключением является лишь его серия гравюр "Тюрьмы" - странные, таинственные и мистические изображения тюремных застенков. "Invenzioni capricci di carceri" - набор из четырнадцати пластин, впервые опубликованные в 1745 году в третьей части его обширного списка публикаций. Позже он пересмотрел все гравюры и добавил две новые, которые были вновь опубликованы в 1760 году под заголовком "Carceri d'invenzione" (Imaginary Prisons).
Хотя фантастическое изображение тюрем не было чем-то необычным в те дни, картины Пиранеси выделяются оригинальностью и мощью авторского представления нереальных, и часто невозможных, комнат в стиле, которые стилистически идут дальше неоклассицизма.
В четырнадцати тюрьмах Пиранеси использовал совмещение нескольких плоскостей в одной как одно из средств, которое он сознательно использовал для создания необычных, невозможных пространств, однако без должного понимания. Тем не менее, он достиг нового метода построения пространственных противоречий.

Рисунок 31. Джованни Батиста Пиранеси, "Тюрьмы, пластина XIV", исправленная версия, 1760
О его гравюрах писали многие авторы, которые обсуждали содержащиеся в них противоречия. Некоторые даже видели в них иллюстрацию неевлклидовой геометрии, а профессор J.H. van den Berg сделал их основой для одной важных частей своей работы "Metabletica of Matter." Однако, данные картины имеют мало общего с неевклидовой геометрией. Сознательно стремясь изобразить пространства сложные (если не невозможные) для анализа, Пиранеси, тем не менее, зависел от традиционных соглашений того времени по изображению трехмерного пространства на плоскости. Он достиг своей цели, включив в картину неясные и даже противоречивые пространственные детали. Так он вошел на территорию невозможных объектов, множество примеров которых может быть найдено в его Тюрьмах. Наиболее очевидный пример виден на вышеупомянутой четырнадцатой гравюре, воспроизведенной здесь в исправленном виде от 1760 года (рисунок 31). Длинная стена с тремя арками начинается в левой части и пропадает в центре картины. В точке B (см. Рисунок 32) верхняя часть стены продолжается дальше, в то время как нижняя часть находится ближе к переднему плану, чем верхняя часть. Таким образом, создана множественная плоскость. Пиранеси усиливает этот эффект добавлением лестничного пролета C, который идет параллельно стене и все же исчезает позади нее. Я проиллюстрировал основные особенности картины максимально точно, но схематично, на рисунке 32, на котором невозможный объект виден сразу и совершенно ясно.
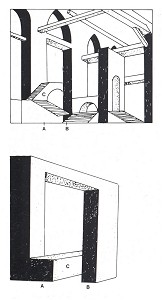
Рисунок 32. Анализ картины Пиранеси "Тюрьмы, пластина XIV"
"Ложная" перспектива Хогарта
Другая картина, которая появилась примерно в то же время, хотя и совершенно иная по своей природе, также имеет важное значение в связи с невозможными объектами.
Английский художник и гравер Уильям Хогарт (William Hogarth) (1697-1764) известен как ведущий моралист среди художников Англии восемнадцатого века, Он имеет такую репутацию, которая заставляет нас забыть, что он создал множество замечательных картин в стиле итальянских мастеров живописи того времени. "Ложная перспектива" - гравюра на медном листе 1754 года (рисунок 33) – могла бы сделать его "отцом невозможных объектов", если бы не тот факт, что основной целью данной композиции было продемонстрировать типовые ошибки неумелых рисовальщиков. Он разъясняет в заголовке: "Тот, кто будет рисовать без надлежащих знаний о перспективе, будет склонен из изображению подобных нелепостей, как на этом фронтисписе". Здесь также присутствует склонность к морализаторству, хотя в данном случае и не направленная на популярные социальные грехи того времени.

Рисунок 33. Уильям Хогарт, "Ложная перспектива", литография, 1754
Рыболов на переднем плане справа стоит на плиточной мостовой, для которой неверно выбрана точка схождения, вследствие чего она выглядит вертикальной, но это не имеет ничего общего с невозможными объектами. Позади рыбака дощатая стена сочетает в себе сразу две ориентации (см. главу 5). Над ним висит вывеска, но ее пространственная конфигурация противоречива, так как перекладина и ее подпорка прикреплены к двум разным зданиям. Сама вывеска частично перекрыта деревьями, что указывает нам на то, что вывеска находится еще дальше. Женщина, высунувшись из окна свечой поджигает трубку путника. А путник находится на холме в сотнях метров от нее...
Оставим другие "нелепости" в покое. Вы можете заметить, что Хогарт не использует каких-то определенных невозможных объектов. Тем не менее, при создании своей картины он использовал те же пространственные противоречия, с которыми мы встречались в конструкциях настоящих невозможных объектов.
Фреска в Бреде
На картине Брейгеля "Сорока на виселице" (1568, рисунок 34) мы отчетливо видим невозможный четырехбалочник. Меня бы не удивило, если художник намеренно изобразил что-то из ряда вон выходящее. В попытке понять странные пространственные взаимосвязи картины, мы сначала пытаемся увидеть виселицу в виде искривленных брусков. Но если мы попытаемся нарисовать брусок вывернутый таким образом, мы не получим тот же результат, что Брейгель. Здесь мы снова видим случайное, но осознанное открытие.

Рисунок 34. Питер Брейгель, фрагмент из "Сорока на виселице", Hessisches Landesmuseum, Дармштадт
Неизбежно наша увлеченность поисками невозможных объектов заставит нас попытаться обнаружить такие объекты в исторических произведениях, хотя вероятность мала. Тем не менее, в некоторых случаях, поиски будут успешны, как в случае с фреской в церкви Девы Марии (или Grote Kerk) в г. Бреда. Это доказательство невинного создания невозможного объекта до 1934 года дает возможность для поиска невозможных объектов в прошлом.
В 1902 году в церкви Grote Kerk в г. Бреда (Голландия) под более поздними слоями была обнаружена фреска размером 2.7x2.5 метров. Замечательно сохранившаяся, она показывает сцену Благовещения руки мастера пятнадцатого года (см. цветную репродукцию в начале главы). Сцена ограничена двумя арками, поддерживаемыми тремя колоннами. Две внешние колонны изображены на переднем плане, в то время как центральная колонна заканчивается на заднем плане за столом. В результате плоская стена находится в двух плоскостях одновременно. Первый историк, описывавший фреску, обратил вниманием на эту любопытную особенность, описав ее как "красная колонна, неправильно расположенная в перспективе". Однако, художник точно знал, почему он сделал эту ошибку: он не хотел, чтобы картина была разделена колонной на две части. (Известны и другие случаи изображения Благовещения с укороченной центральной колонной).
Цветная репродукция фрески свидетельствует об очень плохом ее состоянии в наши дни.
Обстоятельства, объясняющие непреднамеренные невозможные объекты.
Человек начал сохранять свои визуальные впечатления в графической форме очень давно. Конечно, все графические представления по определению неполны и выборочны. Но в течение этого начального (и, тем не менее, длительного) периода воспроизводились только пиктографические элементы. Однако, когда объекты стали изображаться более детально, добавились стереографические элементы: человеческие фигуры стали тремерными, как и их ближайшее окружение.

Рисунок 35. Лоренцо Монако (Lorenzo Monaco), часть из "Коронация Девы Марии", 1413, Уффици, Флоренция
Стремление к более точному изображению пространства становилось все сильнее, и художники изобрели несчетное количество приемов и трюков для представления упрощенной формы увиденных объектов на двухмерной поверхности. Такой процесс может быть найден в любой культуре, в которой простое представление развилось в "искусство". И в некоторых случаях это привело к процветанию схожих идеалов в искусстве: Греция в 5-м веке и Италия в районе 1425 года пришли к центральной перспективе, в то время как в Японии предпочитали аксонометрическую перспективу. Мы можем ожидать нахождения неосознанных невозможных объектов в тех культурах, где установилась самостоятельная система представления пространства. Такие системы позволяют художникам воспроизводить пространственные взаимосвязи с высокой степенью точности, и там, где они ошибаются, возникают пространственные противоречия. На рисунках 35 и 36 показаны две работы: одна - Лоренцо Монако (Lorenzo Monaco), вторая – Пьетро Лоренцетти (Pietro Lorenzetti), относящихся к периоду до изобретения центральной перспективы. Оба художника пытались изобразить плоский пол, но ни один из них не добился успеха, создав двусмысленность. В обоих случаях, ясно, что внутренняя задняя стена в нижней половине картины выглядит гораздо дальше наверху, и при проецировании вперед она выглядит как внешняя стена. Таким образом, человеческие фигуры выглядят сидящими одновременно и внутри и снаружи. Даже более поздняя картина из Охрида (рисунок 37) содержит пространственное противоречие в изображении трона Девы Марии. Балдахин наверху пространственно согласуется с основанием трона при помощи колонны в левой части трона. Иначе дело обстоит с правой колонной: художник робко уклонился от перекрывания фигуры Марии колонной, вследствие чего возникло пространственное противоречие. Самый ранний известный невозможный объект изображен на миниатюре 11 века (рисунок в начале главы).

Рисунок 36. Пьетро Лоренцетти (Pietro Lorenzetti), запрестольный образ, первая половина XIV века, Уффици, Флоренция

Рисунок 37. Благовещение, византийская игра, начало XIV века, Национальный музей, Охрид
Невозможные фигуры как признак культурных изменений
Центральная перспектива вместе с формой восприятия, которая сопровождает ее, является основным правилом представления пространства, которое мы не можем так просто отбросить без длительных раздумий. Мы живем с этим правилом более пяти с половиной столетий и рассматриваем все представления согласно критериям перспективы.
Примерно около 1900 года в искусстве появились новые тенденции и движения. Среди многих особенностей, отличавших те движения, наиболее поразительным является отказ от традиционного пространственного представления. Одно достаточно четкое направление, которое впоследствии вылилось в то, что сегодня известно как оп-арт, концентрировалось на оптических эффектах и исследовало особый путь, которым наш мозг обрабатывает информацию. Тот факт, что оп-арт рассматривается как мимолетное явление в истории искусства свидетельствует, в основном, об избирательности авторов, пишущих об искусстве, многие из которых отказались признать, что оп-арт основан на работе нашего восприятия. Тем не менее, оп-арт получил широкое признание в прикладном искусстве и мире рекламы.
В то время как невозможные объекты имеют некоторые точки контакта с оп-артом, скорее всего они вызывают интерес по более веским причинам. Они не дают никаких оснований для отмены законов представления пространства. Напротив, невозможные объекты не только принимают эти законы, при случае нарушая их, но и эксплуатируют их для создания тугой пространственной связки. Будущее покажет, является ли увеличивающийся интерес к невозможным объектам чем-то большим, чем просто мимолетный художественный элемент. Однако, даже сегодня можно утверждать, что мы рассматриваем их не просто как художественный элемент, а скорее как фундаментальное переосмысление западного образа мышления и накопленного опыта. В 1934 году общество еще не было готово к работам Оскара Реутерсварда. Лишь через 25 лет работы Эшера очаровали широкие слои общественности. Стиль рисунков Эшера был достаточно традиционен, и поэтому не его стиль рисования привлек столь широкий интерес, а сенсационный предмет, изображенный на картинах, исследовавший функционирование нашего мозга. Невозможные объекты не принадлежат только миру искусства, скорее они находится в области математики. Невозможные объекты могут быть созданы по-дилетантски неопытно, но они все равно вызывают восхищение даже у тех, кто далек от геометрических фигур. Они излучают ауру саморазоблачения, которое непосредственно обращается новоприобретенной человеческой способности восприятия. Невозможные объекты являются признаком культурных изменений.
Недоразумения вокруг невозможных объектов
В науке есть множество теорий известных широкой публике – своебразных "черных дыр", которые захватили всеобщее внимание. Показательными примерами являются: теория относительности Эйнштейна, четвертое измерение, неевклидова геометрия, которые и сегодня очень популярны. К сожалению, после всех упрощений теорий, при их популяризации остается лишь малое количество от содержания исходных теорий. Таким образом, некоторые авторы предложили связать "невозможные объекты" с научными понятиями, покрытыми тайной.
Во вступительном слове к книге Реутерсварда "Omöjliga figurer i färg" Carlo Bresti исследует попытки создания четырехмерных фигур. Он приходит к выводу в отношении невозможных фигур, что они являются прорывом в искусстве: "Поскольку полет двадцатого века привел нас из трехмерности на тупиковый путь двухмерных областей, следующий век будет лететь в противоположном направлении, в область четвертого измерения, где бесконечные лестницы и треугольники с суммой углов в 270 градусов будут обычными элементами."
Даже если мы добавим четвертое измерение, бесконечная лестница все равно останется невозможным объектом до тех пор, пока в четвертом измерении сумма углов треугольника будет равняться 180 градусам. На самом деле искать четырехмерный эквивалент невозможного объекта – верное решение. Роджер Пенроуз начинал изыскания в данном направлении в 1976 году, но не опубликовал никаких результатов. Скот Ким (Scott E. Kim), который переписывался с Пенроузом по данному вопросу, в 1978 году написал статью, в которой дал детальное описание невозможного четырехмерного трибара вместе с инструкциями, как воспроизвести его в трех измерениях. Хотя этот "четырехмерный рисунок" (который воспроизводится в трех измерениях) скорее всего мало что значит без детального описания того, как он возник, здесь мы воспроизвели иллюстрацию его проволочной модели (рисунок 38). Мы также ждем описание модели невозможной лестницы в четырех измерениях, которую автор статьи обещал представить общественности.
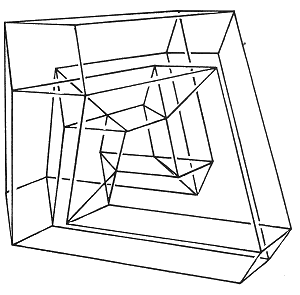
Рисунок 38.
Мы уже отмечали, что профессор J.H. van den Berg стремился установить параллели между "Тюрьмами" Пиранеси и неевклидовой геометрией. Реутерсвард занимался тем же, когда писал о своих невозможных объектах. Неевклидовая геометрия также была одной из тем обсуждения в ходе моей переписки с бельгийским художником Матье Хемекерсом (Mathieu Hamaekers). В связи с его превосходными моделями невозможных объектов, составленных из изогнутых и скрученных брусков (см. главу 7), он писал: "Разработанные мной методы основаны на геометриях Римана и Лобачевского. Можно было бы дать каждой культуре свою эстетику, так как неевклидовые модели предполагают бесконечное количество вариантов. Важно, что каждая культура должна иметь возможность представить свою индивидуальность даже в двадцать первом веке. Такое же моделирование может быть компромиссом между органическим и математическим."
В то время как многие из нас имеют смутное представление о четвертом измерении, принципы неевклидовой геометрии заслуживают более подробного рассмотрения.
Евклид основал свою геометрическую систему на пяти аксиомах (недоказуемых предположениях, принимаемых за истину). Аксиомы – непременное условие в любой системе логики, каждое доказательство должно быть основано на предыдущих доказательствах и утверждениях (в случае евклидовой геометрии – на аксиомах). Аксиомы необходимо использовать экономно, чтобы утверждение, которое может быть доказано при помощи предыдущих аксиом, само не было аксиомой.
Пятая аксиома Евклида занимает особое место. Она формулируется следующим образом: "Через точку P, не принадлежащей заданной прямой l, в плоскости, на которой лежат прямая l и точка P, возможно провести только одну линию параллельную l."
До первой четверти XIX века ведущие математики были убеждены, что пятая аксиома может быть доказана при помощи предыдущих четырех аксиом, хотя все попытки доказательства оказались несостоятельными.
В 1829 году Лобачевский показал, что отбросив пятую аксиому Евклида можно создать совсем другую геометрию. Он заменил пятую аксиому тезисом, что через точку P, не принадлежащую прямой l, невозможно провести линию, параллельную l. Хотя эта аксиома противоречит нашему повседневому опыту, тем не менее, на этой основе можно создать геометрию без внутренних противоречий. Четвертью века позже появился Риман с геометрией, в которой пятая аксиома Евклида была заменена постулатом, что через точку P можно провести бесконечное количество линий, параллельных линии l. Изучая данные геометрии, мы видим, что их пятые теоремы приводят к разным последствиям. Так, в Евклидовой геометрии сумма углов треугольника всегда равна 180 градусам. В геометрии Лобачевского сумма углов треугольника всегда меньше 180 градусов, а геометрии Римана – всегда больше 180 градусов. Отметим, что это не оказывает никакого влияния на невозможные объекты и их реализацию в виде модели. В то время как геометрические модели могут быть точно описаны в терминах евклидовой геометрии, сами невозможные объекты не повинуются даже неевклидовым геометриям. Они продолжают восхищать нас своей формой, приводя в замешательство нашу зрительную систему.
Также были предприняты попытки установить связь между невозможными объектами и парадоксамив области логики. Если взять термин "парадокс" в самом широком смысле, то, без сомнения, можно говорить о логических и зрительных парадоксах. В случае с невозможными объектами, мы попадаем в категорию зрительных парадоксов.
Концентрация на структуре логического (или даже линвистического) парадокса не приводит к лучшему пониманию невозможных объектов. M.J. Cresswell пытался определить невозможные объекты, используя термины логики. Хотя это был и интересный подход, он не смог пролить нового света на природу невозможных объектов. Более того, очевидно, что он не был информирован в области функционирования зрительной системы для исследования невозможных объектов. В заключении своей работы, он просто выражает надежду, что новый свет на проблему может быть пролит только с точки зрения логики и семантического анализа.

Рисунок 39. Сандро дель Прет "Извилистая лестница на Бельведер – 2", рисунок карандашом
