Невозможные плитки
Диего Урибе
Аннотация. Невозможные фигуры являются частью нашего визуального языка. В данной статье описывается набор плиток, используемых для конструирования невозможных фигур (НФ), состоящих из брусков квадратного сечения, соединенных друг с другом под прямыми углами. Данный класс НФ включает в себя "невозможный треугольник". Статья начинается с описания метода создания набора плиток. Далее НФ, составленные из плиток, разделяются на три класса: НФ без пресечения брусков, НФ с пересечениями брусков и НФ с двойственной точкой обзора. Количество плиток в подмножествах плиток из всего множества, необходимых для создания фигур каждого следующего класса все больше и больше. Подмножество плиток, необходимое для создания НФ без пересечения брусков, используется для простейшего алгоритма распознавания, является ли фигура невозможной. Далее при помощи невозможных плиток описываются основные невозможные фигуры, использованные М.К. Эшером в своих работах. В заключение невозможные плитки используются в качестве средства для создания комбинаторных мозаик (пазлов), для регулярного разделения плоскости, фракталов из невозможных фигур и в качестве эскизного средства для создания "реально выглядящих" НФ. Таким образом, набор невозможных плиток дает интуитивный путь характеристики НФ, изучаемых различными дисциплинами, обеспечивая связь между математикой, психологией и художественным искусством.
Невозможные фигуры.
Со времени первого использования Оскаром Реутерсвардом [1] и Морис Эшером [2] в своих произведениях НФ, они стали неотъемлемой частью нашего визуального языка, давая художникам, работающим в данном направлении необычное представление глубины пространства.
Впервые о НФ было рассказано Роджером и Лайонелом Пенроузами в статье в британском журнале психологии[3]. В статье Пенроузов рассказывалось о двух типах НФ: трибар (также известный под названием "невозможный треугольник") и бесконечная лестница. Обе фигуры были основаны на использовании одной и той же хитрости, обманывая восприятие и заставляя верить, что две точки, совпадающие на изображении, должны совпадать и в трехмерном пространстве. Этот эффект может быть продемонстрирован при помощи кубической координатной сетки и замкнутой фигуры, построенной по узлам этой сетки (рис. 1).
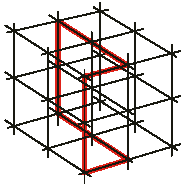
Рис. 1. Кубическая сетка и замкнутая фигура,
построенная по узлам этой сетки.
Рассмотрим точки на рис. 1, где линии замкнутой фигуры пересекаются. В этой точке возможны три варианта расположения элементов фигуры: а) – вертикальная линия находится спереди горизонтальной; b) – вертикальная и горизонтальная линии пересекаются; c) – вертикальная линия находится позади горизонтальной. Вариант a дает возможную фигуру, а варианты b и c – невозможные (рис. 2.)[4].
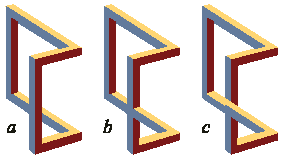
Рис. 2. Три интерпретации замкнутой фигуры с
рис. 1, реализованные в виде фигур,
составленных из брусков квадратного
сечения.
Создание набора плиток
Рис. 2 изображен в изометрической проекции. Предлагается набор плиток, стороны которых располагаются по сторонам сетки, определяющей расположение ортогональных осей в трехмерном пространстве. У каждой плитки может быть закрашена одна или более сторон и/или один или более углов, которые являются частью бруска квадратного сечения. Также плитка может быть и пустой, то есть у нее не будет закрашенных углов и сторон. Изображенные таким образом фигуры выглядят так, как если бы мы смотрели на них сверху. Стороны фигур раскрашены таким образом, что они освещаются источником света, находящимся сверху слева. Таким образом, стороны, направленные вверх, окрашиваются наиболее ярким цветом (желтым), стороны, направленные влево – более темным (голубым), а стороны, направленные вправо, – еще более темно цветом (коричневым). Хотя окрашивание сторон необязательно, это облегчает восприятие.
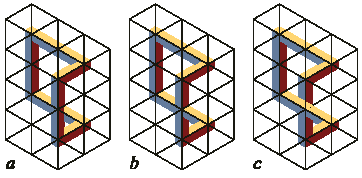
Рис. 3. Три фигуры с рис. 2, изображенные в
изометрической проекции с предложенным
набором плиток.
Возникает вопрос нахождения всех минимального набора возможных комбинаций закрашенных сторон и углов плиток достаточных для построения невозможных (или возможных) фигур, типы которых представлены на рис. 3. Ответ зависит от двух факторов: тип фигуры, который необходимо получить и определения концепции "фундаментальной плитки".
Обратимся снова к фигуре на рис. 1. Снова обратим внимание на точку, где линии фигуры пересекаются, и получение трех интерпретаций фигуры на рис. 2. Тип фигуры определяется взаимным расположением вертикальной и горизонтальной линий фигуры в точке пересечения. Если элементы фигуры находятся на разных уровнях, то есть один элемент заслоняет другой (рис. 2a и 2c), то для такого типа фигур определено некоторое множество плиток; если элементы соединяются (рис. 2b), то для таких фигур определено свое множество плиток. Последнее множество, являющееся подмножеством предыдущего [5, 6], показано на рис. 4
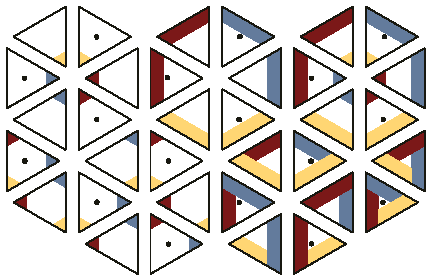
Рис. 4. Множество плиток необходимое для
конструирования невозможных или возможных
фигур, состоящих из брусков, расположенных
под прямым углом друг к другу. Получаемые
при помощи данного множества структуры не
имеют пересечений брусков на разных
уровнях. Дублирующие плитки и точки в
центрах плиток приведены для наглядности и
в дальнейшем будут устранены.
На рис. 4. плитки сгруппированы согласно количеству окрашенных углов и/или сторон: плитки с одной, двумя, тремя окрашенными сторонами, с одним, двумя, тремя окрашенными углами и с одним окрашенным углом и окрашенной стороной. Некоторые плитки повторяются; у одной из повторяющихся плиток в центре изображена точка, у другой – нет. Ни повторение плиток, ни изображение точки внутри плитки не является обязательным, а использовано только ради наглядности.
Задаваясь точкой обзора фигуры и окрашивая стороны фигуры согласно принятому освещению, получается набор всех доступных комбинаций плиток с окрашенными сторонами и углами. Например, не будет плиток с окрашенной одним цветом стороной и противоположным углом, а также не будет получено и шести возможных комбинаций плиток с окрашенными одним цветом двумя сторонами, так как такие плитки появляются только в случае рассмотрения фигур с пересекающимися брусками на разных уровнях.
Теперь о концепции "фундаментальной плитки". Рассмотрим центральную плитку на рис. 5а, именно она в данном случае формирует треугольник Пенроуза. Однако подобный треугольник, хотя и большего размера, получен при помощи другого набора плиток (рис. 5b).
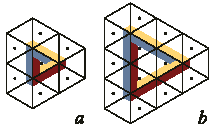
Рис. 5. Фундаментальной плиткой является
такая плитка, которая не может быть
заменена группой других плиток.
Центральная плитка на рис. 5a не является
фундаментальной, так как может быть
заменена четырьмя центральными плитками на
рис. 5b. В свою очередь центральная плитка
на рис. 5b с тремя окрашенными углами не
является фундаментальной.
Центральная плитка на рис. 5a не является фундаментальной, так как она может быть заменена группой других плиток с теми же топологическими свойствами. Обратите внимание, что центральная плитка на рис. 5b в свою очередь тоже не является фундаментальной. Следуя данной концепции, фундаментальными плитками на рис. 4 являются лишь те, у которых окрашены одна или две стороны, а также один или два угла. Выбор плиток для игры будет являться компромиссом между количеством различных создаваемых фигур и общим количеством плиток.
Почему именно треугольники?
Не смотря на то, что идея треугольных плиток появилась естественно вытекает из использования изометрической перспективы, необходимо проанализировать удобство использования треугольных плиток.
НФ, сконструированные при помощи множества плиток, представленного на рис. 4, состоят только из двух элементов: брусков и соединений. Следовательно, существуют два подхода при создании набора плиток: подход, ориентированный на бруски, и на соединения. При подходе, ориентированном на бруски, плитки представляют каталог брусков (или их частей), а соединения образуются соединением плиток сторона к стороне. При подходе, ориентированном на соединения, плитки просто представляют собой каталог соединений. Подход, ориентированный на бруски, является более элементарным по сравнения с подходом, ориентированным на соединения. Представленный набор плиток напрямую связан с подходом, ориентированным на бруски: стороны и/или углы представляются плоскостями брусков. В данном случае треугольник наиболее экономичная форма, так как каждая из трех сторон треугольника следует одному из трех направлений трехмерного пространства. Значит, треугольники представляют собой набор элементарных элементов, при помощи которых можно конструировать фигуры, а в следующей главе треугольники будут использованы для реализации простейшего алгоритма тестирования невозможности фигуры.
Но, может быть, подход, ориентированный на соединения, имеет другие полезные свойства. Количество различных соединений меньше, чем количество фундаментальных треугольных плиток. Рассмотрим одно из соединений в центре бесконечной плоскости, разделенной на плитки (рис. 6a). Заметим, что в зависимости от выбранного угла обзора и цветовой схемы окраски брусков это соединение существует в шести различных вариантах в зависимости от ориентации. Когда мы составим каталог все возможных соединений (учитывая их различные ориентации), на основе множества плиток на рис. 4, мы получим каталог с количеством элементов большим, чем количество элементов в самом множестве: 64 соединения и 34 треугольные плитки (24 плитки, если рассматриваются только фундаментальные). Следовательно, в этом случае треугольные плитки также являются экономичнее. Подобные результаты можно получить и для неокрашенных плиток или для множеств с бóльшим количеством элементов, рассматриваемых ниже.
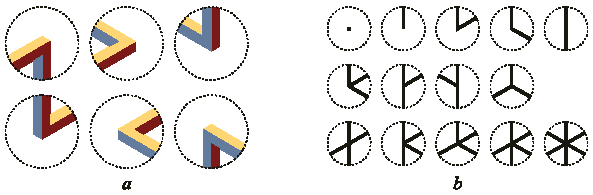
Рис. 6. a. Шесть вариантов ориентации одного
из соединений двух брусков на бесконечной
плоскости.
b. Каталог всех возможных соединений
брусков. Рассматривая ориентацию
соединений, заметим, что для первого
соединения в первой строке и последнего
соединение в третьей строке существует
только один вариант ориентации; для
последнего соединения во второй строке
возможны два варианта ориентации; для
последнего соединения в первой строке и
первого соединения в последней строке
возможны три варианта ориентации; для всех
остальных соединений возможны все шесть
вариантов ориентации.
Простейший алгоритм определения невозможности фигуры
Представим себе плоскость разбитую на треугольные плитки и окрашенную подобно шахматной доске. Рассмотрим набор плиток, представленный на рис. 4. Плитки с точками в центре будем помещать поверх черных ячеек, а плитки без точек – поверх темных. В обоих случаях цветовая схема плиток сохраняется. Полученные таким образом фигуры могут быть как разомкнутыми (рис. 7a), так и замкнутыми (рис. 7b и 7c).
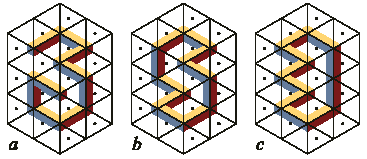
Рис. 7. Три структуры, созданные при помощи
набора плиток с рис. 4.
a. разомкнутая фигура;
b – замкнутая возможная фигура;
с – замкнутая невозможная фигура.
Проследим путь замкнутых фигур вдоль линий сетки, и будем рассматривать этот путь как последовательность подъемов и спусков, как бы путь по лестнице (рис. 8a и 8b). Фигура является возможной, если, двигаясь вдоль линий сетки по контуру фигуры мы совершим столько же спусков сколько и подъемов. В противном случае фигура будет невозможной. На рис. 8a путь поднимается на один шаг (на величину длины стороны плитки) в правой части фигуры и опускается на один шаг в левой части; на рис. 8b путь поднимается на шаг в правой части и спускается на два шага в левой части. Следовательно, фигура на рис. 7b является возможной, а фигура на рис. 7c – невозможной. Аналогичные рассуждения можно провести, рассматривая два других направления пространства: в случае возможной фигуры путь пройденный в одном направлении должен быть равен пути, пройденному в обратном направлении. Рассмотрим теперь плитки внутри пути фигуры. Подъемы мы совершаем вдоль границ плиток с точкой, а спуски вдоль границ плиток без точек (аналогично и для других направлений пространства).
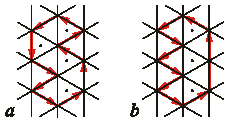
Рис. 8. Пути, соответствующие фигурам на рис. 7b
и рис. 7c, построенные по линиям сетки.
Если количество плиток с точками и плиток
без точек равно, находящихся в области
внутри пути, равны, то фигура возможна (a),
иначе – невозможна (b).
Рассмотрим теперь процесс конструирования внутренней части невозможной фигуры, чей периметр рассматривается как путь подобно рис. 8.
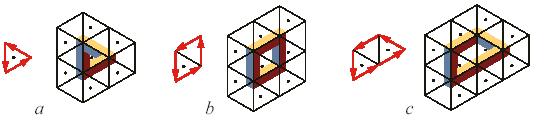
Рис. 9. Три этапа конструирования фигуры.
Начнем, скажем, с плитки с точкой (рис. 9a.). Если эта плитка полностью определяет внутреннюю часть фигуры, то соответствующая фигура (в которой добавлены соответствующие плитки с внешней части пути) является невозможной. Чтобы получить возможную фигуру, необходимо во внутреннюю часть фигуры добавить плитку без точки (рис. 9b). Если добавить еще одну плитку с точкой, то снова получится невозможная фигура (рис. 9с).
Подобное конструирование фигур можно продолжать бесконечно. Таким образом, чтобы получить возможную фигуру, количество плиток с точками и без точек во внутренней части фигуры должны быть одинаковым. Рассмотрим теперь периметры внутренних частей фигур на рис. 9, выражая величину периметра в количестве сторон плиток. Каждый раз, добавляя плитку с точкой к внутренней части фигуры, количество плиток с точками увеличивается на 1, в то время как разница между количеством сторон с точками и без в периметре увеличивается на 3. Более того каждая новая сторона указывает иное направление пространства. Тогда
Td – Tn = (Pd – Pn)/3,
где Td и Tn – общее количество плиток с точками и без точек во внутренней части фигуры соответственно, Pd и Pn – количество сторон плиток с точками и без точек вдоль периметра соответственно, а выражение (Pd – Pn)/3 имеет одно и то же значения для любого из трех направлений пространства. Отсюда следует следующее правило: замкнутая фигура, созданная при помощи данного подмножества, является возможной, если ее внутренняя часть состоит из одинакового количества плиток с точками и без точек. Если количества плиток с точками и без точек различно, то фигура является невозможной, и разница эта остается постоянной, если количество изломов, направленных вниз, у фигуры остается постоянным.
Лестница Пенроузов
В предыдущем разделе фигуры, составленные из плиток, рассматривались, в общем случае, как лестница со ступеньками, расположенными в всех трех основных направлениях пространства. Теперь используем плитки для создания бесконечной лестницы Пенроузов (рис. 10). На рис. 10a показан скелет такой лестницы. Разность между количеством плиток с точками и без точек в данном случае равна 8, соответствует количеству ступенек лестницы. На рис. 10b показан окончательный вид бесконечной лестницы, у которой каждая ступенька получилась расширением соответствующего бруска на рис. 10a.
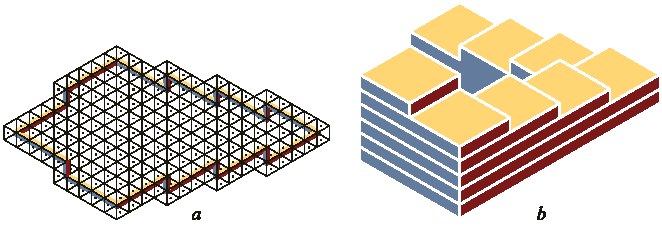
Рис. 10.
a. Скелет невозможной лестницы;
b. Эскиз бесконечной лестницы, созданный на
основе предыдущего рисунка.
Данная лестница подобна той, которую
предложили Пенроузы.
Пересекающиеся бруски
Множество плиток на рис. 11 подобно множеству, представленному на рис. 4, но отличается от него следующими свойствами: 1. Плитки с точками и нефундаментальные плитки исключены из множества; 2. Множество было расширено добавлением плиток, необходимых для построения фигур с пересекающимися брусками на разных уровнях (две группы из шести плиток в правом верхнем углу и правом нижнем). Добавленные во множество плитки имеют закрашенный один угол, соответствующий пересечению двух брусков (группа справа сверху) и стыку брусков (группа справа внизу).
Алгоритм проверки невозможности фигуры, основанный на определении разности между количеством плиток с точками и без точек, может использоваться в данном случае с ограничениями: при помощи данного алгоритма нельзя определить, какой из двух пересекающихся брусков находится сверху, а какой снизу, если они встречаются в одной точке. Более того схема наложения брусков зависит от выбранной точки обзора, тогда как алгоритм от нее не зависит – если вертикальный брусок загораживает горизонтальный при обзоре фигуры спереди, то горизонтальный брусок загородит вертикальный при обзоре фигуры сзади, в то время как стык двух брусков останется стыком с любой точки обзора. Невозможность использования данного алгоритма можно увидеть на рис. 12a: для одного и того же пересечения в верхней части фигуры больше плиток с точкой чем без точки, а в нижней части больше плиток без точки.
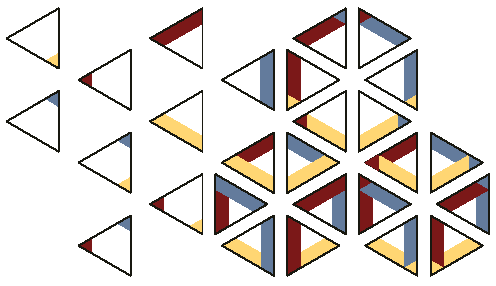
Рис. 11. Множество плиток, позволяющее
создавать невозможные фигуры с
пересечениями. Множество плиток с рис. 4,
если из него убрать точки и повторяющиеся
плитки, является подмножеством данного.
Классический способ проверки наложения двух брусков друг на друга – поместить систему координат в какую-нибудь точку фигуры. Если система координат выбрана так, что положительные направления осей координат направлены на смотрящего (рис. 12.b), то точки с бóльшими значениями координат будут загораживать точки с меньшими значениями координат. На рис. 12.c точка пересечения брусков имеет координату (0, 3, 2) (координаты измеряются в элементах плиток), если она принадлежит вертикальному бруску, и (-2, 1, 0), если принадлежит горизонтальному. Следовательно, вертикальный брусок загораживает собой горизонтальный. Отметим, что это различие в координатах сохраняется в направлении всех осей координат.
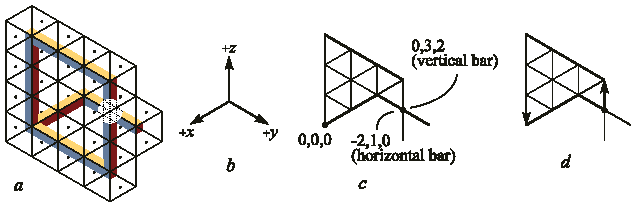
Рис. 12.
a. Алгоритм, основанный на определении
количества плиток с точками и без точек не
позволяет определить, какой из двух
пересекающихся брусков находится впереди,
а какой сзади: в верхней части фигуры
количество плиток с точками больше, чем
количество плиток без точек, в нижней части
фигуры – наоборот.
b. Система координат, положительные
направления осей которой направлены в
сторону смотрящего.
c. Точка с бóльшими координатами
принадлежит бруску, находящемуся спереди.
d. Упрощенный метод. Начиная с точки
пересечения, и следуя вдоль вертикальных
линий, путь идет на 1 плитку вверх и на 3 вниз.
Отрицательное значение (-2) указывает, что
брусок, которому принадлежит исходная
точка закрывает другой.
Результат, полученный, когда фигуры рассматривались в виде лестниц, может быть использован для упрощения метода. Выберите точку, где путь пересекается с самим собой, выберите одну из пересекающихся осей, следуйте вдоль пути, рассматривая только те участки, которые совпадают с выбранным направлением (учитывая знак). Если результат имеет отрицательный знак, то выбранная ось загораживает другую, если знак положительный, то выбранная ось находится позади.
Структура Бельведера М.К. Эшера
Структура на рис. 13 создана при помощи набора плиток, представленного на рис. 11. Отметим, что в данной фигуре сохранена цветовая схема, а в местах пересечения брусков всегда присутствуют плитки, в которых окрашенный угол бруска накладывается на окрашенную сторону. Эта структура представляет интерес, так как она топологически сходна с центральной частью работы М.К. Эшера "Бельведер".
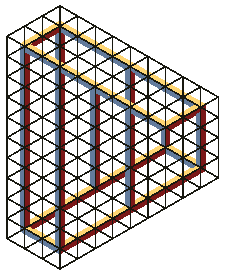
Рис. 13. Фигура, созданная на основе
множества плиток, представленного на рис. 11.
Обратите внимание на перекрывающиеся
бруски: горизонтальные бруски в верхней
части загораживают колонны, которые
находятся, таким образом, и спереди и сзади.
В отличие от других работ М.К. Эшера, в которых использованы невозможные фигуры, – "Водопад" и "Восхождение и спуск" – в работе "Бельведер" мы смотрим на невозможную конструкцию с иной точки зрения. В двух первых работах невозможные конструкции обозреваются а сверху, так как они были представлены в известной статье Пенроузов, в третьей же работе точка обзора находится на том же уровне, что и невозможная фигура.
Выберем точку обзора, согласно Эшеру, так, чтобы уравновесить разницу между левую и правую части фигуры на рис. 13 и изобразим ее в более реалистичной форме (рис. 14). Конечно, мы не можем с уверенностью полагать ни то, что Эшер размышлял именно таким способ при создании "Бельведера", но то, что он вообще рассматривал фигуру подобную рис. 13, а только то, что использование такой точки обзора является достаточным для преобразования этой неуклюжей фигуры в элегантное итальянское палаццо. Работа Пенроузов таких аспектов невозможных фигур не касалась.
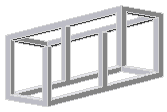
Рис. 14. Фигура с рис. 13, обозреваемая с
точки зрения, находящейся посередине между
верхними и нижними горизонтальными балками.
Данная структура подобна основному
сооружению работы М.К. Эшера "Бельведер".
Фигуры обозреваемые одновременно с двух точек зрения
Еще один тип невозможных фигур, рассматриваемый в данном разделе – это фигуры, обозреваемые одновременно с двух точек зрения. То есть, часть фигуры рассматривается сверху, в то время как остальная часть – снизу. Для получения подходящего набора плиток для создания таких фигур необходимо к множеству плиток на рис. 11 добавить их зеркальные копии (рис. 15). (Плитки с двухсторонней симметрией не добавлялись, так как их отражения подобны исходной плитке)
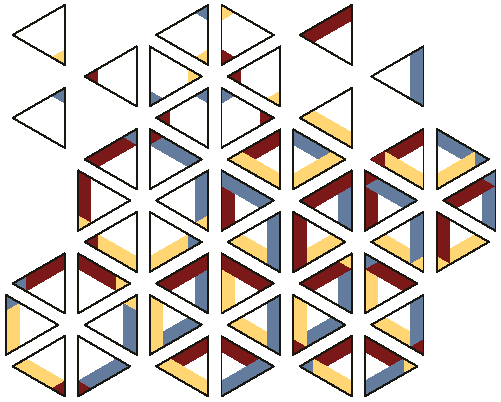
Рис. 15. Множество плиток для создания
фигур обозреваемых с двух точек зрения
одновременно. Таким образом, одна часть
фигуры обозревается сверху, а остальная –
снизу.
Цветовая схема структур, созданных при помощи данного множества плиток, зависит от выбора оси, по которой объединяются две части одной фигуры, обозреваемой с двух сторон. На рис. 16a две части объединяются по вертикальной оси, на рис. 16b – по оси, направленной слева и снизу – вправо и вверх, а фигура 16c – по оси, направленной слева и сверху – вправо и вниз. Во всех трех фигурах цветовая схема для частей, обозреваемых сверху, одинакова, и отличается для частей, обозреваемых снизу.
Когда тип соединения выбран, цвета сторон фигуры в точке соединения частей оказываются определены. В результате бруски, соединяющие две части фигуры направленные в разные стороны, вызывают цветовое противоречие – один брусок, окрашенный по выбранной цветовой схеме в одной части фигуры, может быть окрашен иначе в другой части (см. вертикальные бруски на рис. 16b и 16с).
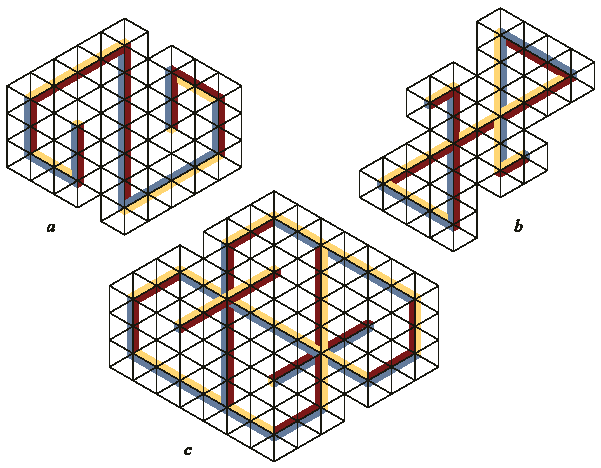
Рис. 16. Цветовая схема части, обозреваемой
снизу, невозможной фигуры с двойственной
точкой обзора зависит от направления
соединения с частью, обозреваемой сверху.
a. Соединением является центральный
вертикальный брусок;
b. Соединением является брусок идущий снизу
и слева – вверх и вправо;
c. Множественное соединение: три
параллельных бруска, следующих сверху и
слева – вниз и вправо.
Использование наборов плиток.
В данном разделе будут представлены некоторые области применения треугольных плиток. В целях сохранения места в дальнейшем будут использованы и нефундаментальные плитки для представления фигур.
Стилизованные невозможные фигуры. Наиболее очевидное использование наборов треугольных плиток – это создание невозможных фигур с желаемыми свойствами. На рис. 17 показан узел, некоторым образом напоминающий узлы Леонардо или кельтские народные орнаменты. Он создан из возможных и невозможных частей, соединенных возможными и невозможными способами.
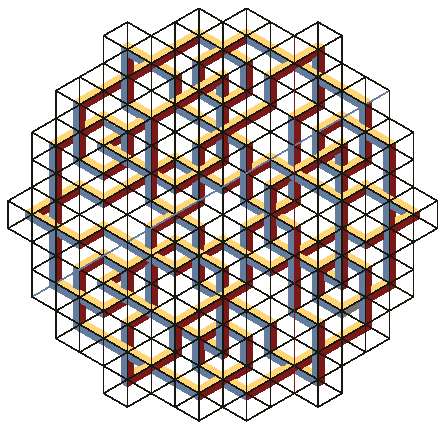
Рис. 17. Узел, созданный при помощи набора
плиток (здесь использовано много
нефундаментальных плиток с целью экономии
места).
Фракталы. Как было сказано в предыдущем разделе, структуры, созданные при помощи множества плиток на рис. 4, без каких-либо потерь определяются путем, проложенным вдоль линий сетки трехмерного пространства, разбитого на одинаковые кубы. Если путь замкнут и не имеет пересечений с самим собой, то он может быть использован для определения регулярного фрактала Коха[7]. На рис. 18a показан исходным многоугольник (треугольник Пенроузов) и, полученный из него, фрактал первого порядка. На рис. 18b показан фрактал четвертого порядка. Обратим внимание, что и исходная фигура и фрактал, полученный из нее, являются невозможными фигурами. Существуют и еще способы построения фракталов, так например фрактал Коха (в некоторых источниках называемый снежинкой Коха), начинаясь с невозможной фигуры, потом может преобразовываться в возможную фигуру на первом шаге.
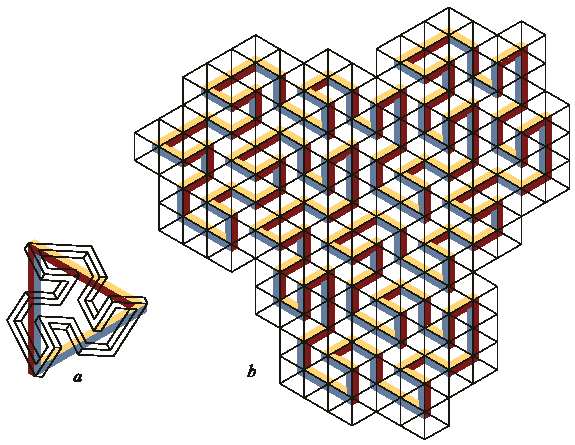
Рис. 18. Регулярный фрактал.
a. Исходный многоугольник (невозможный
треугольник) и фрактал первого порядка;
b. Фрактал четвертого порядка.
Игры (puzzles). Возможно использования плиток в играх, в частности в комбинаторных головоломках. Например, на рис. 19a показан невозможный треугольник. Задача состоит в том, чтобы, используя плитки исходной фигуры, переставить их таким образом, чтобы образовалась возможная структура, сохранив при этом общую форму фигуры (на рисунке показана жирной линией). На рис. 19b показано одно из возможных решений.
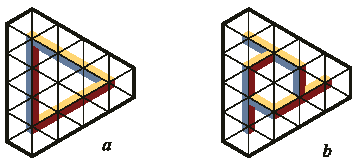
Рис. 19. Комбинаторная головоломка.
а. Необходимо переставить плитки так, чтобы
получилась возможная фигура, сохранив при
этом общую форму фигуры;
b. Одно из возможных решений.
Мозаики. Группа плиток может быть выбрана для формирования фигуры, которой можно замостить плоскость. На рис. 20 выбранная группа плиток из множества на рис. 4 образует такую фигуру. Фигура имеет форму ромба (границы фигуры на рисунке показаны жирными линиями), и при помощи данной фигуры можно заполнить всю плоскость, используя только преобразование смещения. Та же самая группа плиток может быть использована для покрытия плоскости другими способами, некоторые из которых могут включать повороты и отражения.

Рис. 20. Фигура в виде ромба, которой можно
заполнить плоскость, используя
преобразование перемещения.
Помощь в творчестве
Невозможные фигуры являются источником вдохновения многих художников, увлекающих своими парадоксальными работами широкую аудиторию. Люди, интересующиеся невозможными фигурами, но не обладающие достаточными художественными навыками, могут использовать треугольные плитки для создания собственных фигур. С другой стороны, плитки могут служить помощью художникам при создании невозможных фигур, которые потом будут преобразованы в "реально выглядящие" фигуры.
Невозможные фигуры, созданные при помощи множества плиток с рис. 4 имеют две "странные" визуальные характеристики, которые объединяют две различные точки в одну точку на фигуре.

Рис. 21. Два невозможный лестничных пролета.
Базовая структура была создана на основе
множества плиток с рис. 4.
Первая характеристика – это несоответствие расстояний, как это было отмечено в первом разделе. Как выяснили Пенроузы, эта характеристика может быть применена для создания невозможных лестниц. Рассмотрим точку на рис. 21, где пересекаются два лестничных пролета. Следуя по одной лестнице, точка пересечения должна находиться ниже основного уровня, следуя другой – выше.

Рис. 22. Фигура, представляющая собой крайнюю
правую часть фигуры на рис. 13.
Вторая характеристика заключается в том, что невозможные фигуры выглядят странным образом перекрученными. Хотя перекручивание и не является исключительной характеристикой невозможных фигур – множество возможных фигур, составленных из брусков, пересекающихся под прямыми углами, также перекручены, но невозможные фигуры имеют хотя бы один дополнительный оборот, что делает их невозможными. Возьмем фигуру с рис. 13. Отметим, что потолок следует расположен перпендикулярно полу, что получается благодаря невозможным фигурам в левой и правой части конструкции (рис. 22). Если такую фигуру положить параллельными брусками на пол, то она преобразует вертикальную плоскость в горизонтальную. Фигура на рис. 23. художественно иллюстрирует такую трансформацию: вертикальная плоскость (правая часть фигуры с аркой) при помощи невозможной фигуры преобразуется горизонтальную плоскость (шахматную доску). Другие наборы плиток (рис. 11 и рис. 15) обладают своими характеристиками, но могут быть использованы подобными образом.
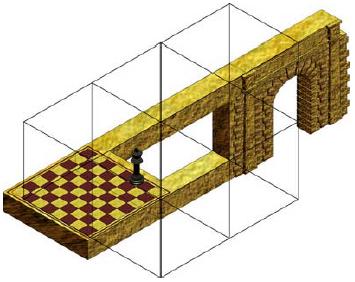
Рис. 23. Художественное представление фигуры
с рис. 22. Вертикальная плоскость
преобразуется в горизонтальную.
О невозможности невозможных фигур
Невозможные фигуры часто называют визуальным парадоксом, однако парадокс лежит, скорее, в системе восприятия человека, нежели в самих невозможных фигурах. Фактически, большинство невозможных фигур являются представлением возможных. Возьмем, к примеру, треугольник Пенроузов. На рис. 24a показана скульптура Мэтью Хамекерса (Mathieu Hamaekers)[1], которая, если не обращать внимания на некоторые тени, выглядит как невозможный треугольник. Но смещая точку обзора, раскрывается природа данной конструкции – треугольник составлен из искривленных частей (рис. 24b). Парадокс заключается в том, что, хотя мы и знаем возможную интерпретацию фигуры, это знание не предотвращает нас от ощущения треугольника Пенроузов как невозможной фигуры.

Рис. 24. Скульптура М. Хамекерса.
a. вид спереди
b. вид под углом 45°.
Психологи полагают, что причина парадокса лежит в правилах восприятия ближнего пространства, полученных в раннем детстве, когда ребенок пытается ощутить пространство, трогая окружающие предметы. Мы воспринимаем окружающий нас трехмерный мир при помощи наших двухмерных сетчаток глаз. В случаях, когда бинокулярное зрение не может нам помочь – например, в случаях, когда объект находится очень далеко от нас – мы теряем возможность видеть стереоизображение, и нам приходится основываться на неясных плоских изображениях. И чтобы понять данные, не являющиеся стереоизображением, мы прибегаем к правилам восприятия пространства.
Одно из основных правил гласит, что мы всегда создаем наиболее стабильную интерпретацию[8]. То есть, если мы переместим немного голову, и, таким образом, немного сместим точку обзора, то интерпретация фигуры, на которую мы смотрим, не изменится.
Это правило объясняет все "невозможные" характеристики в наборах плиток, за исключением набора для фигур с двумя точками обзора. Например, когда бы смотрим на рис. 25a, мы видим, что горизонтальный брусок загораживает вертикальный. И мы не ожидаем, что если мы немного поднимем голову, то обнаружим, что вертикальный брусок имеет разрыв (рис 25b), величина которого в точности совпадает с шириной горизонтального бруска на предыдущем виде.
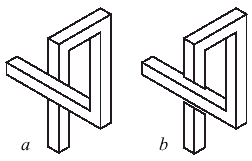
Рис. 25. Мы воспринимаем вид a, как
невозможный, так как не ожидаем, что,
сместив немного голову, увидим вид b.
Как следствие из правила наиболее стабильной интерпретации, мы ожидаем, что если две линии пересекаются в некоторой точке, то пересечение должно сохраниться, если мы немного сместим голову. И еще одно следствие заключается в том, что мы ожидаем, что прямые линию будут оставаться прямыми при некотором смещении. Поэтому мы и не воспринимаем невозможный треугольник и другие невозможные фигуры как скульптуры Хамекерса.
Заключение
Множество невозможных плиток позволяет создать интуитивную связь между различными дисциплинами: дизайн, математика и психология. Показано, что результаты, полученные в одних дисциплинах, могут быть представлены другим. Автор надеется, что множество плиток может быть использовано как инструмент для создания фигур не только уже известных, но и новых. Вы можете сделать себе несколько увеличенных копий наборов плиток и попробовать создавать фигуры самостоятельно. Если вы не желаете заниматься изготовлением плиток, вы можете воспользоваться компьютерной программой Tririles, которая может быть найдена в интернете[9].
Литература и ссылки
- Ernst, B. (1986) Het gegoochelde oog, Landshoff, Utrecht. English translation: Optical Illusions, Taschen, Köln, 1992.
- Escher, M.C . (1967) The Graphic Work of M.C. Escher, Ballantine, New York
- Penrose, L. S. & R. (1958) Impossible Objects: A Special Case of Optical Illusions, British Journal of Psychology, 49, 31-33.
- Other interpretations are also available. For example, in figure 2a the left-hand branch of the horizontal bar can be seen as joining the vertical bar, with the left-hand branch running behind. Although this can easily be handled by drawing lines at the contours of the bars, it will result in a larger number of tiles.
- Uribe, D. (1978) Construcciones imposibles, La Revista del Snark, 8, 9, 10.
- Uribe, D. (1984) Construcciones imposibles, Cacumen, 18, 42-50.
- Mandelbrot, M. (1977) Fractals. Form, Chance and Dimension, W. H. Freeman & Co., San Francisco.
- Hoffman, D. D. (1998) Visual Intelligence, W. W. Norton & Co., New York.
- Tritiles was created by B. Cenk Gazen and M. Burçin Kermen and can be downloaded from www.cs.cmu.edu/~bcg/triangle/triangle.htm or from www.newmedia.kent.edu/eureka/Games/games.htm
Перевод Влада Алексеева
