Виктор Фесенко - Невозможные объекты. Классификация и примеры
НО типа B
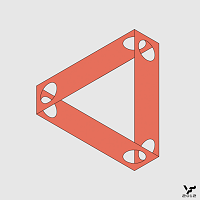
В реальном мире прямолинейная лента из бумаги, закрученная винтом на 90 градусов по типу авиационного пропеллера, не может быть плоской по определению, а для НО типа B это "возможно". Некоторые поверхности или грани НО типа B, позиционируемые как плоские, на своих концах имеют различную угловую ориентацию в пространстве. Смежные плоские поверхности в одной части некоторых НО типа B выглядят как выступающий горб, а в другой его части как внутренние поверхности желоба. Среди НО типа B нет такого яркого и знаменитого "элементарного" представителя, как треугольник Пенроуза и на эту роль может баллотироваться невозможный треугольник, представляющий собой замкнутую ленту:
Отверстия по углам фигуры акцентируют угловую ориентацию участков ленты в углах треугольника и показывают, что все три участка ленты располагаются в трехмерном пространстве, а не лежат в одной плоскости. Дотошные читатели могут возразить, что данная фигура, как и треугольник Пенроуза получена невозможной интеграцией трех элементов, т.е. ее можно причислить к НО типа А. Но полосы между углами фигуры выглядят одновременно и плоскими и закрученными. И это является принципиальным отличием НО типов A и B, дающим право на существование последнего. Указанная невозможная "плоскостность-закрученность" может быть, естественно, применима только для изображенных двухмерных и трехмерных фигур, т.е. среди НО типа A не могут присутствовать одномерные фигуры в виде нитей.
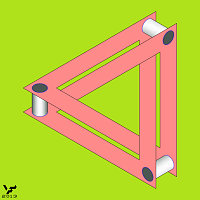
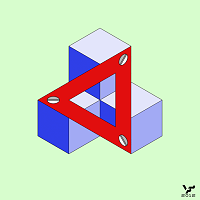
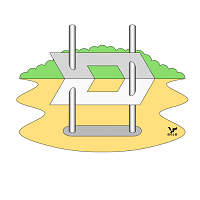
Далее приведены другие примеры двухмерных НО типа B, выполненных в изометрии (Фиг. 066 - 071), последний из которых – Трилистник в виде замкнутой и переплетающейся особым способом ленты известен с давних времен. Но на этом рисунке он является представителем НО типа B:
На Фиг. 072 – 073 изображены также двухмерные НО, но в двухточечной перспективе:
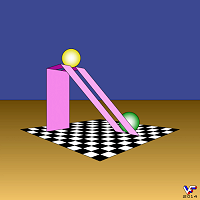
Среди этих геометрически невозможных структур можно отметить одностороннюю замкнутую ленту - аналог ленты Мебиуса, но состоящую из трех плоских участков (Фиг. 074) и абсурдную прямолинейную наклонную направляющую (Фиг. 075), скатываясь по которой, шар незаметно оказывается под ней!
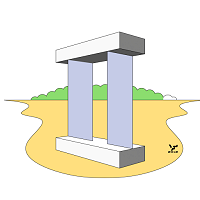
Конфигурация трехмерных НО типа B может быть весьма разнообразной, как показано на Фиг. 076 – 080:
Последний из этих рисунков является логотипом, разработанным автором для пометки своих рисунков НО.
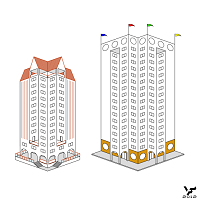
Имея желание еще более увеличить разнообразие НО типа B, автор "построил" несколько невозможных зданий:
Если внимательно рассмотреть эти небоскребы, то выявится дополнительная их невозможность. Внешние контуры небоскребов свидетельствуют о том, что здания позиционируются как построенные в двухточечной перспективе, а верхние и нижние кромки оконных проемов параллельны, как положено в изометрических проекциях. Т. е. небоскребы изображены одновременно и в перспективе и в изометрии. В тоже время здания выглядят вполне естественно, если отдельно рассматривать только их верхние или нижние части.
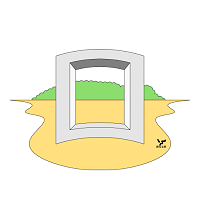
НО типа B могут быть и с криволинейными внешними поверхностями, преимущественно цилиндрическими, и неоднозначная ориентация этих поверхностей проиллюстрирована на Фиг. 084 - 085. Верхняя перемычка неплоской рамки (Фиг. 084), изображенной в двухточечной перспективе, обращена к наблюдателю выпуклой стороной, а нижняя перемычка – вогнутой. Аналогичными невозможными свойствами обладает и кирпич на Фиг. 085.
На Фиг.086 показана еще одна разновидность НО типа B, в которой плоские горизонтальные поверхности культового сооружения незаметно превращаются в цилиндрические стены с вертикальной образующей:
Художниками придумано несколько НО типа B в виде пролетов лестниц или ступенчатых пирамид, в которых вертикальные поверхности уступов между ступенями в одной части фигуры без каких-либо обозначенных переходов превращаются в другой части рисунка в горизонтальные поверхности ступеней. Один из примеров таких НО будет приведен в разделе статьи "Лестницы".