Виктор Фесенко - Невозможные объекты. Классификация и примеры
Невозможные лестницы
Лестницы - одна из наиболее эксплуатируемых художниками разновидностей НО и поэтому автор решил посвятить невозможным лестницам отдельный раздел. Самая первая и самая известная из разнообразного семейства невозможных лестниц – замкнутая в плане лестница на картине М. Эшера "Восхождение и спуск", которая после десятков лет присутствия в различных сюжетах и повторениях уже не вызывает прежних чувств и размышлений. По всем признакам эта лестница относится к НО типа A:
Интересным развитием идеи эшеровской лестницы является замкнутый водяной каскад неизвестного японского художника:
В плане лестница Эшера имеет форму неравностороннего четырехугольника без намеков на какие либо виды симметрии. Автор статьи поставил себе задачу развивать тему невозможных замкнутых лестниц не придумыванием новых сюжетов или обстановки, а поиском ее новых форм с проявлениями большей симметрии и разработкой новых методов их построения. Насколько это удалось, судить читателям.
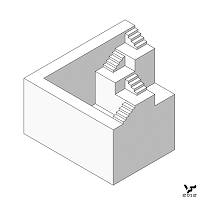
Для рисования невозможных лестниц типа A не требуется особой изобретательности и для этого всего лишь необходимо интегрировать между собой ее самую верхнюю и самую нижние ступени из всей их совокупности. Интегрировать можно непосредственным образом или через промежуточный элемент типа горизонтальной лестничной площадки, как показано на Фиг. 192:
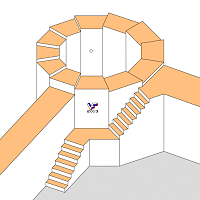
На Фиг. 193 изображена двухпролетная замкнутая лестница на башне с двумя интегрирующими пролеты площадками:
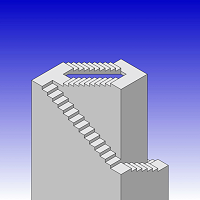
А вот так эшеровская лестница может смотреться сверху в одноточечной перспективе:
Степень ее симметрии явно выше, чем у ее аналога.
Также в одноточечной перспективе изображена двухпролетная невозможная лестница с интегрирующими площадками:
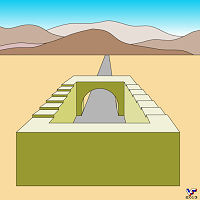
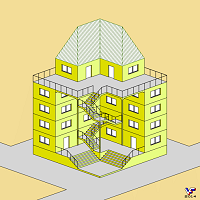
Парадоксальная лестница не обязательно должна быть замкнутой и это показано на Фиг. 196, где для восхождения или спуска, соответствующих одному этажу здания требуется два лестничных пролета. Но на рисунке 6 лестничных пролетов обеспечивают восхождение посетителя на уровень четвертого этажа:
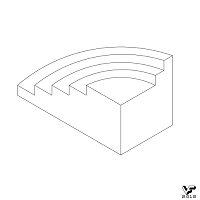
Количество ступеней у замкнутой лестницы может варьироваться в широких пределах, начиная с трех:
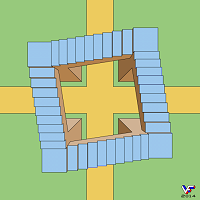
В невозможной замкнутой лестнице не обязательно присутствие соединяющих пролеты площадок, а сама лестница может быть многоугольной в плане:
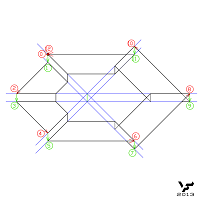
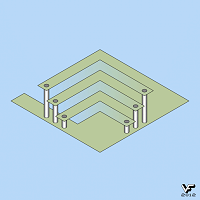
Алгоритм графического построения такой лестницы существенно отличается от способа построения лестницы Эшера и наглядно проиллюстрирован на Фиг. 199:
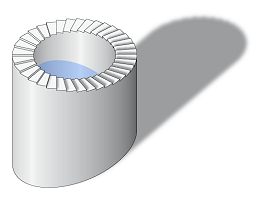
Следует отметить еще одну пока редкую разновидность замкнутых лестниц типа А. На Фиг. XXIII представлена картина художника Эндрю Джадда (Andrew Judd) с круглой в плане замкнутой лестницей, которая построена "на глазок", по этой причине ее ступени больше походят на зубья торцевой кольцевой фрезы с наклонными задними поверхностями:
Другую попытку изобразить аналогичную лестницу с помощью компьютера предпринял художник Gilles Esposito-Farese:
Эффект правдоподобия лестницы увеличен за счет большого количества ступеней и небольшим разворотом вертикальных уступов между ступенями относительно диаметральных плоскостей.
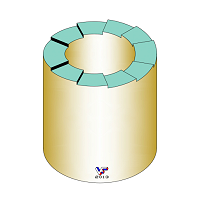
Базируясь на идее двух предыдущих рисунков, автор вознамерился построить более реальное изображение круглой в плане лестницы, у которой окружные кромки всех ее ступеней являлись бы, как и положено в изометрии, участками эллипсов с одинаковым соотношением больших и малых полуосей:
Алгоритм последовательного построения ступеней этой лестницы несколько подобен алгоритму построения многоугольной лестницы на Фиг. 199. Читатели могут заметить некоторую скрытую симметрию изображения относительно горизонтальной оси. Автор при построении попытался обеспечить визуальную одинаковость угловых размеров ступеней в плане, однако это пришлось сделать "на глазок", т.к. пока не представляется, как эту визуальную одинаковость нарисованных в изометрии криволинейных фрагментов выполнить строгими геометрическими построениями. Классическое разделение изображенного в изометрии круга на одинаковые по углам участки при построении замкнутой и круглой в плане лестницы не приводит к приемлемому результату. Ступени даже более простой для построения шестиугольной в плане лестницы на Фиг. 199 визуально неодинаковы и по форме и по размерам. Появившаяся сравнительно недавно такая невозможная однопролетная лестница, как на фотомонтаже Риккардо Баигоррии (Ricardo Baigorria) поражает своими свойствами, а степень ее абсурдности явно выше, чем у лестницы Эшера:
Никакое воображение не позволит представить форму этой лестницы в плане. Если человек, поднимающийся (или спускающийся) по замкнутой лестнице Эшера оказывается на исходной ступени после трех поворотов направо (или налево), что вполне естественно при путешествии по замкнутой прямоугольной траектории, то человек на лестнице Баигоррии оказывается в исходном месте после одного поворота направо и одного поворота налево! Двухпролетную невозможную лестницу с подобными свойствами нарисовал Анатолий Коненко:
Но за самую высокую степень абсурдности может побороться однопролетная лестница, придуманная Джанни Сарконе (Gianni Sarcone) и изображенная на Фиг. XXVII. Двигаясь по ступеням такой лестницы в одном и том же направлении можно и подниматься и спускаться по ней!
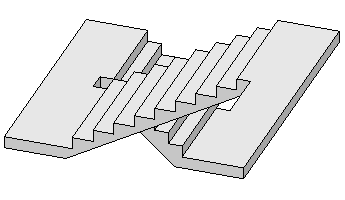
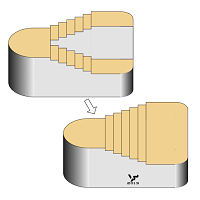
На Фиг. 201 представлена подобная по свойствам однопролетная лестница и ее генезис из возможной (реальной) двухпролетной лестницы:
Дополнительное изящество лестницам, подобным вышеуказанным, могут придать их дугообразные в плане ступени:
На этих двух абсурдных лестницах заканчиваются примеры лестниц, относящихся к НО типа A.
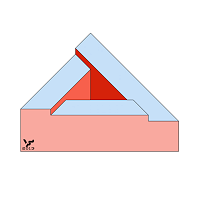
Невозможная лестница на Фиг. 204 по своим геометрическим особенностям подобна культовому сооружению на Фиг. 086 и, следовательно, относится к НО типа B:
Двухкратной степенью парадоксальности по сравнению с лестницей Эшера обладает также замкнутая в плане лестница типа B, изображенная на Фиг. 205:
Лестниц типа B, подобных той, которая изображена на Фиг. 206 придумано немало и объединяет их то, что вертикальные уступы между ступенями в одной зоне рисунка незаметно превращаются в горизонтальные поверхности ступеней в другой:
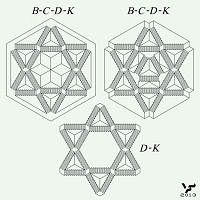
Идея, заложенная в НО на Фиг. 075 получила свое развитие в невозможных лестницах типа B, представленных на Фиг. 207 – 209. Необходимо отметить, что такие лестницы могут присутствовать только на рисунках, выполненных в двухточечной перспективе:
Ступени невозможных лестниц типа Е могут дематериализовываться также, как поверхности и грани чертовой вилки:
На Фиг. 211 по аналогии с кубами Тьерри объединились две круглые башни с внешними винтовыми лестницами. По этой причине эти сросшиеся лестницы следует отнести к НО типа D:
В двухточечной перспективе на Фиг. 212 изображена однопролетная лестница, соединяющая два соприкасающихся мира, не только отличающихся противоположными векторами вертикалей, но и разнесенных друг относительно друга по времени. Так же, как и на Фиг. 186 – 188, материальные структуры – стены башен неуловимо превращаются в нематериальный фон – дневное и ночное небо. Рисунок можно было бы назвать "Лестница времени".
Поливертикальные лестничные экстерьеры различных видов невозможности и их комбинаций представлены на Фиг. 213 и Фиг. 214:
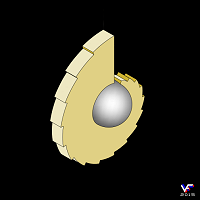
На ранее описанной микропланете с ощутимой силой тяжести можно построить и такую необычную лестницу, как на Фиг. 215:
Такое геометрическое понятие, как "форма в плане" к этой лестнице принципиально не применимо. А поверхности ее ступеней, как отмечалось ранее, должны быть фрагментами концентрических сфер.
После публикации первой части статьи в поле зрения автора случайно попали два рисунка с невозможными лестницами, потребовавшие их обязательного упоминания во второй части:
Первый из рисунков предстал миру на обложке книги Джанни Сарконе (Gianni Sarcone) и Марии-Джо Уэбер (Marie-Jo Waeber) об оптических иллюзиях, вышедшей в 2014 г. Вроде бы реальная при беглом взгляде лестница в башне оказалась вполне достойной для включения ее в разряд самых абсурдных НО. Наше визуальное восприятие окружающего мира постоянно констатирует, что более далекие предметы выглядят более маленькими и поэтому рисование какого либо объекта в классической перспективе требует изображать более далекие его фрагменты меньшими по размерам и ближе к полюсу перспективы. Но на рисунке с обложки книги все иначе - самая верхняя ступень лестницы максимально удалена от расположенного над башней наблюдателя, а поднимающийся по лестнице человек будет относительно стен башни не подниматься, а опускаться! И наоборот, спускаясь по ступеням все ниже и ниже, можно забраться на самый верх башни! Лестница в башне оказалась для автора настоящим сюрпризом, т.к. ее нельзя отнести ни к одному из описанных в статье типов геометрически невозможных объектов. Следовательно, она, по мнению автора, является, возможно, первым представителем невозможных объектов нового типа F, позиционируемых как перспективные изображения, но выполненных с преднамеренными нарушениями основополагающих принципов перспективного построения.
Четырехбашенное строение на Фиг. XXIX, придуманное художником Сандро дель-Пре (Sandro Del-Prete) по пространственному парадоксу подобно лестнице Эшера. Вот только парадокс эшеровской лестницы «измеряется» пятнадцатью ступенями, а на этом рисунке - суммарной высотой четырех больших башен. Прием, использованный Сандро дель-Пре для обеспечения замкнутой траектории путешествия по всем четырем башням существенно отличается от примененного Эшером и заключается в целенаправленном нарушении правил построения изображения в одноточечной перспективе. Вместо одного полюса (точки схода) вертикальных линий, художник использовал четыре точки и, к тому же, искривил вертикальные стены и углы башен для обеспечения их абсурдной интеграции друг с другом. Это четырехбашенное сооружение характеризуется несколькими причинами своей невозможности и, следовательно, является НО гибридного типа.
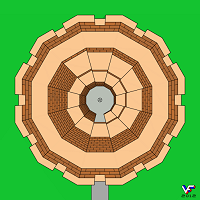
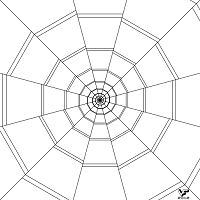
Описание вариантов невозможных лестниц заканчивается на бесконечной винтовой лестнице, изображенной на Фиг. 217. А для того, чтобы оперативно разобраться в ее конфигурации, служит предыдущий рисунок (Фиг. 216), на котором просматривается в плане круглая кирпичная башня с внутренней винтовой лестницей. Невозможность бесконечной винтовой лестницы и не пространственная и не геометрическая. Высота ее превышает поперечник нашей вселенной в бесконечное число раз, невозможны такие силы гравитации, которые она позволяет преодолевать при восхождении. Нарисовать такую лестницу целиком принципиально невозможно, т.к. у лестницы нет ни начала, ни конца, в ней бесконечное количество ступеней, можно довольствоваться только приближенным изображением ее половины. Проекция бесконечной винтовой лестницы на плоскость рисунка представляет собой спиралевидную фрактальную фигуру.