Cameron Browne. Impossible fractals
3. Triangular fractals
Figure 1 (middle and right) shows two well-known fractal developments of the triangle, the Koch snowflake and the Sierpinski gasket. The snowflake modifies the triangle's perimeter shape while the gasket recursively subdivides its interior.
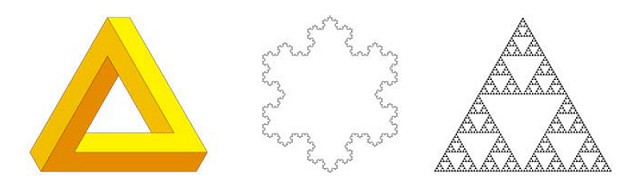
Figure 2 illustrates a development of the tri-bar as an impossible snowflake. The first iteration can be constructed entirely from a single subshape, the acute generator (top right), repeated six times in a cycle with appropriate colouring. Further iterations require a combination of acute and obtuse generators.

Figure 3 shows an alternative snowflake development that retains parent triangles from previous generations and uses them as a framework upon which subsequent triangular struts are added. Although this is not a traditional snowflake and the final design is busier than the previous figure, this approach only requires a single generator (right) and the struts enhance the ambiguity of perspective to give a stronger effect.

In both cases, the thickness of all bars in the figure are uniformly reduced with each iteration to retain the shape's definition. Unfortunately, the illusion's effect diminishes with each iteration as the subshapes become harder to distinguish.
Turning now to the Sierpinski gasket, Figure 4 shows how a gasket-like impossible object may be developed by successive replication of the tri-bar at smaller scales. Note that each of the tri-bar's three bars has an internal and external face, and that each subtriangle must match colours with the parent's faces to which it joins. This is straightforward for the first iteration in which the subtriangle joins the outer faces of the parent triangle (left), and for the second iteration in which each subtriangle joins the inner faces of its parent (middle), but becomes problematic for further iterations which require subtriangles to join two inner and one outer face (or vice versa) if consistent colouring is to be maintained. This problem does not occur with the figure's central subtriangle (right) which remains consistently coloured for any number of iterations, however this is not a standard gasket recursion.

