Cameron Browne. Impossible fractals
8. Pythagorean trees
The multibar fractals considered so far have involved bars of uniform thickness (if not uniform length) at each level of recursion. We now consider a multibar design with bars of continuously decreasing thickness between levels that more precisely matches its fractal equivalent.
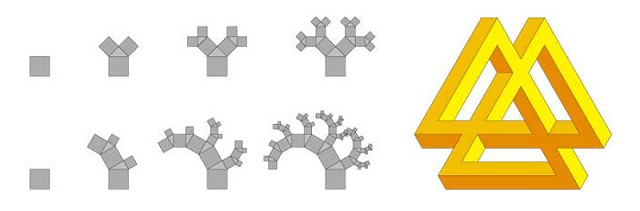
Figure 13 (top left) shows the first four iterations of a 45° Pythagorean tree, which is a structure composed of squares such that the three touching squares at each branch form a 45° right triangle. Figure 13 (bottom left) shows the first four iterations of a balanced 30° Pythagorean tree. This tree is described as "balanced" because the left branching squares, which are almost twice the size of the right branching squares, grow twice each iteration, forcing greater development in the more visible parts and resulting in a more homogenous spread of detail. A traditional 30° Pythagorean tree would require almost twice as many iterations to achieve a similar look, hence the balanced tree allows significant computational savings. The 45° Pythagorean tree is balanced by default.

Figure 13 (right) shows an extended tri-bar from Penrose and Penrose's 1958 article [2] that suggests a method for handling branches and adapting a multibar motif to the Pythagorean tree. Figure 14 shows the extended tri-bar adapted to a 45° Pythagorean tree after fifteen iterations, and Figure 15 shows it adapted to a balanced 30° Pythagorean tree after ten iterations. Note that the perceptual effect remains evident for several iterations, until the bars become too fine to distinguish.

