Trefoil knot
 Trefoil knot |
In knot theory, the trefoil knot is the simplest nontrivial knot. It can be obtained by joining the loose ends of an overhand knot. A trefoil knot is the unique prime knot with three crossings.
Mathematically, it can be described in many variants.
History
The symbol of the trefoil knot has known from ancient times as triquetra. Triquetra is a work derived from Latin tri- (three) and quetrus (cornered). Its original meaning was simply "triangle" and it has been used to refer to various three-cornered shapes.
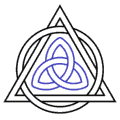 Triquetra in blue as part of an interlaced Christian Trinitarian decorative symbol. |
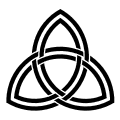 An interlaced double Triquetra. |
 Triquetra interlaced with circle as Christian Trinitarian symbol (a "Trinity knot"). |
The triquetra has been found on rune stones in Northern Europe and on early Germanic coins. (See also images of Borromean rings on rune stones)
 Triquetra on one of the Funbo Runestones, located in the park of Uppsala university. |
Also, the triquetra is often found in Celtic art. While it is uncertain what the symbol may have meant to the Celts, it is often found as a design element in larger drawings of triskeles or triple spirals. Later, the symbol was used by Christians as a symbol of the Trinity (Father, Son and Holy Spirit).
Nowadays, the triquetra has been used in various logos. A triquetra is one of the four symbols on the cover of the Led Zeppelin album, "Led Zeppelin IV", where it used as the personal symbol of bassist John Paul Jones.
Art
Trefoil knots has frequently used in art. Dutch artist M.C. Escher shown three versions of the knot on his lithograph "Knots". On of them is a kind of Möbius strip.
 Knots M.C. Escher |
There's sculpture of the trefoil knot the Hollander York Gallery, on Toronto's Yorkville Avenue.
 Trefoil knot near Hollander York Gallery |
Derived variations
Trefoil knot can be easely transformed into Möbius strip as you can see on the photo of sculpture by Carlo H. Séequin.
 Double trefoil knot by Carlo H. Séequin |
The smooth shape of the trefoil knot can be transormed into the figure with straight lines and formed into impossible figure like Penrose tribar.
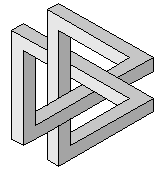 Impossible trefoil knot |
Appendix. Artistic examples of the trefoil knot
 Möbius-Trefoil Knot Gears by Tom Longtin |
