Приключения с невозможными фигурами
10. Проверка на невозможность?
Если мы нарисуем фигуру, которая на самом деле не может существовать в пространстве, будет ли это очевидно? Есть ли простой тест, который бы достоверно сказал нам, что конкретная фигура является возможной или нет?
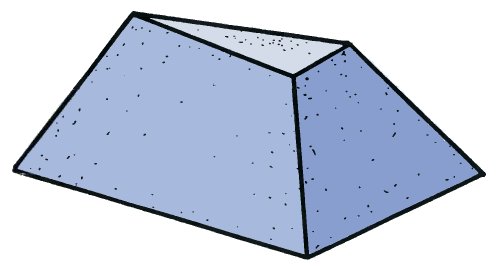
Большинство людей воспринимают данный рисунок как реальную усеченную пирамиду. Тем не менее, я могу сказать, что это настоящая невозможная фигура и могут доказать это. Вы видите, почему она невозможна? Объяснение представлено на странице 94, но попробуйте найти решение самостоятельно.
Для того, чтобы принять решение о том, как выглядит фигура, мы не можем опираться только на автоматическое восприятие зрением. Нам необходимо обдумать, чтобы провести рассуждения и попытаться найти методику или тест, который поможет нам принять правильное решение.
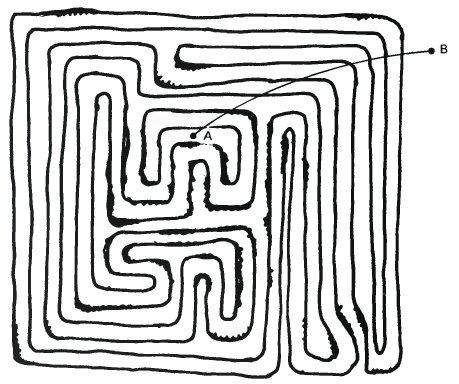
Рисунок выше не является невозможной фигурой, но он демонстрирует, как автоматическое восприятие зрением стопорится, когда изображение становится слишком сложным. Фигура состоит из одной длиной и узкой петли завернутой подобно кишечнику. Проблема заключается том, чтобы решить находится ли точка A внутри или снаружи петли.
Чтобы решить эту проблему мы должно сделать больше, чем просто взглянуть на изображение. Нам необходимо подумать. Один из способов решения – это отнестись к ней как к проблеме выхода из лабиринта. Если мы не сможем найти выхода наружу, тогда можно будет сказать, что точка A лежит внутри петли. Однако у большинства из нас были проблемы с решением головоломок с лабиринтами, и навсегда останется сомнение, что остались какие-то еще не открытые пути, которые могут вывести наружу.
Для решения этой проблемы существует лучшее решение. Нарисуем любую линию, прямую или кривую, он точки A наружу. Например, отрезок AB на рисунке выше. Теперь давайте посчитаем количество линий, которые пересек отрезок. Каждый раз, когда мы пересекаем линию, мы либо переходим с внутренней стороны на наружную или с наружной на внутреннюю. Четное количество пересечений на пути к выходу будет означать, что точка A находится снаружи петли. Нечетное количество будет означать, что точка A – внутри. При помощи этого простого теста очень просто сделать правильное заключение.
Данная проблема была выбрана из-за того, что у нее имеется несколько путей решения с разной степенью достоверности. Может быть, мы могли бы использовать такие же идеи для разработки теста для применения к невозможным фигурам?
Многие пытались разработать простой тест, подобный приведенному на предыдущей странице, но пока без полного успеха. Некоторые тесты применимы только для определенных фигур наподобие трибару, четырехбалочнику или мультибарам.
Возможно, вы захотите поэкспериментировать со следующим тестом.
Нарисуйте или представьте сечение фигуры плоскостью. Линия на каждом из следующих рисунков является плоскостью, хотя плоскость не обязательно должна быть перпендикулярна листу бумаги. Закройте часть фигуры с одной стороны линии листом бумаги. Теперь нарисуйте рисунок сечения, которое формирует плоскость на оставшейся части фигуры. Затем закройте фигуру по другую сторону от линии сечения.
Если оба наброска одинаковы, тогда фигура возможна. Если они отличаются хоть в чем-то, тогда фигура невозможна.
Чтобы проиллюстрировать работу данного метода, ниже приведены пять примеров. Четыре из них – невозможные фигуры, и одна – возможная.
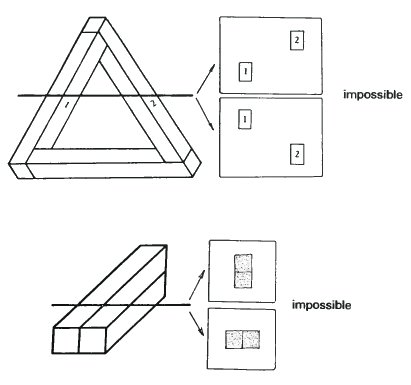
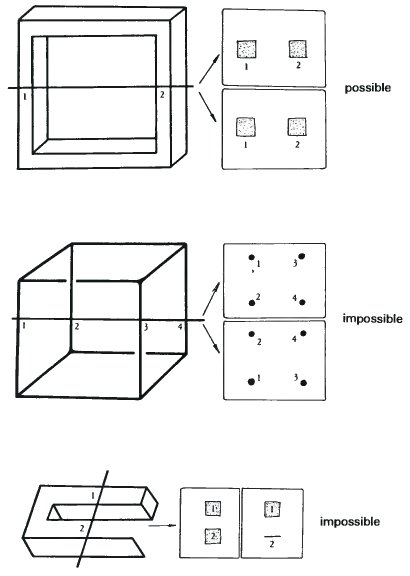
Данный метод все равно требует хорошего понимания тестируемой фигуры, в котором присутствует доля субъективного суждения. Он не очень хорошо работает для фигур подобных пирамиде со страницы 90, где невозможность не так ярко выражена. Но я надеюсь, он укажет направление, где в один прекрасный день будет найдено решение этой сложной проблемы.
Нечто уникальное
Изучение невозможных фигур добавило нечто новое и уникальное к визуальному миру человека. Оно предлагает обогащение человеческого духа и широкое поле для исследования человеческого воображения. Конечно, это не область математики, хотя математические методы могут быть использованы для описания и анализа фигур. Но это и не обязательно искусство. Невозможные фигуры могут быть изображены гармонично и выразительно, но они также могут быть и уродливы. Они пробуждают отклик у большинства людей, некоторое ощущение чуда, и они, безусловно, помогут нам понять, как наши глаза и мозг обрабатывают зрительную информацию. Понимание этого поможет в разработке программ, которые позволят компьютеру управляющему роботами "видеть". Возможно, не будет удивительным тот факт, что из более чем 100 статей о невозможных фигурах, написанных с 1970 года (прим. переводчика, имеется в виду количество статей, опубликованных до даты выхода данной книги в 1985 году), подавляющая часть опубликована к компьютерных журналах.
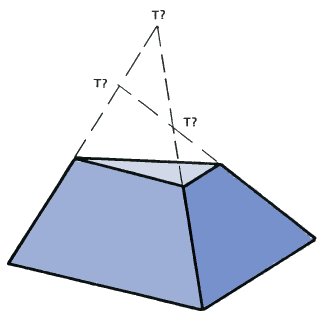
Решение задачи со страницы 90.
Продолжения трех линий боковых ребер пирамиды приводит к трем разным точкам пересечения, каждая из которых должна быть вершиной пирамиды. Следовательно, это невозможная фигура.
