Наследие Эшера. К столетию со дня рождения
Компьютерные игры, основанные на пространственных иллюзиях Эшера
Мне всегда нравилось, как Эшер приглашает окунуться в свои миры. В "Восхождении и спуске" Эшер предлагает присоединиться к процессии монахов, идущих по бесконечной лестнице. В "Выпуклости и вогнутости" он просит сравнить объекты в левой части с их перевернутыми двойниками в правой. Его регулярные разбиения плоскости заставляют отслеживать двойную логику кривых, очерчивающих плитки.
Эшер однажны сказал, что если бы у него была бы вторая жизнь, то он хотел бы стать аниматором. Возможно, в третьей жизни он бы захотел заняться разработкой игр.
Многие художники считают, что игры позволяют зрителям почувствовать их работы гораздо глубже. Итальянский скульптор Мигель Беррокаль (Miguel Berrocal) создает замысловатые скульптуры, которые распадаются на много частей. Японский художник Тосио Иваи (Toshio Iwai) сделал компьютерную игру под названием SimTunes, которая предлагает пользователям экспериментировать с образцами цвета и звука. Когда я играю со скульптурой Беррокаля или в игру Иваи, я получаю практическое понимание того, как отдельные части связаны друг с другом. Этот опыт сильно отличается от того, как если бы я пассивно рассматривал их. "Я слышу и забываю, я вижу и запоминаю, я делаю и я понимаю."
Escher Interactive
Мне выпал шанс участвовать в разработке эшеровской игры в 1994 году, когда автор игры Йост Элферс (Joost Elfers) предложил мне сотруднического в разработке CD-ROM под названием Escher Interactive. Весь следующий год вместе с программистами Девидом Остером (David Oster) из Калифорнии, а также Майком Чановски (Mike Chanowski) и Хенком Аллесом (Henk Alles) из компании Eyeware Interactive в Недерналдах, где собственно и производился диск, создав коллекцию из шестнадцати "невозможных головоломок". Они называются невозможными не потому, что их невозможно разгадать, а потому что они основаны на невозможных фигурах и других пространственных иллюзиях из работ Эшера.

Escher Interactive стала первым большим программным проектом, основанным на работах Эшера. Диск, выпущенный в 1996 году, содержал галерею работ, хронологию, интервью с экспертами, анимации работ Эшера, три игры и графических редактор для создания регулярных разбиений плоскости (см. рис. 1).
Невозможные головоломки
Цель каждой "невозможной головоломки" заключается в составлении заданной фигуры из набора частей. Чаще всего финальная фигура является оптической иллюзией. Каждая часть составлена из кубов, изображенных в изометрической проекции. Части можно накладывать друг на друга, но не поворачивать.

Первые восемь головоломок - это восемь букв имени Эшера (M.C. ESCHER). Остальные восемь основаны на некоторых работах Эшера. Каждая головоломка имеет уникальное решение, чтобы сделать их сложнее, а также, чтобы облегчить компьютеру проверку решения. Все шестнадцать головоломок показаны на рис. 2.
Идея невозможных головоломок впервые появилась в моей предыдущей игре Heaven & Earth [10]. Я придумал более шестисот головоломок на тему иллюзий для игры Heaven & Earth, работая вместе с ведущим разработчиком Майклом Файнбергом (Michael Feinberg), продюсером Бредом Фреггером (Brad Fregger), программистами Яном Гилманом (Ian Gilman) и Майклом Сендижем (Michael Sandige), художником Марком Феррари (Mark Ferrari) и музыкантом Ричардом Мариоттом (Richard Marriott).
M.C.
Первые две головоломки M и C показаны на рис. 3. Цель - перекрыть маленькие части так, чтобы получилась копия большой фигуры. Элементы нельзя вращать, то есть они должны остаться в исходной ориентации. Конечно вы можете играть в эту игру с вырезаннами кусками бумаги, но на компьютере элементами гораздо проще манипулировать. Элементы автоматически становятся на место и выдвигаются на верхний план, когда вы кликаете по ним мышкой. И компьютер автоматически соблюдает правило, что элементы не должны поворачиваться.
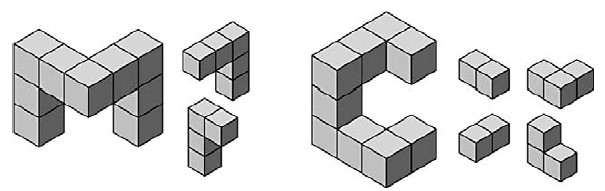
Как и в большинстве компьютерных игр, первые несколько головоломок решаются просто, а затем постепенно становятся сложнее и сложнее. Основное назначение первых двух головоломок обучить правилам игры. На рис. 4 показаны решения первых двух головоломок. Обратите внимание, как элементы перекрывают друг друга.
ES
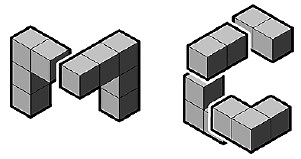
Головоломки E и S показаны на рис. 5. Хотя элементы выглядят объемными, игрок должен думать, что это плоские куски бумаги. Элементы иногда перекрываются так, что не появляется ощущения трехмерного пространства. Последовательность решения для головоломки E показана на рис. 6.
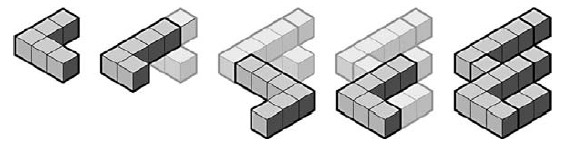
CH
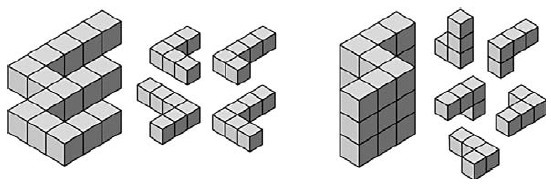
Головоломки C и H представлены на рис. 7. Заметим, что наше представление форм в трех измерения смещается по мере совмещения элементов друг с другом. Например, в последовательности решения головоломки C кубы, которые выглядят принадлежащими одной плоскости на одном этапе смещаются на разные плоскости на следующем этапе из-за добавление новых элементов.
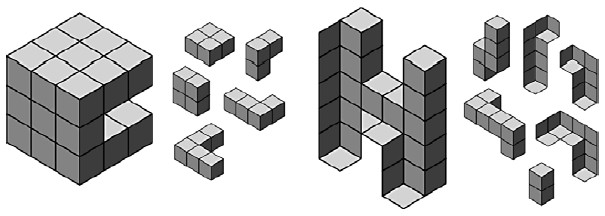
Мне попадались другие иллюзии, в которых наше восприятие ситуации смещается при добавлении или удалении элементов, но я не знаю почему никто не дал названия этому виду иллюзий. Я бы назвал их "интерактивными иллюзиями". Так как интерактивные иллюзии управляются вами, их эффект особенно удивителен. (Я использовал интерактивные иллюзии в нескольких моих компьютерных играх. Например, в игре "Heaven & Earth" присутствуют интерактивные иллюзии, основанные на двусмыленном восприятии фигуры и фона.)
Головоломка H знакомит нас с неоднозначностью выпуклости и вогнутости, как в литографии Эшера "Выпуклость и вогнутость". Сборка этой головоломки приводит к некоторой дезориентации. Элементы часто перекрываются сторонами с противоречивыми интерпретациями. Для, в частности, достаточно трудно найти способ разбить эту фигуру на элементы. Так что решение этой головоломки уникально.
ER
Последние две головоломки, образующие фамилию Эшера, представлены на рис. 8. Вторая буква E - "невероятная фигура". Она выглядит как буква E только под определенным углом. Заметим, что форма буквы составлена от L тетрамино различных ориентаций. Чтобы решение головоломки было уникальным, в наборе нет ни одного одинакового элемента.
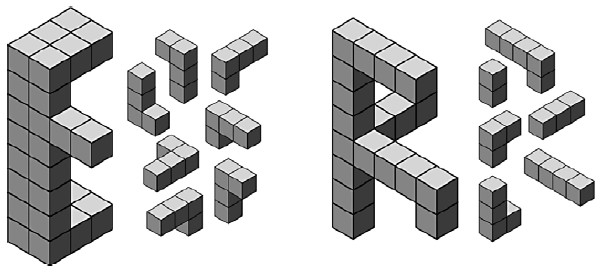
Головоломка R - невозможная фигура подобная невозможному треугольнику, который изображен на картина Эшера "Водопад". Чтобы усложнить задачу я сделал начальную расстановку элементов такой, чтобы она выглядела близкой к решению. На самом деле почти все элементы стоят не на своих местах.
Эшер изредка использовал зрительные трюки с формами букв. На рис. 9 показана литография, которую он сделал для анонса выставки четырех художников. Заметим, что одни и те же символы воспринимаются по-разному в зависимости от их ориентации. Буква E также является и буквой M, буква H - как I, U - как C и т.д. Подобный дизайн кроссворда изображен в начале и конце эпического свитка Эшера "Метаморфозы".
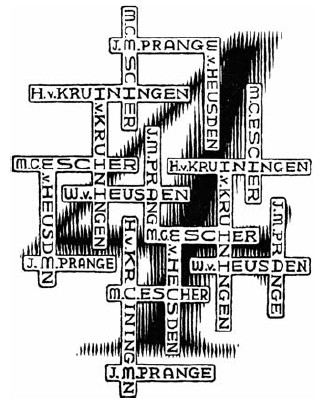
Аналогичный дизайн имени "M.C. Escher" изображен в моей книге об иллюзорных текстовых
изображений - инверсий. Анимация данного дизайна появляется в "Escher Interactive".
Треугольники
Невозможный треугольник, также известный как Трибар Пенроуза, был открыт британским психологом Лайонелом Пенроузом и его сыном физиком Роджером Пенроузом в 1958 году. (Шведский художник Оскар Реутерсварда открыл эту фигуру гораздо раньше, но он не публиковал своих работ до последнего времени). Их статья [9], которую они отправили Эшеру, включала изображения невозможного треугольника и бесконечной лестницы.
Головоломки "Невозможный треугольник" и "Относительность" показаны на рис. 10. Попробуйте поиграть с демо-версией головоломки невозможного треугольника с CD-ROM, который идет с данной книгой. Когда вы соедините один брусок с другим, вы обнаружите, что цикл всегда замыкается, и один из брусков расположен перед другим, хотя должен быть позади. Используйте два дополнительных параллелограмма, чтобы исправить этот дефект.
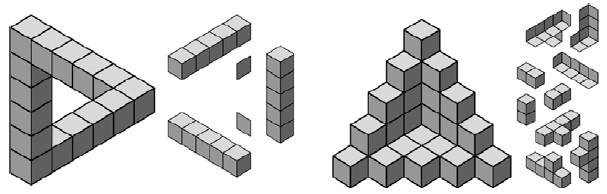
Литография Эшера "Относительность" также включает треугольник, но не невозможный. Вместо этого, данная работа играет с двусмысленностью, какая сторона является верхней. Соответствующая головоломка упрощает треугольник лестниц с литографии Эшера и добавляет новый поворот. Ее элементы полностью меняюся с выпуклых на вогнутые подобно картине Эшера "Выпуклость и вогнутость".
Плоское и объемное
В литографиях "Дракон" (рис. 11) и "Две дорические колонны" Эшер задает вопрос, когда изображение выглядит плоским или объемным. Что превратить эти работы в головоломки, я должен был найти способ упростить изображения до параллелограммов. В каждом из случаев мне пришлось пойти на определенные компромиссы (рис. 12).

Головоломка "Дракон" сохраняет эффект согнутых отрезов листа бумаги, но исключает самого дракона. Головоломка "Колонны" использует иллюзию несколько отличающуюся от иллюзии в оригинальной картине. Вместо противопоставления плоского и объемного здесь эксплуатируется противопоставление выпуклого и вогнутого. Тем не менее она сохранила две колонны, каждая из которых опирается на противоположный конец другой колонны. Эта иллюзия поразительным способом отмечена в картина Сандро дель Прете и Жоса де Мея.
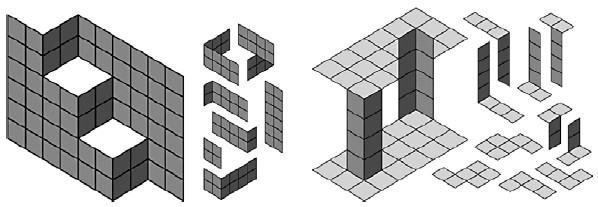
Заметим также, что колонны в варианте Эшера и в моем - симметричны. Но одна из пар элементов головоломки "Колонны" не симметрична.
Лестницы
Картина Эшера "Выпуклость и вогнутость" - классическая иллюзия двусмысленной лестницы, разбитую на симметричный набор элементов. Соответствующая головоломка также содержит пары симметричных элементов (рис. 13). Картина Эшера "Восхождение и спуск" содержит невозможную бесконечно поднимающуюся лестницу. Соответствующая головоломка сокращает лестницу до одной ступеньки на каждом пролете. Если мы еще сильнее сократим лестницу, то получим невозможную лестницу с наименьшим количеством ступенек, составленную из кубов (рис. 14).
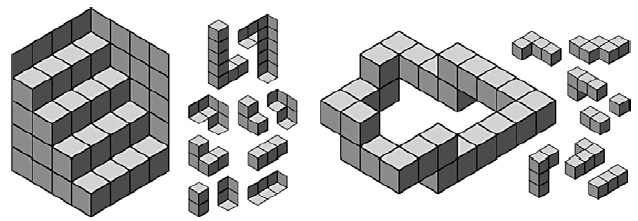
Конечно, бесконечно поднимающаяся лестница невозможна только, если мы предположим, что кажущиеся нам прямые линии, прямые углы и стыкующиеся друг с другом куба действительно такие, как выглядят на рисунке. Если мы предположим, что кубы быть немного искаженными с волнистыми поверхностями, тогда мы сможем сделать трехмерную модель, которая выглядит точно как исходная фигура, но только с одного угла обзора.

Обратите внимание, что и в оригинальной работа Эшера и в моей головоломке два левых лестничных пролета короче, чем два правых. Эта асимметрия эстетически непривлекальна, но неизбежна. В моем исследовании четырехмерных невозможных фигур, то есть о трехмерных "рисунках", которые выглядят невозможными для четырехмерного зрителя, я обнаружил четырехмерный аналог невозможной лестнице, у которого нет этой асимметрии.
Невозможные фигуры
Последние две головоломки содержат невозможные фигуры. Спуск воды в картине Эшера "Водопад" составлен из трех невозможных треугольников. Соответствующая головоломка делает геометрию этого объекта более абстрактным (рис. 15). Обратите внимание, что края элементов головоломки окрашены по-разному.
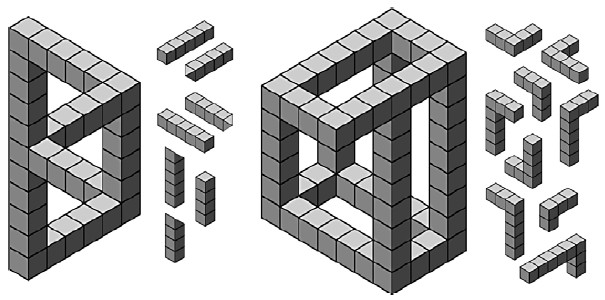
Сидящий человек с виньетки Эшера "Человек с кубоидом" (рис. 16) такой же, как и человек, сидящий у основания лестницы на литографии "Бельведер". Он держит в руках модель подобную фигуры из головоломки "Бельведер" (рис. 15). Так как точная модель предмета, который он держит, уже появлялась в "Heaven & Earth", для "Escher Interactive" я закрутил ее немного по-другому.

Заметим, что у "куба" есть две точки, в которых один брусок пересекает другой. Поскольку швы кубов видимы задний брусок может выгдять сливающимся с передним брусков в этих точках. Я эксплуатирую эту двусмысленность в решении (рис. 17).

Попробуйте сами
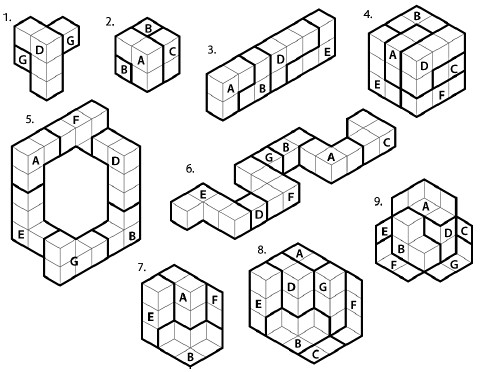
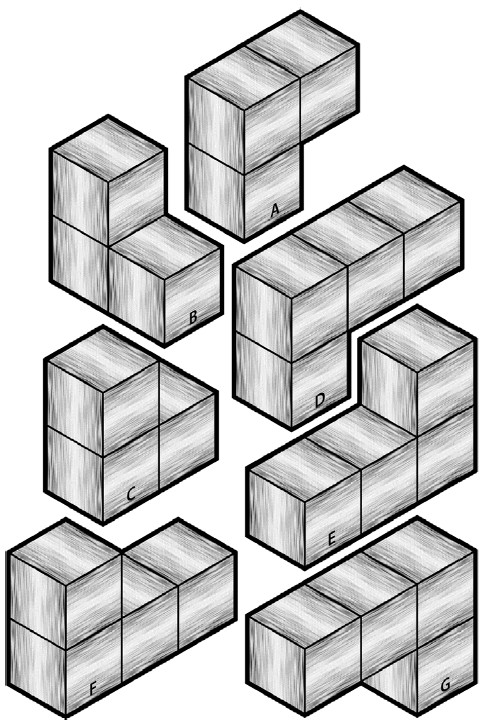
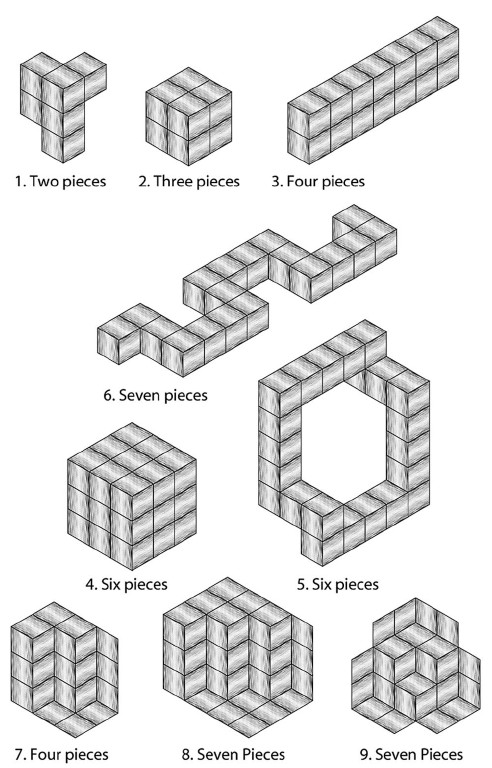
Ниже представлены невозможные головоломки, с которыми вы можете поиграть без компьютера. Изначально они были опубликованы в журнале Games Magazine. Перенесите рис. 18 на плотную бумаги и разрежьте на части. Совместите элементы головоломки для получения разнообразных фигур с рис. 19. Вы можете вращать и накладывать элементы друг на друга, но не можете гнуть или обрезать их. В каждой головоломке указано, сколько элементов вы можете использовать. Решения головоломок приведены ниже.
Литература
- Ernst, Bruno, Adventures with Impossible Figures. Berlin: Taschen 1985.
- Eyeware Interactive BV, Escher Interactive: Exploring the Art of the Infinite (CDROM for Windows). New York: Harry N. Abrams, London: Thames & Hudson, Paris: Hachette Multimedia, Cologne: Dumont Verlag, Utrecht: A. W. Bruna, 1996.
- Gardner, Martin, "From Burrs to Berrocal", Scientific American, January 1978. Reprinted in Penrose Tiles to Trapdoor Ciphers, W. H. Freeman and Company, 1989.
- Iwai, Toshio, SimTunes (CD-ROM for Windows). Electronic Arts / Maxis, 1996.
- Kim, Scott, "An Impossible Four-Dimensional Illusion". In Brisson, David. Hypergraphics: Visualizing Complex Relationships in Art, Science and Technology. Westview Press, 1978.
- Kim, Scott, "Convex Concave", Games Magazine, October 1993, p. 20.
- Kim, Scott, Inversions: A Catalog of Calligraphic Cartwheels. Key Curriculum Press, 1996.
- Kim, Scott, www.scottkim.com
- Penrose, L. S., and Penrose, R., "Impossible Objects: A special type of illusion", British Journal of Psychology [49] (1958), 31.
- Publishing International, Heaven & Earth (floppy disks for Mac or Windows). Buena Vista Software, 1992. (out of print)