Статья из журнала "Квант"
"Невозможные" фигуры
Калейдоскоп журнала "Квант"
В 1934 году из-под кисти шведского художника Оскара Реутерсварда (Oscar Reutersvärd) вышло полотно, положившее начало новому направлению современного искусства с названием imp-art (от английских слов impossible - невозможный и art - искусство). В центре его внимания стало тонкое обыгрывание геометрических мотивов. Копия картины Реутерсварда изображена на рисунке 1. Присмотритесь внимательно: возможно ли такое расположение девяти кубов в пространстве?
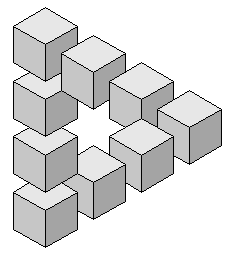
Рисунок 1.
Впоследствии Реутерсвард придумал около 2500 подобных сюжетов, изображающих необычное, парадоксальное, иллюзорное отображение трехмерного мира на двумерный холст картины. В частности, в одном из своих сюжетов число кубов он довел до минимально возможного количества: трех (рис. 2).
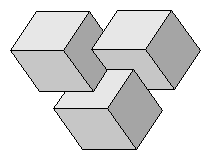
Рисунок 2.
В 1954 году независимо от Реутерсварда английский математик и физик Роджер Пенроуз придумал объект, названный им "Невозможный треугольник" (рис. 3). Если Реутерсвард все свои фигуры рисовал в изометрической проекции, которую он называл "японской", то в исходном треугольнике Пенроуза присутствовал некий эффект перспективы (ребра по каждой из трех сторон не были параллельны друг другу). Это еще более усиливает ощущение невозможности.
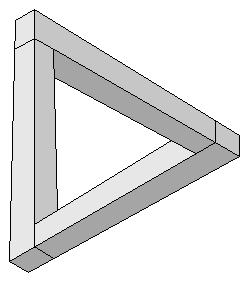
Рисунок 3.
Дальнейшие модификации "треугольника" Пенроуза в сторону увеличения количества "сторон" показаны на рисунке 4.
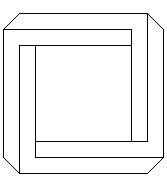
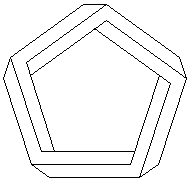
Рисунок 4.
Значительный вклад в искусство парадоксальных эффектов внесли художники Мауриц К. Эшер, Жос де Мей, Сандро дель Пре, Иштван Орос, Висенте Мевилла Сегуи и другие. Их работы вызывают интерес не только у ценителей искусства, но и у математиков и психологов.
Вот еще несколько ярких образцов из обширной и постоянно пополняющейся коллекции "невозможных" фигур (рис. 5-7).
Оскар Реутерсвард
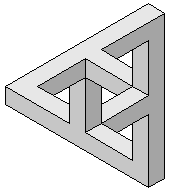
Рисунок 5.
Влад Алексеев
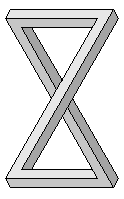
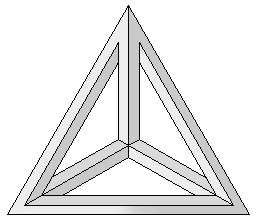
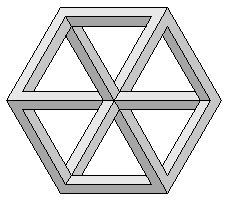
Рисунок 6.
Кокичи Сугихара
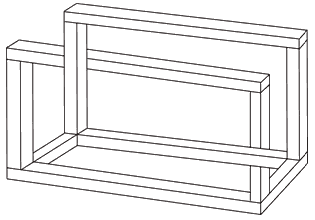

Рисунок 7.
В словосочетании "невозможные" фигуры первое слово взято в кавычки. Почему? Оказывается, "невозможные" объекты в нашем трехмерном мире вполне возможны, только выглядят они совсем не так, как нам диктуют наши стереотипы восприятия чертежей. Реальный объект - прототип иллюзии может иметь разрывы, деформации, но с некоторой точки зрения это легко не заметить - и вот вам чудо во всей красе!

Рисунок 8.
Трюк с разрывом использовали художник Брайан МакКей и архитектор Ахмад Абас, создавая архитектурную достопримечательность города Перта (Австралия). Алюминиевая конструкция с ребристой структурой высотой 13.5 метров (рис. 8) с определенной точки зрения выглядит как "невозможный треугольник" Пенроуза (рис. 9). Эти фотографии специально для журнала "Квант" сделала Анна Звонкова (Австралия).

Рисунок 8.
Впрочем, не обязательно ехать в Австралию. Профессор математики из Токийского университета Кокичи Сугихара, автор оригинальных расчетных методик инженерной графики (http://www.simplex.t.u-tokyo.ac.jp/~sugihara), предлагает воплотить эту идею в бумаге. Для этого он рассчитал "выкройки" трех бумажных брусков, из которых склеивается удивительная конструкция. Сосканируйте или сделайте ксерокопию приведенных на рисунке 10 чертежей, увеличьте их с помощью подходящего редактора изображений (для этих целей, например, хорошо подходит программа Photoshop), распечатайте, а дальше призовите на помощь ножницы и клей. На склеенную модель рекомендуется смотреть одним глазом с расстояния, в 20 раз превышающего характерные размеры модели.
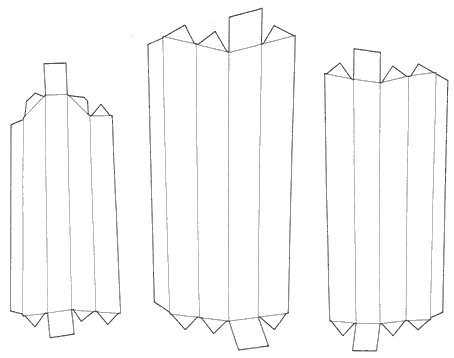
Рисунок 10.
При подготовке этой статьи были использованы материалы сайта http://im-possible.info, а также книги Кокичи Сугихары "Восхищение невозможными объектами".
В. Алексеев, А. Жуков
Данная статья была напечатана в физико-математическом журнале для школьников и студентов "Квант", N6, 2007, в рубрике "Калейдоскоп Кванта".


