Лента Мебиуса
 Лента Мебиуса, сделанная из листа бумаги и клейкой ленты |
Лента Мебиуса (Möbius strip) - трехмерная поверхность, имеющая только одну сторону и одну границу, обладающая математическим свойством неориентируемости. Она была открыта независимо одновременно двумя математиками из Германии Августом Фердинандом Мёбиусом (August Ferdinand Möbius) и Иоганном Бенедиктом Листингом (Johann Benedict Listing) в 1858 году.
Модель ленты Мебиуса может быть легко создана из полоски бумаги, повернув один из концов полоски вполоборота и соединив его с другим концом в замкнутую фигуру. Если начать рисовать карандашом линию на поверхности ленты, то линия уйдет вглубь фигуры и пройдет под начальной точкой линии, как уйдя на "другую сторону" ленты. Если продолжать линию, то она вернется в начальную точку. При этом длина нарисованной линии будет вдвое больше длины полоски бумаги. Этот пример показывает, что у ленты Мебиуса лишь одна сторона и одна граница.
В Евклидовом пространстве, фактически, существует два типа ленты Мебиуса, развернутой вполоборота: одна - развернутая по часовой стрелке, другая - против часовой стрелки.
Геометрия и математика
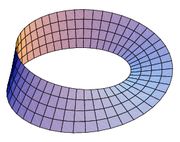 Параметрическое изображение ленты Мебиуса |
Лента Мебиуса может быть представленная параметрической системой уравнений:
где 
и 
.
Этими уравнениями описывается лента
Мебиуса шириной 1, лежащая в плоскости x-y;
внутренний радиус окружности которой
равен 1, центр внутренней окружности
находится в начале координат (0,0,0). Параметр u
движется вдоль ленты, а параметр v - от
одной границы к другой.
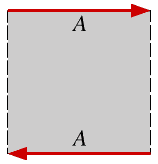 Для получения ленты Мебиуса необходимо совместить два конца полоски так, чтобы направления красных стрелок совпали. |
Иным способом ленту можно представить выражением в полярных координатах:
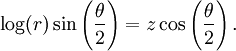
Топологически, лента Мебиуса может быть определена как квадрат [0,1] x [0,1], верх которого соединен с низом в соотношении (x,0) ~ (1-x,1) for 0 ≤ x ≤ 1, как показано на рисунке справа.
Близкие объекты
Тесно связанным с лентой Мебиуса является загадочный объект - бутылка Кляйна. Бутылка Кляйна может быть создана склеиванием двух лент Мебиуса друг с другом вдоль их границ. Эта операция не может быть произведена в трехмерном пространстве без создания пересечений внутри фигуры.
Одна из базовых невозможных фигур невозможный треугольник может быть представлен как лента Мебиуса, если сгладить некоторое его грани. При этом получится лента Мебиуса, описывающая три витка.
Искусство
 Интернациональный символ повторного использования |
 Логотип The Power Architecture |
Лента Мебиуса вдохновила многих художников на создание известных скульптур и картин. Голландский художник М.К. Эшер создан несколько литографий с использованием ленты. Один из известнейших примеров - литография "Лента Мебиуса II", в которой красные муравьи бесконечно ползут по ленте. (см. статью "Математическое искусство М.К. Эшера").
Также лента Мебиуса часто используется в изображениях различных логотипах и торговых марках. Самых яркий пример - международный символ повторного использования.
Приложение. Картины с лентами Мебиуса
Картина ниже Пола Билацика (Paul Bielaczyc) называется "Кельтская лента Мебиуса Как говорит автор, эта картина - объединение различных аспектов его жизни. Кельтские узлы окружают его в его работе, картины М.К. Эшера всегда служат источником вдохновения, а лента Мебиуса имеет отношение к предмету, изучаемому художником.
 Кельтская лента Мебиуса |