Обманутый глаз
4. Невозможные объекты
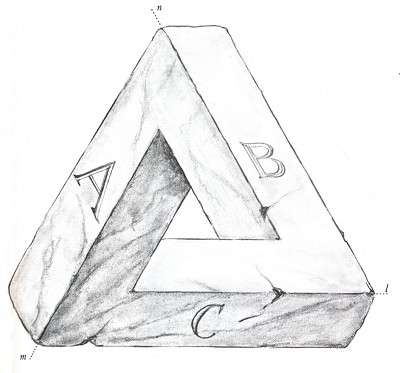
Рисунок 1.
Это невозможный трибар. Данный рисунок не является иллюстрацией пространственного объекта, поскольку такой объект не может существовать. Наш ГЛАЗ принимает данный факт и сам объект без затруднений. Мы можем придумать ряд аргументов в защиту невозможности объектаю Например, грань C лежит в горизонтальной плоскости, в то время как грань A наклонена к нам, а грань B, наклонена от нас, и, если грани A и B расходятся друг от друга, они не могут встретиться в вершине фигуры, как это мы видим в данном случае. Мы можем отметить, что трибар образует замкнутый треугольник, все три балки перпендикулярны друг другу, и сумма его внутренних углов получается равной 270 градусам, что невозможно. Мы можем привлечь на помощь базовые принципы стереометрии, а именно то, что три непараллельные плоскости всегда встречаются в одной точке. Однако, на рисунке 1 мы видим следующее:
- Темно-серая плоскость C встречается с плоскостью B; линия пересечения – l;
- Темно-серая плоскость C встречается со светло-серой плоскостью A; линия пересечения - m;
- Белая плоскость B встречается со светло-серой плоскость A; линия пересечения – n;
- Линии пересечения l, m, n пересекаются в трех разных точках.
Таким образом, рассматриваемая фигура не удовлетворяет одному из основных утверждений стереометрии, что три непараллельные плоскости (в данном случае A, B, C) должны встретиться в одной точке.
Резюмируем: какими бы ни были сложными или простымии ни были наши рассуждения, ГЛАЗ сигнализирует нам о противоречиях без каких-либо объяснений с его стороны.
Невозможный трибар парадоксален в нескольких отношениях. Глазу требуется доля секунды, чтобы передать сообщение: "Это замкнутый объект, состоящий из трех брусков". Мгновение спустя следует: "Этот объект не может существовать...". Третье сообщение может быть прочитано как: "... и, таким образом, первое впечатление было неверным". В теории такой объект должен распадаться на множество линий, не имеющих значимых отношений друг с другом и более не собирающихся в форму трибара. Однако этого не происходит, и ГЛАЗ сигнализирует снова: "Это объект, трибар". Короче говоря, заключение состоит в том, что это и объект и не объект, и в этом состоит первый парадокс. Обе интерпретации имеют одинаковую силу, как если бы ГЛАЗ оставил окончательный вердикт вышестоящей инстанции.
Вторая парадоксальная особенность невозможного трибара возникает из рассуждений о его конструкции. Если брусок A направлен к нам, а брусок B - от нас, и все же они стыкуются, то угол, который они формируют должен лежать в двух местах одновременно, один ближе к наблюдателю, а другой дальше. (То же самое применимо и к двух другим углам, так как объект остается идентичной формы при поворе другим углом вверх.)

Рисунок 2. Бруно Эрнст, фотография невозможного трибара, 1985

Рисунок 3. Gerard Traarbach, "Perfect timing", холст/масло, 100x140 см, 1985, напечатано наоборот

Рисунок 4. Дирк Хуизер, "Куб", irisated screenprint, 48x48 см, 1984
Реальность невозможных объектов
Один из самых трудных вопросов о невозможных фигурах касается их реальности: существуют ли они на самом деле или нет? Естественно, рисунок невозможного трибара существует, и это не подвергается сомнению. Однако, в то же время не вызывает сомнений, что представленная ГЛАЗом для нас трехмерная форма, как таковая, не существует в окружающем мире. По этой причине, мы решили говорить о невозможных объектах, а не о невозможных фигурах (хотя, под таким названием на английском языке они больше известны). Кажется, это удовлетворительное решение данной дилеммы. И все же, когда мы, например, исследуем внимательно невозможный трибар, его пространственная реальность продолжает смущать нас.
Столкнувшись с объектом в разобранном на отдельные части виде, практически невозможно поверить, что, просто соединяя друг другом бруски и кубики, можно получить желаемый невозможный трибар.
Рисунок 3 особенно привлекателен для специалистов по кристаллографии. Объект представляется медленно растущим кристаллом, кубы вставляются в имеющуюся кристаллическую решетку без нарушения общей структуры.
Фотография на рисунке 2 – реальна, хотя трибар, составленный из коробок для сигар и сфотографированный под определенным углом, – нереален. Это визуальная шутка, придуманная Роджером Пенроузом – соавтором первой статьи и невозможном трибаре.
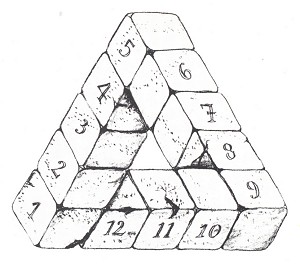
Рисунок 5.
На рисунке 5 изображен трибар, составленный из пронумерованных блоков размером 1х1х1 дм. Простым подсчетом блоков мы можем выяснить что объем фигуры 12 дм3, и прощадь – 48 дм2.
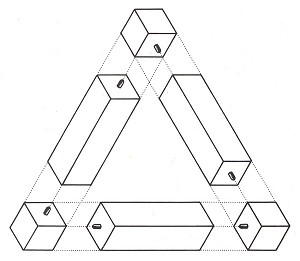
Рисунок 6.
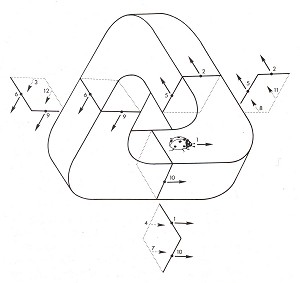
Рисунок 7.
Аналогичным способом мы можем подсчитать расстояние, которая пройдет божья коровка по трибару (рисунок 7). Центральная точка каждого бруска пронумерована, и направление движения отмечено стрелками. Таким образом, поверхность трибара представляется как длинная непрерывная дорога. Божья коровка должна совершить четыре полных круга, прежде чем вернется в исходную точку.
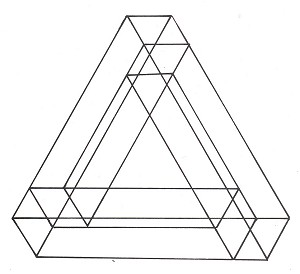
Рисунок 8.
Вы можете начать подозревать, что невозможный трибар имеет какие-то секреты на своей невидимой стороне. Но без труда можно нарисовать прозрачный невозможный трибар (рис. 8). В данном случае все четыре стороны видимы. Тем не менее, объект продолжает выглядеть вполне реальным.
Давайте зададим вопрос еще раз: что в действительности делает трибар фигурой, которая может интерпретироваться таким множеством способов. Надо помнить, что ГЛАЗ обрабатывает изображение невозможного объекта с сетчатки также, как и изображения обычных предметов - стула или дома. Результатом является "пространственное изображение". На этом этапе нет разницы между невозможным трибаром и обычным стулом. Таким образом, невозможный трибар существует в глубинах нашего мозга на том же самом уровне, что и всех остальные объекты, окружающие нас. Отказ глаза подтвердить трехмерную "жизнеспособность" трибара в реальности никоим образом не уменьшает факта присутствия невозможного трибара у нас в голове.
В главе 1 мы встретились с невозможным объектом, чье тело исчезало в никуда. В карандашном рисунке "Пассажирский поезд" (рис. 11) Fons de Vogelaere тонко воспользовался тем же принципом с усиленной колонной в левой части картины. Если мы проследим взглядом по колонне сверху вниз, или закроем нижнюю часть картины, то увидим колонну, которая поддерживается четырьмя опорами (из которых видны только две). Однако, если посмотреть снизу на ту же колонну, то увидим достаточно широкий проем, сквозь который может проехать поезд. Твердые каменные блоки в то же самое время оказываются ... тоньше воздуха!
Данный объект достаточно прост для категоризации, но оказывается достаточно сложным, когда мы начинаем его анализировать. Исследователи, такие как Broydrick Thro, показали, что само описание данного явления приводит к противоречиям. Конфликт в одной из границ. ГЛАЗ сначала просчитывает контуры, а затем собирает из них фигуры. Путаница возникает, когда контуры имеют сразу два назначения в двух разных фигурах или частях фигуры, как на рисунке 11.
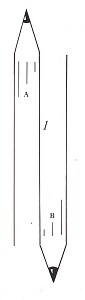
Рисунок 9.
Аналогичная ситуация возникает и на рисунке 9. В данной фигуре линия контура l проявляется и как граница формы A и как граница формы B. Однако, она не является границей обеих форм одновременно. Если ваши глаза посмотрят сначала на верхнюю часть рисунка, то, опускаясь взглядом вниз, линия l будет восприниматься, как граница формы A и будет оставаться такой до тех пор, пока не обнаружится, что A – открытая фигура. В этой точке ГЛАЗ предлагает вторую интерпретацию для линии l, а именно, что она является границей формы B. Если последуем взглядом обратно вверх по линии l, то мы снова вернемся к первой интерпретации.
Если бы это было единственной двусмысленностью, то мы могли бы говорить о пиктографической двойственной фигуре. Но заключение осложняется дополнительными факторами, такими как явление исчезновения фигуры на фоне заднего плана, и, в особенности, пространственным представлением фигуры ГЛАЗом. В связи с этим в можете уже по-другому взглянуть рисунки 7,8 и 9 из главы 1. Хотя эти типы фигур проявляют себя как настоящие пространственные объекты, мы можем временно назвать их невозможными объектами и описать их (но не объяснить) в следующих общих понятиях: ГЛАЗ вычисляет на основе этих объектов две различные взаимоисключающие трехмерные формы, которые, тем не менее, существуют одновременно. Это можно видеть на рисунке 11 в том, что, как нам кажется, представляет собой монолитную колонну. Однако, при повторном осмотре, она представляется открытой, с просторным промежутком посередине, через который, как показано на рисунке, может проехать поезд.

Рисунок 10. Arthur Stibbe, "In front and behind", картон/акрил, 50x50 см, 1986

Рисунок 11. Fons de Vogelaere, "Пассажирский поезд", рисунок карандашом, 80x98 см, 1984
Невозможный объект как парадокс
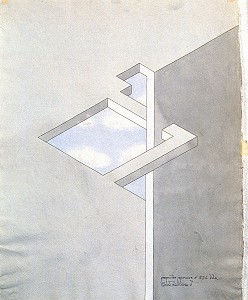
Рисунок 12. Oscar Reutersvärd, "Perspective japonaise n° 274 dda", раскрашенный рисунок тушью, 74x54 см
В начале данной главы мы увидели невозможный объект, как трехмерный парадокс, то есть изображение, чьи стереографические элементы входят в противоречие друг с другом. Перед тем, как исследовать данный парадокс глубже, необходимо понять, существует ли такое явление как пикторафический парадокс. На самом деле он существует – подумайте о русалках, сфинксах и других сказочных существах, часто встречающихся в изобразительном искусстве Средних веков и раннего Возрождения. Но в данном случае не работа ГЛАЗа нарушается таким пиктографическим уравнением, как женщина+рыба=русалка, а наши знания (в частности, знания биологии), согласно которым такая комбинация недопустима. Только там, где пространственные данные на изображении с сетчатки взаимно противоречат друг другу, возникает сбой "автоматической" обработки данных ГЛАЗом. ГЛАЗ не готов обрабатывать настолько странный материал, и мы свидетельствуем новый для нас зрительный опыт.

Рисунок 13a. Harry Turner, рисунок из серии "Paradoxical patterns", смешанная техника, 1973-78
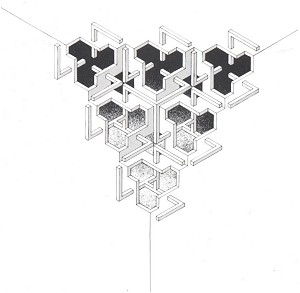
Рисунок 13b. Harry Turner, "Corner", смешанная техника, 1978
Мы можем разделить пространственную информацию, содержащуюся в изображении с сетчатки глаза (когда смотрим только одним глазом) на два класса – природный и культурный. Первый класс содержит информацию, на которую культурная среда человека не оказывает никакого влияния, и которая также обнаруживается на картинах. К такой истинной "неиспорченной природе" относится следующее:
- Объекты одинакового размера выглядят тем меньше, чем дальше они находятся. Это основной принцип линейной перспективы, которая играет главную роль в изобразительном искусстве со времен Возрождения;
- Объект, который частично загораживает другой объект, находится ближе к нам;
- Объекты или части объекта, соединенные друг с другом, находятся на одинаковом расстоянии от нас;
- Объекты, находящиеся сравнительно далеко от нас, будут менее различимы и будут скрыты голубой дымкой пространственной перспективы;
- Та сторона объекта, на которую падает свет, ярче, чем противоположная сторона, и тени указывают в направлении противоположном источнику света.

Рисунок 14. Zenon Kulpa, "Невозможные фигуры", тушь/бумага, 30x21 см, 1980
В культурном окружении два следующих фактора играют важную роль в нашей оценке пространства. Люди создали свое жилое пространство таким, что в нем преобладают прямые углы. Наша архитектура, мебель и многие инструменты, по существу, составлены из прямоугольников. Можно сказать, что мы упаковали наш мир к прямоугольную систему координат, в мир прямых линий и углов.

Рисунок 15. Mitsumasa Anno, "Сечение куба"
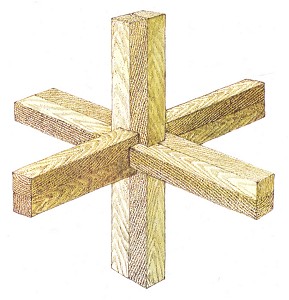
Рисунок 16. Mitsumasa Anno, "Сложная деревянная головоломка"

Figure 17. Monika Buch, "Синий куб", акрил/дерево, 80x80 см, 1976
Таким образом, наш второй класс пространственной информации - культурный, ясен и понятен:
- Поверхность – это плоскость, которая продолжается до тех пор, пока другие детали не сообщат нам, что она не закончилась;
- Углы, в которых встречаются три плоскости, определяют три основных направления, в связи с чем, зигзагообразные линии могут указывать на расширение или сужение.

Рисунок 18. Tamas Farcas, "Кристалл", irisated print, 40x29 см, 1980
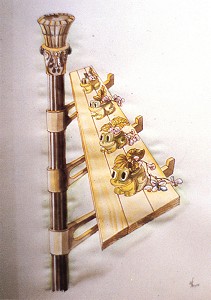
Рисунок 19. Frans Erens, акварель, 1985
В нашем контексте, различие между природным и культурным окружением очень полезно. Наше зрительное чувство развивалось в природном окружении, и также оно имеет поразительную способность точно и безошибочно обрабатывать пространственную информацию из культурной категории.
Невозможные объекты (по крайней мере, бóльшая их часть) существуют благодаря наличию взаимно противоречащих друг другу пространственных утверждений. Например, на картине Жоса де Мея "Double-guarded gateway to the wintery Arcadia" (рис. 20), плоская поверхность, образующая верхнюю часть стены распадается внизу на несколько плоскостей, находящихся на разном расстоянии от наблюдателя. Впечатление о разных расстояниях также формируется перекрывающимися частями фигуры на картине Arthur Stibbe "In front and behind" (рис. 10), которые противоречат правилу плоской поверхности. На акварельном рисунке Frans Erens (рис. 19), полка, изображенная в перспективе, уменьшающимся в размере концом сообщает нам, что она расположена горизонтально, уходя вдаль от нас, и она также прикреплена к опорам таким образом, чтобы находиться вертикально. На картине "The five bearers" Fons de Vogelaere (рис. 21) мы будем ошеломлены количеством стереографических парадоксов. Хотя в картине не содержится парадоксальных перекрытий объектов, в ней много парадоксальных соединений. Представляет интерес способ, которым центральная фигура соединена с потолком. Пять фигур, подпирающих потолок, соединяют парапет и потолок настолько большим количеством парадоксальных соединений, что ГЛАЗ отправляется в бесконечный поиск точки, с которой лучше рассматривать их.

Рисунок 20. Jos de Mey, "Double-guarded gateway to the wintery Arcadia", холст/акрил, 60x70 cm, 1983
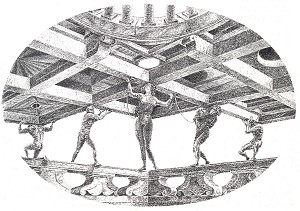
Рисунок 21. Fons de Vogelaere, "The five bearers", рисунок карандашом, 80x98 см, 1985
Вы можете подумать, что при помощи каждого возможного типа стереографического элемента, который появляется на картине, относительно просто составить систематический обзор невозможных фигур:
- Те, что содержат элементы перспективы, находящие во взаимном конфликте;
- Те, в который элементы перспективы в конфликте с пространственной информацией, указанной перекрывающимися элементами;
- и т.д.
Однако, мы вскоре обнаружим, что не сможем обнаружить существующие примеры для многих таких конфликтов, в то время как некоторые невозможные объекты будет трудно вписать в подобную систему. Тем не менее, такая классификация позволит нам обнаружить еще много до сих пор неизвестных типов невозможных объектов.

Рисунок 22. Shigeo Fukuda, "Images of illusion", screenprint, 102x73 см, 1984
Определения
В заключение данной главы давайте попытаемся дать определение невозможным объектам.
В моей первой публикации о картинах с невозможными объектами М.К. Эшера, которая появилась примерно в 1960 году, я пришел к следующей формулировке: возможный объект всегда может рассматриваться как проекция - представление трехмерного объекта. Однако, в случае невозможных объектов, не существует трехмерного объекта, чьим представлением является данная проекция, и в данном случае мы можем называть невозможный объект – иллюзорным представлением. Данное определение является не только неполным, но и неправильным (к этому мы еще вернемся в главе 7), так как оно относится только математической стороне невозможных объектов.
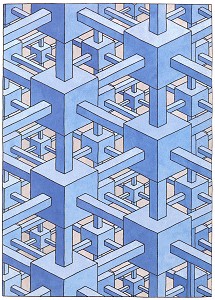
Рисунок 23. Oscar Reutersvärd, "Cubic organization of space", раскрашенный рисунок тушью, 29x20.6 cm.
В действительности данное пространство не является заполненным, так как кубы большего размера не связаны с кубами меньшего размера.
Зенон Кульпа предлагает следующее определение: изображение невозможного объекта – это двухмерная фигура, создающее впечатление существующего трехмерного объекта, причем эта фигура не может существовать так, как мы ее пространственно интерпретируем; таким образом, любая попытка создать его ведет к (пространственным) противоречиям, которые отчетливо видны зрителю.
Последнее замечание Кульпы предлагает один практический путь выяснения, является ли объект невозможным или нет: просто попробуйте создать его самостоятельно. Вы вскоре увидите, возможно даже до начала конструирования, что вы не сможете этого сделать.
Я предпочел бы определение, которое подчеркивает, что ГЛАЗ при анализе невозможного объекта приходит к двум противоречивым заключениям. Мне больше нравится именно такое определение, так как оно охватывает причину этих взаимно конфликтующих заключений, и, кроме этого, разъясняет тот факт, что невозможность – это не математическое свойство фигуры, а свойство интерпретации фигуры зрителем.
На основании этого я предлагаю следующее определение:
Невозможный объект обладает двухмерным представлением, которое ГЛАЗ интерпретирует как трехмерных объект, причем в то же время ГЛАЗ определяет, что данный объект не может быть трехмерным, так как пространственная информация, содержащаяся в фигуре, - противоречива.

Рисунок 24. Oscar Reutersväird, "Impossible four-bar with Crossbars"

Рисунок 25. Bruno Ernst, "Mixed illusions", фотография, 1985
