Adventures with Impossible Figures

'Ascending and Descending' by Escher (1960)

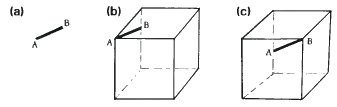
When we look at a drawing of a line segment entirely on its own, we cannot know what it represents. In (a) the line segment AB looks straight and it might be a line. However, it could even be a circle seen sideways in the plane of the observer. We cannot tell. Even if we know that it is a straight line, we still cannot say what its orientation in space is. If the context is as in (b), then A is higher and nearer than B. In (c), A is further away and lower than B. Yet in all three cases the actual marks AB on the paper are identical in size and direction.

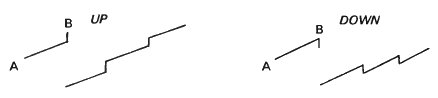
The addition of an extra line segment to AB does give more information, especially if it is repeated several times. However, more of the context is necessary before we can be sure what is meant.

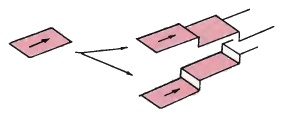
There is no doubt in these sketches that one set of stairs leads upwards and the other leads downwards. The repeated and joined line segments are supported with other visual information to make a convincing impression.

'Ascending and Descending'

That both kinds of staircase could be combined to make a new impossible figure was first put forward by L.S. & R. Penrose in 1958. In the article which also introduced the impossible tri-bar, they explained how a staircase could rise or fall endlessly and yet return to the same level. Escher borrowed the idea and produced the splendid lithograph 'Ascending and Descending' (1960) which is shown above. The hooded figures toil endlessly upwards and downwards, clockwise and anticlockwise, lost in thought about the impossibility of their situation.

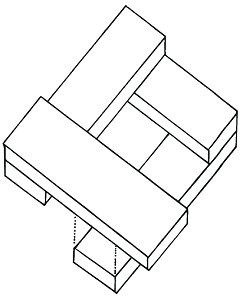
Since a drawing of the tread of a staircase has no sense of direction, we must introduce other visual signposts to indicate whether the stairway leads upwards or downwards. This drawing shows a stairway which descends in a clockwise direction using only four steps. As a result there is a gap of two stair heights when the circuit is completed. All the visual indicators are consistent and there is no impossibility.

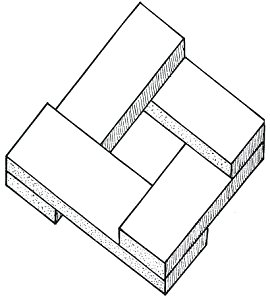
The previous drawing has now been modified to introduce false indicators and as a result we have created an impossible staircase with only four treads. Descend in a clockwise direction. Ascend in an anticlockwise direction. Follow the mysterious stairway which leads to nowhere at all!

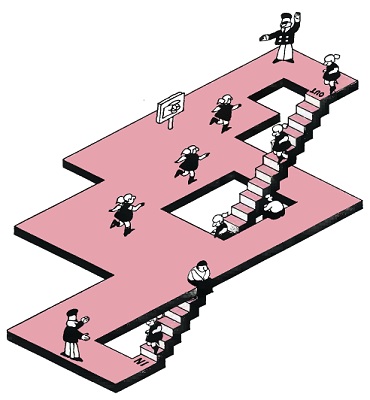
This is an adaptation of one of Oscar Reutersvärd's many drawings of impossible staircases. The top stairs of a long staircase is reconnected to the bottom stair by a flat plane. I have added figures and signs to accentuate the contradiction of 'up' and 'down', 'in' and 'out'. The behaviour of the figures draws attention to the fact that there is no possible escape, although some appear not to have realised it yet. The men gave up a long time ago!

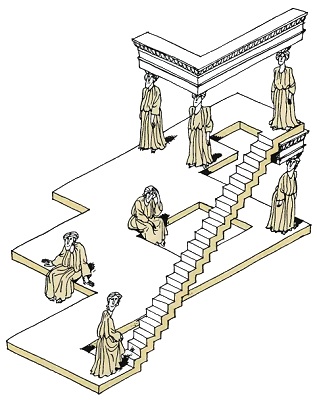
The Greeks were renowned for their power of abstract thought. But is the problem posed by this drawing too much even for them? Would it give a Caryatid a headache.

Level and yet Rising

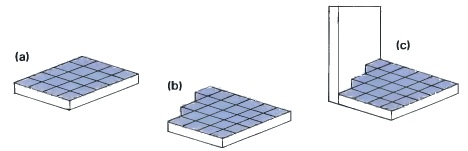
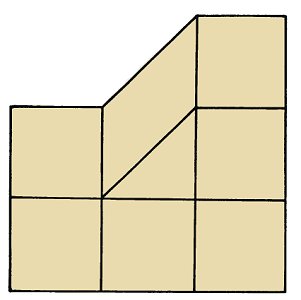
These three drawings show just how influenced we are by the clues and visual signposts which tell us of position in space. In (a) we have no difficulty in interpreting it as a flat plane divided into square tiles. In (b) the far edge could be jagged, although the eye is rather tempted to perceive them as steps. In (c) we have added further indications of a vertical wall and the eye jumps to the conclusion that there is indeed a rising staircase. Of course that then raises the problem of explaining how it is that the right hand edge is still flat!

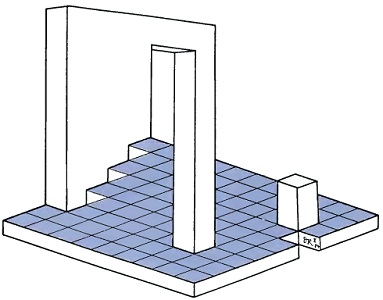
Add a few more details and we have a delightfully impossible figure.

Here are further experiments with tiled floors which have produced two more impossible figures.

Let us now look back at Escher's 'Waterfall' on page 17. Notice how he has indicated which way the water must flow by making the sides of the channel step downwards as an impossible stairway.

The success with square tiles in the previous section suggested that it would be interesting to experiment with a chess-board and see if any new intriguing figures could be devised. This proved to be the case and it was not difficult to make some convincing impossible figures, this time in photographic form. The effect seems to demand remarkably few squares and only two squares have had to be modified. I hope that you agree that the effect is quite strong.

Below is a real photograph of a perfectly flat board. The queen is both higher than her subjects and on exactly the same level!

The queen stands on the same level as the rook and higher than the pawn. But the rook and the pawn stand at the same level.

Photographing the chess-board and its reflection in a mirror does not destroy the illusion at all.