Adventures with Impossible Figures

In the real world a flat surface cannot be both horizontal and vertical at the same time. Everyone knows that and so perhaps this would be a good new area to explore in our search for new impossible figures.

We have no problem in seeing drawing (a) as a sketch of a horizontal surface. In (b) the surface PQRS seems to be vertical. Can we combine the two?

Let us now look carefully at the trapezium PQRS. Notice how we have taken the direction of PQ from (a) and the direction of RS from (b). If we concentrate on the left hand edge of the drawing it is possible to interpret it as a horizontal plane. The right hand edge could be a vertical plane. Can we force both interpretations at the same time by adding more and contradictory visual signposts?

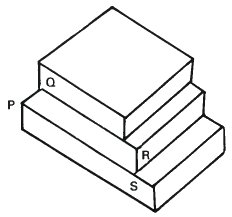
The solidity of the blocks forces us to see PQ as horizontal and RS as vertical in spite of the fact that PQRS is a trapezium. The same plane is both horizontal and vertical at the same time and we can add another new impossible figure to our collection!

A Temple to Impossibility?

Many people have devised impossible drawings where a plane or planes can be seen as horizontal and vertical at the same time. I discovered this interesting variation only recently. It is an impossible step-pyramid where the number of steps seems to grow in an almost miraculous way. On the left side there are three steps, in the centre five and on the right there are nine. Yet each interpretation seems totally convincing within its own region of the figure. All steps lead upwards to the temple on top. Is this not the perfect design for a temple to impossibility?

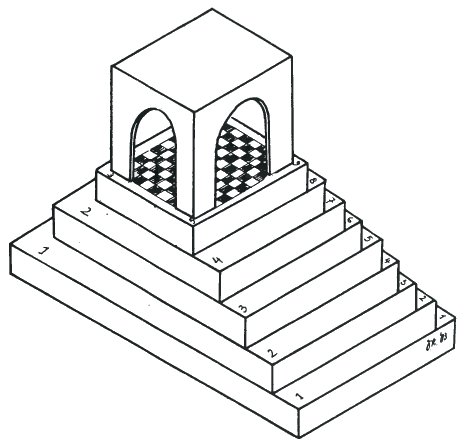
All steps are equal, but some are more equal than others!

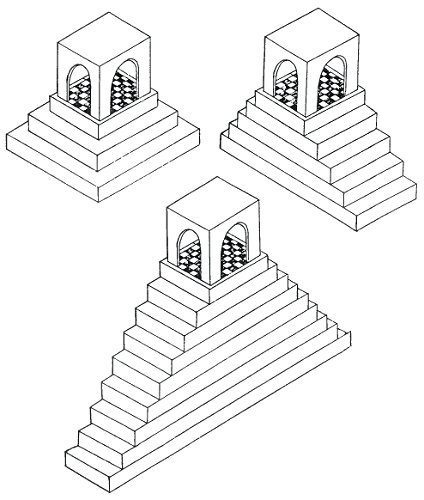
The three sketches on this page show the three elements from which the figure opposite was built. None is impossible and you can climb up to each real temple by using three, five or nine real stairs.

This figure shows an impossible temple drawn with perspective. Most of the illustrations in this book have been drawn using an isometric projection and true perspective has largely been ignored. This has meant that parallel lines have been drawn parallel and not converging to a vanishing point. We have also ignored the fact that in a perspective drawing objects which are further away must be drawn smaller. Curiously, the eye does not seem very sensitive to these indicators of position in space, at least for the kind of figures we have met in this book.

It is worth looking back at pages 20 and 74 to see figures in which different kinds of isometric projection have been used for the walls and for the ceilings. In both drawings it was important to include both the ceiling and the floor in order to strengthen the feeling of false perspective which so adds to the strangeness of the rooms.