Cameron Browne. Impossible fractals

The tri-bar (Figure 1, left) is described by Ernst [3] as the simplest yet most fascinating of all impossible objects, and is one of the most widely recognized. The illusion is created by the ambiguous use of parallel lines drawn in different perspectives, so that the figure appears to perpetually turn out of the page when traversed in a clockwise direction. The two corners at the end of each bar are interpreted as lying perpendicular to each other, which Ernst points out would give a total internal angle of 360° and hence defy a fundamental property of triangles; this figure cannot be physically constructed as a closed shape with perpendicular corners and straight arms.

Figure 1. The tri-bar, the Koch snowflake and the Sierpinski gasket.

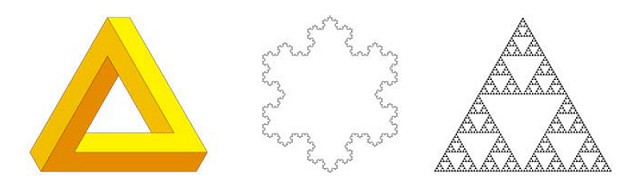
The tri-bar was invented in 1934 by Oscar Reutersvärd, a Swedish graphic artist who went on to become the world's greatest exponent of impossible figures, producing several thousand until his death in 2002. The tri-bar is often called the Penrose Triangle after mathematician Roger Penrose, who independently rediscovered it and popularised it in the 1958 article "Impossible Objects: A Special Type of Visual Illusion" co-written with his father [2]. It is also known as the Escher Triangle as Dutch graphic artist M. C. Escher embraced the principles it represented and included its design in many of his works, most famously the perpetual stream of his 1961 lithograph "Waterfall" [5].

We call this figure the tri-bar in keeping with Ernst's terminology [3], which may be extended to multibar figures with more than three sides. Multibars are generally drawn on an isometric grid with the following design rules in mind:

1. Local geometry and shading should be consistent;
2. Adjacent regions should not share the same colour; and
3. The least number of colours should be used (three colours will generally suffice, although four are required in some cases).