Cameron Browne. Impossible fractals
4. Forks
The Devil's fork, also known as the impossible fork, Devil's pitchfork, Devil's tuning fork or the blivet [1], is another famous impossible object (Figure 5, left). Similar figures had been devised by Reutersvärd since 1958 [3] but it was not until Schuster's description in a 1964 article [7] and its appearance on the cover of the March 1965 issue of Mad magazine that the Devil's fork became widely known. This illusion involves confusion between the figure and its background. Its local geometry is valid at its open and closed ends on the left and right, but a perceptual shift occurs as the eye travels between the two.
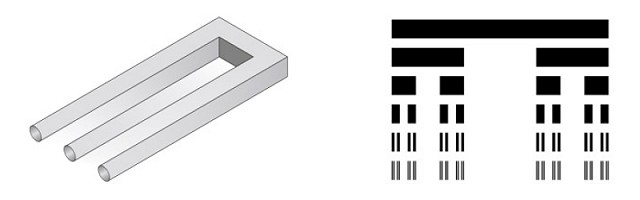
The Cantor set (Figure 5, right) is the simplest of fractals, involving the recursive removal of the middle third of a given line segment and its subsegments. Figure 6 shows how Cantor-style subdivision may be applied to the Devil's fork to increase the number of prongs, allowing some creativity in their configuration.

Figure 6 (top left) shows the Devil's fork turned into a Devil's gatling gun after two levels of subdivision and replacement of the fork's alternating spaces with an additional layer of prongs to suggest a round configuration. Figure 6 (bottom left) shows a similar design except that the prongs are realised as square bars of uneven length, after a design by Reutersvärd [3]. The Devil's comb (right) shows the basic fork after three levels of Cantor-style subdivision.
