Hypercube
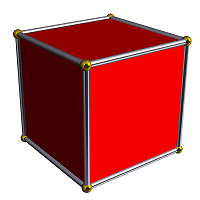 A projection of cube into two-dimensional image |
In geometry, a hypercube is an n-dimensional analogue of a square (n = 2) and a cube (n = 3). It is a closed convex figure consisting of groups of opposite parallel line segments aligned in each of the space's dimensions, at right angles to each other.
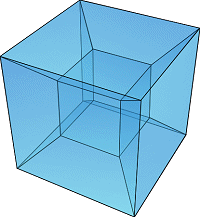
It's also known as tesseract. The tesseract is to the cube as the cube is to the square; or, more formally, the tesseract can be described as a regular convex 4-polytope whose boundary consists of eight cubical cells.
According to the Oxford English Dictionary, the word "tesseract" was coined and first used in 1888 by Charles Howard Hinton in his book "A New Era of Thought", from the Ionic Greek "τεσσερες ακτινες" ("four rays"), referring to the four lines from each vertex to other vertices. Alternately, some people have called the same figure a "tetracube".
An n-dimensional hypercube is also called an n-cube. The term "measure polytope" is also used, but seems to refer only to the hypercube with unit sides (see Coxeter 1973) and is rare.
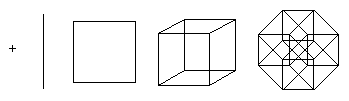
 A projection of hypercube into two-dimensional image |
A point is a hypercube of dimension zero. If one moves this point one unit length, it will sweep out a line segment, which is the measure polytope of dimension one. If one moves this line segment its length in a perpendicular direction from itself; it sweeps out a two-dimensional square. If one moves the square one unit length in the direction perpendicular to the plane it lies on, it will generate a three-dimensional cube. This can be generalized to any number of dimensions. For example, if one moves the cube one unit length into the fourth dimension, it generates a 4-dimensional measure polytope or tesseract.
The family of hypercubes is one of the few regular polytopes that are represented in any number of dimensions. The dual polytope of a hypercube is called a cross-polytope.
Elements
A hypercube of dimension n has 2n "sides" (a 1-dimensional line has 2 end points; a 2-dimensional square has 4 sides or edges; a 3-dimensional cube has 6 faces; a 4-dimensional tesseract has 8 cells). The number of vertices (points) of a hypercube is 2n (a cube has 23 vertices, for instance).
The number of m-dimensional hypercubes on the boundary of an n-cube is
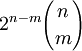
For example, the boundary of a 4-cube contains 8 cubes, 24 squares, 32 lines and 16 vertices.
| n-cube | Names | Vertices (0-faces) |
Edges (1-faces) |
Faces (2-faces) |
Cells (3-faces) |
(4-faces) | (5-faces) | (6-faces) | (7-faces) | (8-faces) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-cube | Point | 1 | ||||||||
| 1-cube | Digon | 2 | 1 | |||||||
| 2-cube | Square | 4 | 4 | 1 | ||||||
| 3-cube | Cube Hexahedron |
8 | 12 | 6 | 1 | |||||
| 4-cube | Tesseract octachoron |
16 | 32 | 24 | 8 | 1 | ||||
| 5-cube | Penteract deca-5-tope |
32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-cube | Hexeract dodeca-6-tope |
64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-cube | Hepteract tetradeca-7-tope |
128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-cube | Octeract hexadeca-8-tope |
256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-cube | Eneneract octadeca-9-tope |
512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Projections to 2 dimensions
The construction of a hypercube can be imagined the following way:
- 1-dimensional: Two points A and B can be connected to a line, giving a new line AB.
- 2-dimensional: Two parallel lines AB and CD can be connected to become a square, with the corners marked as ABCD.
- 3-dimensional: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH.
- 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.
This structure is not easily imagined but it is possible to project tesseracts into three- or two-dimensional spaces. Furthermore, projections on the 2D-plane become more instructive by rearranging the positions of the projected vertices. In this fashion, one can obtain pictures that no longer reflect the spatial relationships within the tesseract, but which illustrate the connection structure of the vertices, such as in the following examples:
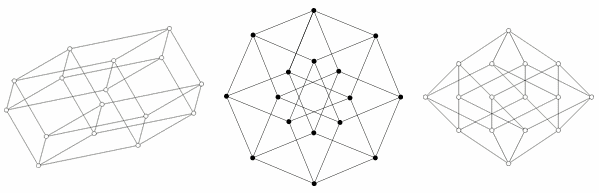
The first illustration shows how a tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. The second picture accounts for the fact that each edge of a tesseract is of the same length. This picture also enables the human brain to find a multitude of cubes that are nicely interconnected. The third diagram finally orders the vertices of the tesseract with respect to the distance along the edges, with respect to the bottom point. This view is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
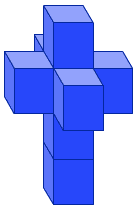 Unfolded tesseract |
Unfolding the tesseract
The tesseract can be unfolded into eight cubes, just as the cube can be unfolded into six squares. An unfolding of a polyhedron is called a net. There are 261 distinct nets of the tesseract (see the adjacent figure for an example of one of the 261 nets).
 Crucifixion (Corpus Hypercubus) by Salvador Dalí (1954) |
Hypercube in art
Hypercube have appeared in science fiction literature since 1940 when Robert A. Heinlein in "And He Built a Crooked House" where he described a house built as unfolded tesseract. It collapsed, becoming a real 4-dimensional tesseract. Then tesseract appears in many books and novels.
The movie "Cube 2: Hypercube" focuses on eight strangers trapped inside a net of hypercubes.
The painting "Crucifixion (Corpus Hypercubus)", by Salvador Dalí, 1954, depicts the crucified Jesus upon the net of a hypercube. It is featured at the Metropolitan Museum of Art in New York.
Conclusion
As hypercube is one of the simplest four dimensional figures it clearly shows the complexity and singularity of the fourth dimension. That which seems impossible in our three-dimensional space is possible in fourth dimension, for example, impossible figures. The bars of four-dimensional impossible triangle can be connected at right angles and it will not be distorted from any point of view as distinct from three-dimensional impossible triangle (see "Impossible figures in the real world").
The article is based on matherials of Wikipedia
