[ Return to contents ]

1. Introduction: impossible objects and ambiguous figures

Figure 1. Léander, "Statue of an impossible tribar", oil on canvas, 70x70 cm, 1984

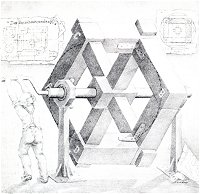
The author of the drawing opposite (fig. 2) has combined considerable mathematical imagination with a generous portion of technical skill to produce a new type of flywheel. Its individual components are detailed in the plans pinned to the wall on the left, while the frontal view of the axle hanging on the right reveals the design of a quadratic wheel. But the viewer remains rightly unconvinced: no such wheel can be built. There is nothing impossible about the six beams composing the outer rim of the wheel, even though they do not lie within the same plane, but the four spokes simply cannot be attached as shown. The inventor of this particular wheel challenges us to find even one join within the entire composition which is demonstrably false. But as we soon discover, all are correct. And yet... the object illustrated here in such precise detail cannot exist in space: it is an impossible object! Only by separating the joins at certain points do we arrive at an object which can indeed be built - Figure 3 shows one of the possibilities. The result, however, is something entirely different to what the inventor originally intended: a bizarre three-dimensional construction whose possibility has left it useless...

Figure 2. Sandro del Prete, "The quadrature of the wheel", pencil drawing	Figure 3

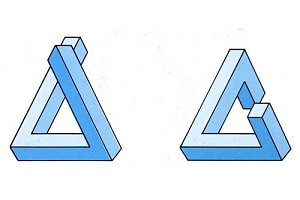
Sandro del Prete has incorporated two impossible tri-bars into this "impossible wheel". The tribar is the simplest and at the same time the most fascinating of all the impossible objects we know (fig. 4). It looks very "real", and yet it cannot exist. It is a most peculiar nothing.

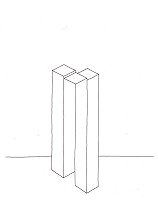
Yet its impossibility is not as absolute as that of a square circle, for example, which can neither be imagined nor drawn. The impossible objects with which we are concerned can, strangely enough, be easily visualized, wherein lies their attraction. They open up a new world and thereby illuminate something of the incredibly complex process that we call vision. Is an impossible tribar really impossible? Figure 5 shows how, by separating the arms of such a tribar at certain points, we arrive at an object that can be built; it is immediately obvious that we have thereby transformed it into something entirely different.

Figure 4. Oscar Reutersvärd, impossible tri-bar	Figure 5.

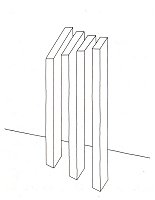
Sandro del Prete's Three Candles (fig. 6) represent a very different category of impossible object to that of the impossible tri-bar. Are there three candles, or just two? If we lower our eyes from the middle flame, we find the candle on which it is burning fades mysteriously into nothing. At the same time, if we raise our eyes from what appears to be the square base of the right-hand candle, we find that its left-hand side vanishes into the background, so that only the right side remains. A characteristic feature of such impossible objects is that they can only be rendered in black and white; they cannot be coloured in. Three further drawings by Oscar Reutersvärd are also reproduced on this page (figs. 7-9). There is something positively irritating about such images, in which the figure which initially appears so solid slips away beneath our very eyes. Matter seems to vanish into void.

Figure 6. Sandro del Prete, "Three Candels", pencil drawing

Figure 7.	Figure 8.	Figure 9.

Ambiguous figures form a different category again. In contrast to impossible objects, which do not exist and which represent nothing, ambiguous figures may suggest more than one three-dimensional reality at once. Thus we can interpret the figure at the centre of Monika Buch's painting (fig. 10) as both a cube projecting outwards and a concave cubic space. It would be perfectly possible to design and build two different three-dimensional models of the picture, one illustrating each interpretation. As we shall see in Chapter 3, every image projected onto the retina of the eye is essentially ambiguous, whether we are looking at a picture or at real objects around us. Fortunately, this rarely causes us problems in everyday life, since our consciousness accepts only those of the many pieces of information provided by the image on the retina which correspond with reality. We only speak of ambiguous figures where two (and sometimes even more) interpretations of one and the same figure are plausible.

Figure 10. Monika Buch, "Illusory cube", acrylic on fibreboard, 60x60 cm, 1983. Three large bars, themselves each composed of twenty-five small bars, form a "concave cube". After a few seconds, this suddenly inverts into a convex cube. Before the EYE switches back to the first, concave interpretation, we are able to see how the thinner bars are transformed into transparent streaks, like shafts of coloured light, illuminating the cube from three sides.

The first scientists to make a study of impossible objects and ambiguous figures listed both categories under the heading of "optical illusions". This is somewhat misleading, however, since in this way the unique character of such objects is overlooked. Optical illusions are things which we see but which either do not exist in reality or whose real nature is different. We regularly encounter optical illusions in our daily lives without recognizing them as such, simply because we are constantly making allowances for them. For example, although the moon may appear to follow us as we walk down the street at night, we know full well that it is actually standing still. Similarly, the moon appears much bigger when low on the horizon than it does when high in the sky, but we do not therefore think the moon expands and contracts every night. When I look out of my window down onto the houses below, they appear no larger than the jar on my windowsill, yet I give the phenomenon no second thought. Optical illusions are for the most part an integral aspect of our perceptual expectations.

Figure 11. A.J.W.M. Thomassen, "Anachronistic psychological laboratory", 1975

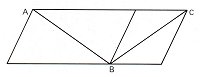
Certain forms of optical illusion nevertheless possess an unusual character; some are even named after their "inventor" or discoverer. In a painting by Prof. A.J.W.M. Thomassen (fig. 11), we see, amongst other things, the Sander parallelogram (1926; fig. 12). If this particular optical illusion is new to you, take a ruler and measure for yourself the difference between the long AB line and the short BC line! The Fraser illusion (1908; fig. 13) demonstrates the large extent to which the direction of lines is determined by additional factors: although the letters of the word LIFE appear to lie crooked, they in fact stand vertical and parallel. Judging the size of a circle is equally dependent upon the objects surrounding it (Lipps, 1897; fig. 14): the centre circles in the two patterns are both the same size.

Figure 12. The Sander illusion

Figure 13. The Fraser illusion

Figure 14.

Such optical illusions have been the subject of research for over one hundred and fifty years, and they have much to teach us about the functioning of our sense of sight. The ambiguity of figures was discussed by Necker as early as 1832, although impossible objects only began to attract attention from 1958 on, through the work of Penrose and his son, whose impossible tri-bar also features in Thomassen's painting.

In this book we shall be showing, amongst other things, that ambiguous figures and impossible objects are important not simply for the peculiar light which they throw upon the phenomenon of vision, but because their discovery by artists has opened up previously unexplored fields in the history of art.

[ Return to contents ]