The Eye Beguiled
7. Models
Of course it is impossible to build a real-life, three-dimensional model of an impossible object; if you could, it wouldn't be one! When we talk of a model of an impossible object, we mean a three-dimensional object which can be made to look like an impossible object if viewed or photographed from a certain angle. Such a model, incidentally, bears no similarity to the impossible object which is perceived by the EYE. Figure 1 shows a photograph of an impossible four-bar in which the true nature of the model is revealed by a mirror. It is patently clear that no similarity exists between the object and the image in the mirror.

Figure 1. Bruno Ernst, photograph of an impossible four-bar and its reflection in the mirror.
As the first impossible objects became known, people lost no time in trying to make models of them. One of the first such models, very popular in its day, was the Crazy crate, a model of Escher's impossible cube produced by American opthalmologist Cochran out of two separate pieces.
For almost every impossible object we can invent a number of different models. Figure 2 demonstrates how we continue to see one and the same triangle, ABC, however differently oriented its lines in space. The lines themselves can assume all sorts of different forms and be broken or curved - projected onto our retina, they always supply the same image.
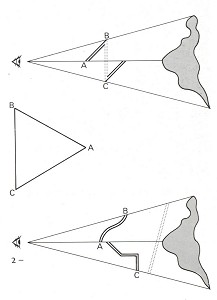
Figure 2.
If we take bars instead of lines and trim their ends appropriately,
the EYE perceives their spatial arrangement as an impossible tri-bar.
The Ames transformation
The way in which three-dimensional constructions acquire, through their projection onto the retina, a spatial coherence which does not accord with their actual spatial arrangement we shall call the "Ames transformation", and the result the "Ames image". Every model of an impossible object produces, by means of the Ames transformation, an Ames image in the form of an impossible object, although this naturally does not mean that all Ames images are impossible objects.
The majority of models are very obvious and hence less interesting. It is possible to apply certain stipulations to the Ames arrangement, however, to make it more challenging. We may thus insist that it should be as simple as possible, for example, or that it should form a closed figure, or that the arrangement itself should have an attractive geometric form, etc.
The following illustrations offer a selection of models; explanatory notes are provided in the accompanying captions.

Figure 3. Shigeo Fukuda, models of Escher's Belvedere

Figure 4. Mathieu Hamaekers pictured with an impossible cuboid; the model contains a number of curved bars.

Figure 5. Shigeo Fukuda, model of Escher's "Waterfall", photographed from an angle revealing the gaps in the model.

Figure 6. Mathieu Hamaekers, model of an impossible tri-bar; front view

Figure 7. The same model rotated through 45°

Figure 8. The same model rotated through 90°
