Приключения с невозможными фигурами
2. Таинственная коробка и другие любопытные фигуры
В данной главе мы узнаем, что существует и другие любопытные невозможные фигуры, которые дразнят воображение также сильно, как и трибар. Мы встретимся с невозможным двухбалочником, загадочной коробкой, которая, как окажется, состоит из настоящих кубиков, невозможным четырехбалочником и т.д. Мы пойдем дальше к пятибалочнику, шестибалочнику и т.д. А как насчет невозможного однобалочника?
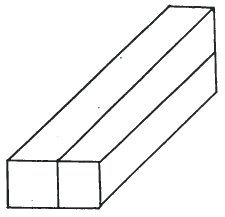
|
Невозможный двухбалочник?Ответом должно быть двойное "да". Да – возможно нарисовать невозможный двухбалочник, и да – он действительно невозможен! |
Загадочная коробка
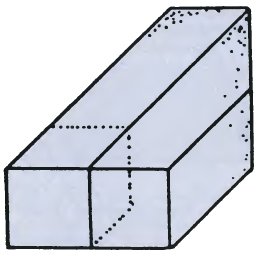
Профессор показал мне рисунок загадочной коробки, который он нарисовал днем ранее.
"Можешь ли ты сказать, сколько кубиков содержится в этой коробке?"
"Честно говоря, я не вижу здесь коробки.".
"Возможно, мне стоит показать, как я пришел к этой идее, и, возможно, это поможет тебе увидеть ее.".
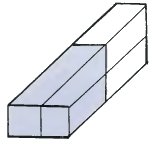
|
"Сперва я нарисовал невозможный двухбалочник, затем отпилил несколько кубиков с дальнего конца. Фигура, которая осталась, - загадочный ящик. Сколько кубиков в нем содержится?" "Я не знаю. Можешь ли ты нарисовать, как он выглядит сзади или сбоку?" |
"Конечно. Спереди он состоит из двух квадратов, расположенных горизонтально, но сзади он состоит из двух квадратов, расположенных вертикально. Он выглядит примерно так."
Профессор сделал два рисунка и обозначил их 'сзади' и 'сбоку'.
 сзади |
 сбоку |
"И все равно я не могу увидеть его, но мне кажется, в нем содержится больше четырех кубиков. Сколько же их?"
"Их ровно пять."
Профессор увидел, что я озадачен. Тогда он нарисовал невозможный трибар и перенес правую сторону треугольника дальше вправо. Так получилась новая невозможная фигура.
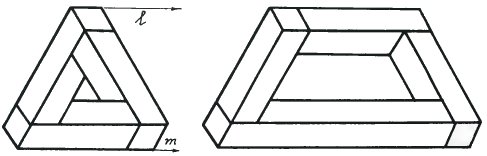
Я мог увидеть, что он создал новую невозможную фигуру - четырехбалочник, но не мог понять, какое отношение он имеет к загадочной коробке.
"И как это доказывает, что загадочная коробка содержит точно пять кубиков?"
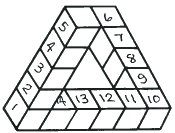
|
"Вот четырехбалочник, состоящий из 14 кубиков. Я пронумеровал их, чтобы было понятно" "Я вижу" |
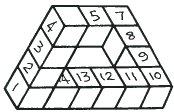
|
"Теперь давай уберем кубики 5 и 6. Образовался пробел, в который мы поместим кубик 5. Кубик 6 теперь не нужен. Таким образом, новая фигура состоит из 13 кубиков." "Я понимаю, нам не нужен один кубик." |
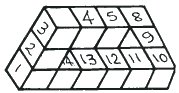
|
"Теперь я проделаю тоже самое снова. Уберем кубики 4,5,7. Образовался пробел в два кубика, в который мы поместим кубики 4 и 5. Кубик 7 больше не нужен. Новая фигура состоит из 12 кубиков" "Да, согласен." |

|
"Теперь ты можешь видеть, что если я проделаю еще раз эту операцию, то фигура превратится в невозможный двухбалочник. Я не пронумеровал кубики, но ты должен согласиться, что фигура состоит из 11 кубиков." "Да." |
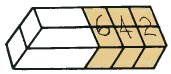
|
"Теперь давай уберем 6 кубиков справа." "И фигура, которая осталась – загадочная коробка, которая состоит из 11 - 6 = 5 кубиков. Да, теперь я в этом уверен." |
Я рад, что ты согласен со мной. Но есть и еще более маленькая коробка, которая состоит лишь из 3 кубиков, но большинство людей не могут видеть в ней коробку. А ты можешь?
Невозможный четырехбалочник
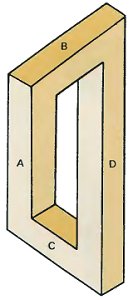
В предыдущем диалоге мы познакомились с еще одной невозможной фигурой – четырехбалочником. У него две балки расположены параллельно, а две – перпендикулярно.
Как и с трибаром, наши глаза и мозг немедленно признают эту фигуру как слитный объект типа оконной рамы, которая не может существовать.
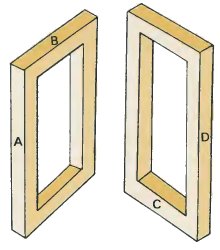
На данных рисунках изображены совершенно нормальная оконная рама с двух разных точек зрения. Давайте убедимся, что четырехбалочник является невозможной комбинацией этих двух фигур. Бруски A и B взяты с левого рисунка, а бруски C и D – с правого. Результат получился странный!
Модель невозможного четырехбалочника

На данной фотографии справа изображен объект, который выглядит как невозможный четырехбалочник, но изображение в зеркале раскрывает секрет фигуры и показывает, как она сделана. Вы можете собрать подобную модель, склеив деревянные бруски.
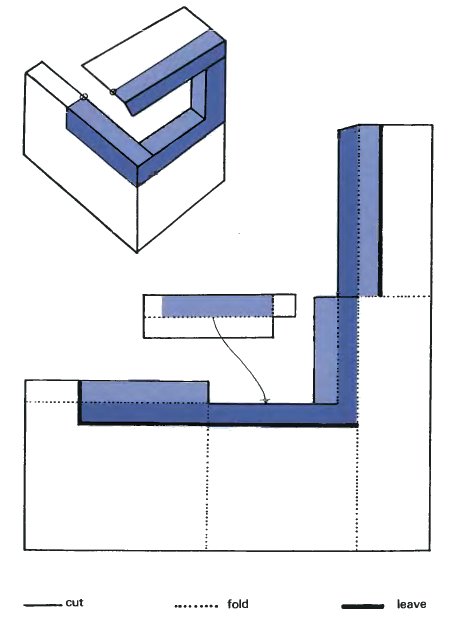
Как и с моделью со страницы 15, вам лучше всего сделать копию данного изображения и наклеить его на тонкий картон. Модель можно раскрасить для усиления иллюзии.

"Этот поразительный объект, стоящий в жаркой пустыне, построен давным давно неизвестной цивилизацией"
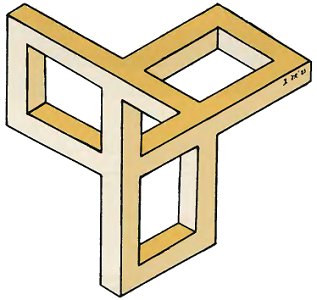
Где кончается реальность и начинается невозможность?

Странные комнаты в далеких дворцах.
Реальные углы и невозможные рамки
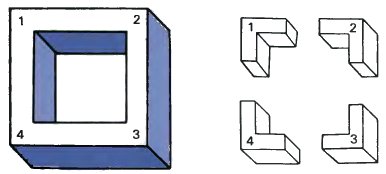
На рисунке слева изображена рамка, которая находится левее и выше относительно точки обзора. Мы можем сказать, где она находится, так как мы можем использовать подсказки, задаваемые формой углов фигуры. Все четыре угла разные, и можем убедиться насколько они разные, нарисовав их отдельно друг от друга. На втором рисунке изображены четыре типа углов, на этот раз без теней. Пронумеруем их (1, 2, 3, 4)
Эти углы можно использовать создания других четырехбылочников. Давайте начнем с фигуры с углами (1, 1, 1, 1), которая представляет собой реальный четырехбалочник, обозреваемых с точки, находящейся напротив рамки на очень малом расстоянии.
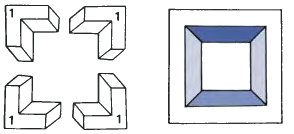
Ниже представлены четырехбалочники (1, 2, 1, 2), (4, 4, 4, 4), (4, 1, 4, 1). Все они представляют собой невозможные фигуры с разными видами невозможности.
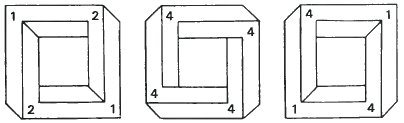
Достаточно интересно поэкспериментировать с другими комбинациями. Будут ли четырехбалочники возможными или нет?
Невозожные многобалочники (мультибары)
Не вызывает проблем развить данную идею дальше для создания невозможных фигур с количеством углов больше четырех. Назовем эти фигуры "невозможными мультибарами". Было бы разумно полагать, что могли бы построить невозможные фигуры еще более интересные и более любопытные, чем те, с которыми мы встречались ранее. Однако это нет. Для этого есть две причины.
- Изображение, нарисованное на бумаге, которое воспринимается наиболее сильно, - это рисунок с прямыми углами. Главная особенность невозможных трибара и четырехбалочника в том, что кажется, что бруски в них соединяются под прямыми углами. Углы, под которыми соединяются бруски в мультибарах, больше 90°, и чем больше угол, тем меньшее влияние он оказывает на наш мозг.
- Сложность. Чем больше линий и брусков на рисунке, тем меньше противоречий может быть замечено.
Для рисования невозможных мультибаров мы можем воспользоваться тем же методом, который мы использовали для экспериментов по совмещению углов разного типа в четырехбалочнике.
Невозможный пятибалочник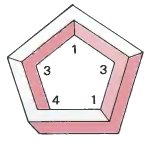 Номера углов - (1, 3, 1, 4, 3) |
Невозможный шестибалочник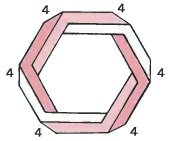 Номера углов - (4, 4, 4, 4, 4, 4) |
Невозможный бесконечно-балочник?
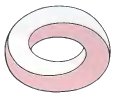
Также как круг может быть представлен как многоугольник с бесконечным количеством сторон, мы можем создать круглую невозможную фигуру. Или на самом деле на самом деле округлый двухбалочник, который можем уписать как (4, 4)?
Эта невозможная фигура присутствует на нескольких прекрасных картинах Сандро дель Прете. Вы также можете увидеть ее в невозможных алфавитах, где использование скругленных фигур очень полезно.
Невозможные однобалочники (монобары)
Для некоторых это будет сюрпризом, но невозможные монобары (или однобалочники) существуют. Однако, это так, и ниже представлены два примера.


Вполне вероятно, что вы найдете оба эти рисунки довольно разочаровывающими. Глаз вряд ли обнаружат что-то подозрительное и готов интерпретировать как рисунки простых брусков, у которых края спилены под наклоном. Но посмотрите внимательно, и вы увидите обе фигуры на самом деле невозможные монобары.
Ниже представлена более интересная версия, созданная Зеноном Кульпой. Мы видим, что слева два бруска, а справа – один. Кажется, что второй брусок почти полностью состоит из первого бруска и его тени. Так, что здесь нет второго бруска вообще.
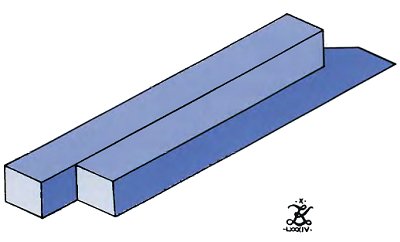
Наверное, мы должны назвать их "полтора бруска".
Вход через закрытую дверь
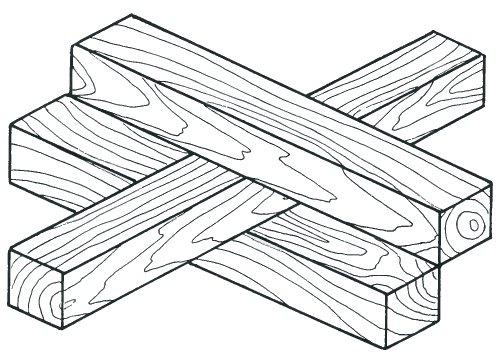
Этой гениальной невозможной фигуре удается совмещать три области, цепляющие взгляд. Слева и справа два бруска касаются краями друг друга. Третий брусок в центре проходит между ними. Тем не менее, между первыми двумя брусками нет зазора. Сказка сбылась. Можно войти сквозь закрытую дверь!
