Приключения с невозможными фигурами
4. Инверсия восприятия
Давайте отвлечемся немного от поиска новых видов невозможных фигур и исследуем феномен, называемый инверсией восприятия. Существует семейство фигур, которые наши глаза и мозг могут интерпретировать двумя (или более) способами и затем переключаться между ними.
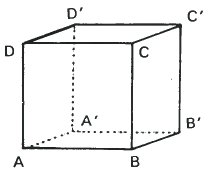 A ближе, чем A' |
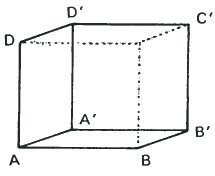 A' ближе, чем A |
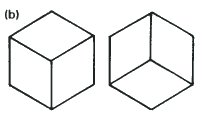
Данные два наброска куба имеют одинаковый размер, положение и обозначения. Они отличаются только тем, что одни линии в них сплошные, а другие – пунктирные. В результате, слева мы видим куб, который расположен левее и ниже нашей точки обзора, в то время как куб справа – правее и выше.
Куб Некера
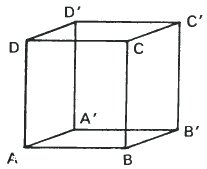
Третий куб имеет тот же размер, расположение и обозначени, но все его 12 линий нарисованы одинаково. Такая фигура называется Кубом Некера (Necker Cube). Как мы смотрим на него – сверху или снизу? Согласны ли вы, что может быть и так и так? Это двойственная фигура. Если вам сложно переключаться между двумя возможными точками обзора, посмотрите внимательно на два рисунка выше. Явление переключения между двумя интерпретациями одной и той же фигуры называется инверсией восприятия.
Когда мы смотрим внимательно на куб Некера и переключаемся между двумя интерпретациями, интересно, что происходит с отдельными линиями и плоскостями фигуры. Они не все меняются одинаковым образом. Например, линия DD' меняет ориентацию в пространстве, так как точки D и D' меняются местами, но линия AD остается параллельной самой себе. Линия AD меняет свое положение, но не ориентацию, в то время как линия DD' меняет и положение и ориентацию. Также стоит исследовать, что происходит с линией BB' и плоскостями ABCD и BB'C'C в момент инверсии восприятия.
Изменение ориентации линий куба Некера во многом зависит от точки зрения, относительно которой он изображен.
|
|
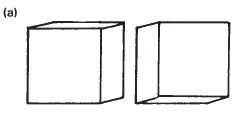
На рисунке слева угол изменения ориентации при переключении между двумя позициями очень мал. На рисунке справа угол изменения ориентации самый большой из возможных.
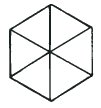
Куб Некера с наибольшим углом изменения ориентации является комбинацией обоих фигур с рисунка (b). Их комбинация образовывает правильный шестиугольник, в котором центр куба находится точно за точкой A в обоих случаях инверсии восприятия. Мы даже можем подсчитать, на какой угол он вращается при этом. Давайте проведем небольшой эксперимент с двумя игральными костями.
|
|
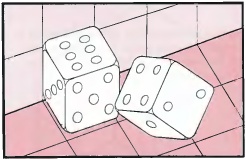
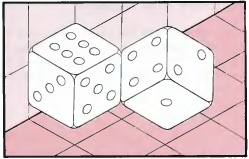
Данные рисунки игральных костей одной и той же конфигурации, изображенных с двух разных точек зрения, очень близки идее инверсии восприятия. На рисунке слева изображены два кубика, которые касаются друг друга в одной точке. Однако, на рисунке справа выбрана точка зрения так, чтобы их стороны стали параллельны. Также кубик справа выглядит вогнутым или даже вывернутым наизнанку. Интересно поэкспериментировать с двумя настоящими кубиками для достижения такого эффекта.
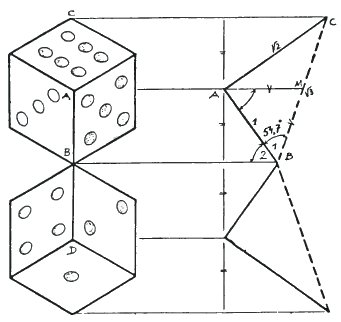
Чтобы вычислить угол, под которым стороны кубиков стыкуются друг с другом, создавая данный эффект, лучше всего переместить правый кубик вниз, чтобы его верхний угол находился в точке B, не поворачивая его. Тогда угол ABD вдвое больше угла ABC. По данному сечения мы можем рассчитать, что угол ABC равно 54.1°. Следовательно угол ABD равен 109.5°.
Выпуклость и вогнутость
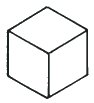
Когда мы смотрим на куб Некера, мы принимаем соглашение, которое позволяет нам смотреть внутрь куба на ребра, которые находятся позади. Давайте уберем эти скрытие ребра и оставим только те 9, которые могут быть видны на обычном кубе. Это можно сделать двумя способами, но оба они будут двусмысленными.
|
Выпуклость |
|
| 1. Это куб, видимый сверху | 2. Это куб видимый снизу | |

|
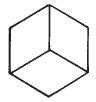
Вогнутость |

|
| 3. Это внутренние грани куба, видимые снизу | 4. Это три внутренние грани куба, видимые сверху |
Большинство людей видят выпуклую форму и испытывают некоторые трудности в видении обратной формы. Чтобы облегчить восприятие необходимо добавить визуальных указателей.
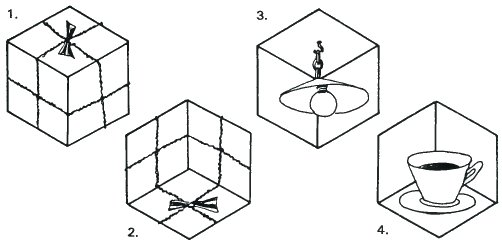
Данные четыре рисунка показывают, насколько проще принять, что форма куба выпуклая или вогнутая, когда добавлены другие детали и визуальные подсказки.
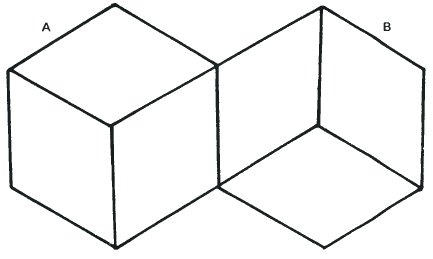
Данный рисунок представляет собой более абстрактную форму рисунка игральных костей со страницы 40 – фигуры, созданной из двух версий куба, соединенных друг с другом по одному ребру. Так как кубы A и B могут быть как выпуклыми, так и вогнутыми, у нас есть четыре варианта трактовки рисунка.
- A – вогнутый и B – вогнутый
- A – вогнутый и B – выпуклый
- A – выпуклый и B – вогнутый
- A – выпуклый и B – выпуклый
Мы задаемся следующими вопросами
- Какая из интерпретаций видима первой?
- Какие из инверсий видятся спонтанно, а какие с трудом?
- Когда ориентаций одного половины зафиксирована, просто ли перенести ее на другую половину? Правда ли что, что интерпретации 1 и 4 самые легкие для восприятия?
Лично я очень легко вижу интерпретацию 4. Для меня выпуклая форма доминирует. Далее я вижу интерпретации 2 и 3, и с очень большим трудом я вижу интерпретацию 1. Может быть, вы обнаружили, что на странице 40 точки на игральных костях делают любую интерпретацию кроме четвертой сложной для восприятия, несмотря на проблемы с неожиданной ориентацией.
Конфликт двух ориентаций
В этой главе мне не упоминали про невозможные фигуры. Каждый из двух видов куба Некера исключает второй, и, таким образом, мы имеет два альтернативных вида, а не невозможность. Давайте спросим себя, возможно ли объединить два вида таким образом, чтобы получить невозможную фигуру. Можем ли мы добавить деталей к рисунку, которые усилят один вид на одной плоскости, и другой вид на другой плоскости.
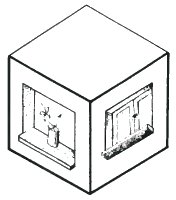
Данная фигура является попыткой объединить виды. Если мы сконцентрируемся на левой стороне, форма окна усиливает выпуклую ориентация, в то время как правая часть пытается усилить вогнутую. Однако я думаю, вы согласитесь, что этого недостаточно, чтобы утвердить фигуру в качестве стабильной невозможной фигуры.
Центральная часть картины Эшера "Выпуклость и вогнутость" показана имеет одинаковую конструкцию слева и справа, но показана с двух противоположных точек зрения. Не беря во внимание, что это картина, мы не не можем воспринимать ее как стабильную невозможную фигуру. Интерпретация Эшера должна была заставить нас испытать инверсию при движения слева направо по рисунку. "Выпуклость и вогнутость" заставляет нас испытывать инверсию как движение, а не как статический и стабильный неразрешимый конфликт.
Картина Эшера 'Куб с планками' (1957) демонстрирует ту же проблему.

Центральная часть литографии Эшера 'Выпуклость и вогнутость' (1955).

Мы впервые встретились с данной фигуру на странице 34, когда искали невозможный однобалочник. Хотя, это на самом деле невозможный однобалочник, глаз все равно продолжает рассматривать его как реальный брусок со скошенными краями. Даже если мы отрежем по кубику с каждого конца и покажем, что они имеют разную ориентацию, большинство людей продолжат считать данный факт неубедительным.
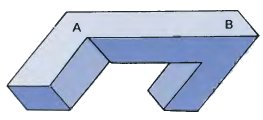
Однако, положение может быть улучшено, если мы добавим по кубику с каждого конца. Данная фигура показывает результат такого добавления. На мой взгляд – это настоящая невозможная фигура. Осмотр фигуры от точки A к точке B вынуждает нас сменить ориентацию и принять ее. Фигура невозможная, а также стабильна и убедительна в каждой точке.
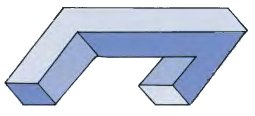
Проход взглядом дальше вызывает второе изменение ориентации.
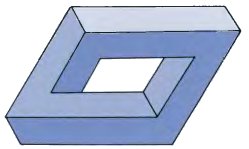
В завершение, мы можем создать замкнутую рамку, подобную той, с которой мы встречались в главе 2.
Таким образом, есть возможность придумывать стабильные фигуры, которые вынуждают нас принимать противоречивые ориентации.
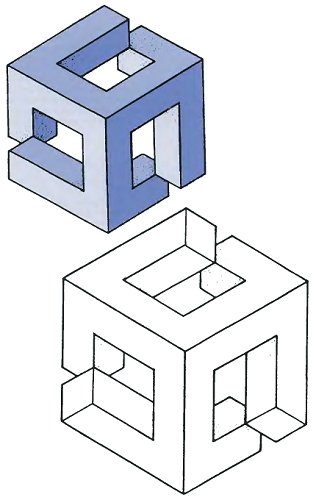
Обе фигуры на следующей странице вызывает противоречивые изменения восприятия ориентации. Верхний рисунок – невозможная фигура. Второй рисунок показывает, как могут быть модифицированы концы брусков, чтобы еще усилить странность фигуры. Обратите внимание, что такая модификация также сформировала фигуры квадратов в центрах всех трех сторон фигуры.
Фигура Тьери (The Thiéry-Figure)
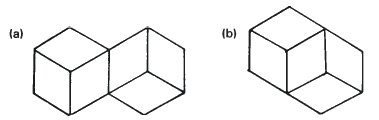
На странице 43 мы соединили два куба вместе так, чтобы они имели одно общее ребро и открыли для себя богатый источник фигур для исследований. Теперь мы сблизим их еще больше, чтобы они имели общую грань. Это показано на рисунке (b). Данная фигура была придумана А. Тьери в конце прошлого столетия (прим. переводчика: имеется в виду XIX век). Это не невозможная фигура.
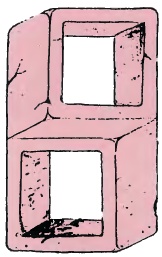
Мы можем провести исследования в отношении выпуклости и вогнутости фигуры, как мы это делали для фигуры (a). Но есть еще кое-что, что надо открыть. Во-первых, фигура весьма стабильна. Посмотрите на рисунок слева. Это весьма примечательно тем, что предполагает, что между нестабильными инверсными фигурами и стабильными невозможными фигурами существует еще один класс фигур.
Множество художников использовали фигуру Тьери в качестве основы для создания иллюзий, которые выглядят очень стабильными. В частности, Тсунео Таниучи (Tsuneo Taniuchi) разработал странный двойственный алфавит, символы H, S и T из которого представлены ниже.
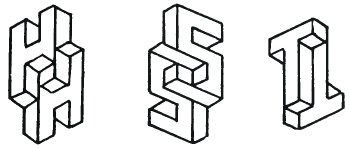
Полная версия алфавита была опубликована в сентабря 1983 года в Интернациональном Журнале Типографики (International Journal of Typographics) (Vol 10 No 3) в статье 'Upper and Lower Case'.
Любопытная модель
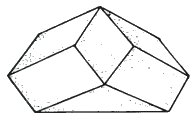
Представляет интерес создать любопытную и малоизвестную модель, предложенную мне профессором J.B. Deregowski. Фигура представляет собой нечто подобное усеченной пирамиде, которая не является ни невозможной ни двойственной, но если ее держать особыми образом, она будет выглядеть совершенно отлично от своей действительной формы. Поверните вашу модель так, чтобы минимизировать количество граней, видимых в один и тот же момент.
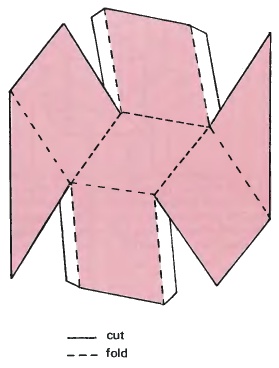
Сделайте копию данной развертки и склейте ее. Она будет без основания, но этого достаточно. Вы можете приклеить к фигуре основание для придания ей большей жесткости. Нарисуйте толстые черные линии по всем сгибам фигуры.
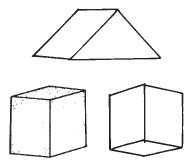
|

|
|
| Три возможных вида модели. | Фотография модели и ее отражение в зеркале. |
Это правильная установка модели перед зеркалом для получения эффекта с фотографии. Улучшает или наоборот ухудшает иллюзию раскрашивание граней модели?
