Расчет площади полной поверхности мультибаров
Автор - Кристина Юсупова (uko2304@mail.ru)
Статья из научно-исследовательской работы "Изучение мира оптических иллюзий с точки зрения математики.
Достижения в исследовании невозможных фигур",
конференция "Наше Подмосковье", номинация "Научный прорыв", 2013 г.
В математике нам известны многие способы расчета площадей поверхности различных фигур. Я чаще всего использую два из них: расчет площади фигуры по уже известным параметрам (длинам сторон, градусным мерам углов, высот), т.е. по тому, что требует формула по нахождению площади и расчет площади фигуры по формуле Пика (по целочисленным точкам внутри и на границе фигуры).
Формула Пика имеет следующий вид: В + Г/2 – 1 = S, где В – число целочисленных точек внутри фигуры, Г – число точек на границе фигуры.
На рис. 1 мы видим отмеченные разними цветами точки внутри и на границе фигуры. Согласно формуле для этой фигуры площадь будет равна: 7 + 8/2 – 1 = 10, S=10 (рис. 1).
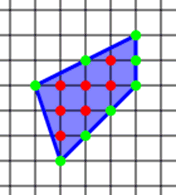
Рис. 1
Таким образом, используя эти два математических способа по нахождению площади поверхности фигур, можно рассчитать площадь поверхности мультибаров и вывести единую формулу расчета площади для этого класса невозможных фигур.
Начнем с нахождения площади поверхности объекта, пользуясь стандартными математическими формулами площадей фигур. На рис. 2 изображен трибар. Для того чтобы правильно найти площадь поверхности трибара, я разбила его грани на две части (пунктиром обозначены линии разбиения): получила, что каждая грань невозможного треугольника состоит из параллелограмма и трапеции. Отсюда, зная число граней у трибара, мы можем рассчитать площадь его поверхности, используя формулы площадей трапеции и параллелограмма.
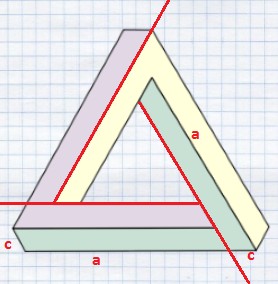
Рис. 2
Пусть сторона (длина бруска) трибара будет равна а, а ширина бруска – с. Учитывая, что бруски, составляющие конструкцию треугольника равны, то площадь поверхности мультибара будет равна сумме площадей частей грани фигуры, на которые ее разбили, умноженной на число граней мультибара.
Площадь заштрихованной трапеции равна S = (a+a-c)·c/2 = (2ac-c2)/2. Площадь параллелограмма этой же грани равна S = a·c. Получаем, что площадь одной грани S = ac+ac-c2/2 = 2ac-c2/2. Так как у мультибара 6 граней, то полная площадь его поверхности будет равна S = (2ac-c2/2)·6.
Таким образом, удалось вывести формулу площади поверхности невозможного треугольника. Отсюда мы можем вывести общую формулу площади поверхности, применимую к простым однокомпонентным мультибарам: S = (2ac-c2/2)·2n, где n - это число углов мультибара (число граней Г = 2·n). Получаем конечную формулу вида:
S = n·c·(4a-c)
Теперь обратимся к другому способу нахождения площади фигуры, формуле Пика. Напомним, что формула выглядит так: В+Г/2-1 = S, где В – это целочисленные точки внутри фигуры, а Г – на границе. Попробуем применить эту формулу к мультибарам. Одним из важнейших плюсов этой формулы является то, что она применима к объектам любой формы, поэтому разбивать грани невозможных объектов нам не придется.
На рис. 3 мы видим изображение трибара, на котором вертикальными и горизонтальными линиями образованы целочисленные точки внутри фигуры. Рассмотрим одну грань объекта: В=30, Г=27. Площадь по формуле: S = В+Г/2-1 = 30+13.5-1 = 42.5. А формула будет иметь вид: S = (В+Г/2-1)·2n, где n – число углов мультибара.
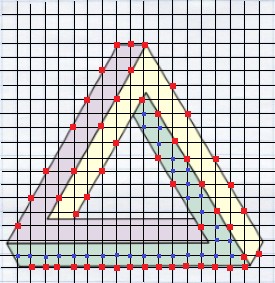
Рис. 3
Стоит заметить, что мультибары мы рассматриваем как невозможные трехмерные объекты, а не двумерные рисунки, поэтому мы учитываем при подсчетах и скрытые от нас грани этих фигур.
Выведенные формулы можно применять в простейших задачах по нахождению площади поверхности мультибаров.
Задача N1. Найдите площадь поверхности 5-угольного мультибара с площадью сечения его бруска равной 36 см2 и длиной этого бруска равной 12 см.
Решение: поперечным сечением бруска, составляющего конструкцию невозможного объекта, является квадрат, площадь которого рассчитывается по формуле: S = a2 = 36 см2. Отсюда следует, что а = 6 см. Площадь поверхности мультибара тогда равна S = n·c·(4a-c) = 5·6·(48-6) = 42·30 = 1260 см2
Ответ: 1260 см2
Задача N2. Известно, что брусок 6-угольного мультибара имеет ширину 4 мм, а длину 16 мм. Найдите полную площадь поверхности мультибара двумя способами и сравните полученные значения.
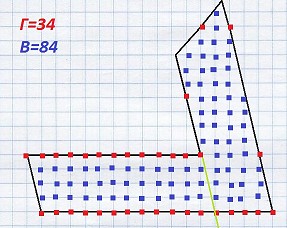
Рис. 4
Решение: 1) Найдем площадь мультибара по формуле S = n·c·(4a-c) = 6·4·(54-4) = 24·50 = 1200 мм2. 2) Найдем площадь мультибара по формуле Пика, сделав чертеж одной грани фигуры (рис. 4). На границе грани насчитано 34 точки, внутри – 84. По формуле получаем площадь одной грани мультибара: S = 84+17-1 = 100 мм2. Так как у мультибара 6 углов, то граней у него будет 12, тогда площадь полной поверхности данного объекта будет равна S = 12·100 = 1200 мм2. S0 = S (по формуле Пика).
Ответ: 1200 мм2
Мы видим, что эти формулы позволяют решать пока простейшие задачи по нахождению какого-либо параметра мультибаров. Эти задачи по виду и сложности подобны задачам стереометрии с использованием различных элементарных формул. Можно сделать вывод, что мультибары обладают определенными закономерностями в строении, которые поддаются расчетам, и исследования свойств этих фигур могут продолжаться бесконечно долго. К ряду уже известных фактов о мультибарах: соответствие их конструкции с тривиальным соединением кос, расчет площади их поверхности по выведенной формуле, решение мультибаров по формуле расчета характеристики Х, однозначно добавятся и новые открытия.
