Adventures with Impossible Figures

2. The Mysterious Box and Other Curious Figures

In this chapter we shall discover that there are other curious impossible figures which tease the imagination just as wickedly as the tri-bar. We shall meet the impossible two-bar, a mysterious box which seems to contain real cubes, the impossible four-bar and so on. Can we carry this ever onwards to the five-bar, six-bar etc? And what about the impossible one-bar?

The Impossible Two-bar? The answer must be a double 'yes'. Yes, it is possible to draw an impossible two-bar and yes, it really is impossible!

The Mysterious Box

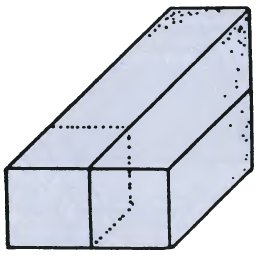
The Professor showed me a drawing of a mysterious box which he had made the previous day.

"Can you tell me how many cubes this box will hold?"

"To be honest I do not see it as a box at all".

"Perhaps, I can show you how I got the idea and perhaps that will heIp you to see it".

"First I drew an impossible two-bar and then sawed off some cubes from the far end. The shape which remains is the mysterious box. How many cubes does it contain?" "I don't know. Could you draw how it looks from the back and the side for me?"

"Of course. The front is made up of two square: horizontally, but the back is two squares vertically. It looks like this."

The professor made two drawings and marked them 'back' and 'side'.

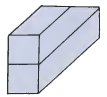back

side

"I still cannot really see it, but I think there are more than four cubes. How many are there?"

"There are exactly five."

The professor could see that I was confused. He then drew an impossible tri-bar and moved the right hand bar further to the right. This made a new impossible figure.

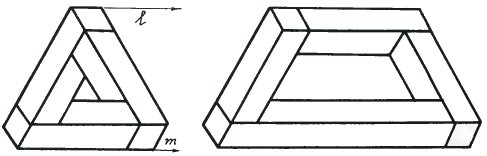
I could see that he had created a new impossible figure, a four-bar, but could not understand what it had to do with the mysterious box.

"How does that prove that your mysterious box contains five cubes exactly?"

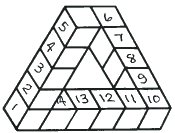
	"Here is a four-bar which contains 14 cubes. I have numbered them to make it clear" "Yes I can see that."
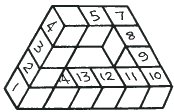
	"Let us now remove cubes 5 and 6. This leaves a space into which we can put cube 5. Cube 6 is not wanted. This new shape needs 13 cubes." "Yes, I understand, we need one cube less."
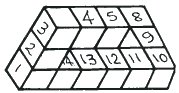
	"Right I'll do the same again. Let us remove cubes 4,5,7. This leaves two spaces into which we can put cubes 4 and 5. Cube 7 is not wanted. This new shape needs 12 cubes." "Yes, agreed."
	"Now you can see that if I go one stage further, the shape becomes an impossible two-bar. I haven't numbered it, but you must agree that it contains 11 cubes." "Yes."
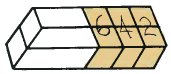
	"Now take away six cubes from the right." "And the shape which remains is your mysterious box, and it contains 11 - 6 = 5 cubes. Yes, at last I am convinced."

"I'm glad I have managed to convince you. There is an even smaller box which contains only 3 cubes, but most people cannot see it as a box at all." Can you?

The Impossible Four-bar

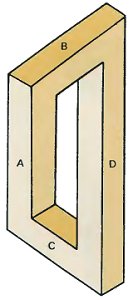
In the previous discussion we made acquaintance with a further impossible figure - the four-bar. It has two parallel bars and two which appear to cross each other perpendicularily.

As with the impossible tri-bar, the eye-brain immediately accepts it as a solid object - a kind of window frame which we know cannot exist. But which we cannot easily reject.

These diagrams show a perfectly normal window frame seen from two different directions. We can now see that the four-bar is an impossible combination of them both. Bars A and B are taken from the left diagram. Bars C and D from the right one. The result is confusion!

A Model of an Impossible Four-bar

This photograph shows on the right an object which appears to be an impossible four-bar, but the image in the mirror gives the secret away and shows how it was set up. You could make a model like this by glueing eight pieces of wood together or you could make the model opposite part, of which is an impossible four-bar.

As for the model on page 15, it is best to take a photocopy of this page and then glue it to thin card. You can use colour to strengthen the illusion.

"This wondrous object, standing fat out in the desert, and built long ago by an unknown civilization........"

Where does reality end and impossibility begin?

Strange rooms in palaces far away.

Real Corners and Impossible Frames

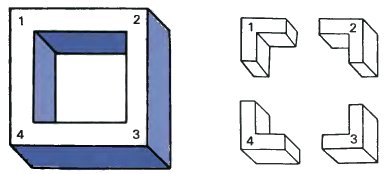
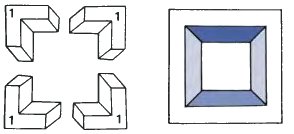
The drawing on the left represents a solid frame which is above and to the left of our view point. We can tell where it is, because we can make use of the clues given by the shapes of the corners. All four corners are different and we can easily see how different they are by drawing them separately. Drawing (b) shows the four types, which we number (1, 2, 3, 4), this time without shading.

It is possible to use these corners to make up other four-bars. Let us start with (1, 1, 1, 1), which gives us a real four-bar seen from a viewpoint which is close to the frame and straight in front of it.

Below are the four-bars (1, 2, 1, 2), (4, 4, 4, 4), (4, 1, 4, 1). All are impossible figures, with different kinds of impossibility.

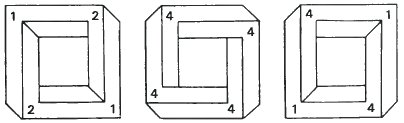
It is interesting to experiment with other combinations. Are the resulting four-bars real or impossible?

Impossible Multi-bars

There is no problem in developing this idea further to generate impossible figures which have more than four bars. We can call them 'Impossible multi-bars'. It would be reasonable to hope that one might be able to construct impossible figures which are even more interesting and more curious than those we have met so far. However that is not the case. There are two main reasons.

1. The image on paper which is perceived most strongly is that of a right-angled corner. The strength of the tri-bar and the four-bar is that all the corners appear to be right-angles. The angles at which the bars of multi-bars meet is greater than 90° and the greater the angle the less secure is the grip on the mind.
2. Complexity. The more lines and bars there are in the drawing the less the contradictions may be noticed.

To draw impossible multi-bars we can use the same method as we used for the four-bar and experiment by joining corners of different types.

An impossible five-bar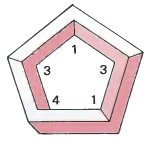 This impossible figures is (1, 3, 1, 4, 3)

An impossible six-bar This impossible figures is (4, 4, 4, 4, 4, 4)

An Impossible Infinity Bar ?

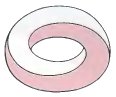
Just as a circle can be seen as a polygon with an infinity of sides, so we can create a rounded impossible figure. Or is it really a rounded two-bar which we could describe as (4.4)?

This impossible figure has been worked into several beautiful pictures by Sandro de Prete. You can also see it in impossible alphabets where the rounded shape comes in very useful.

Impossible Mono-bars

Most people find it surprising that impossible mono-bars can exist at all. However, they can, and here are two examples.

It is likely that you will find both of these drawings rather disappointing. Most people do. The eye hardly detects anything suspicious and is willing to interpret both drawings simply as bars which have been sawn off at a slant. Look carefully though, and you will see that both are indeed impossible mono-bars.

Below is a much more interesting version which was created by Zenon Kulpa. On the left it seems to be two distinct bars. On the right there is only one. It seems that the second bar is almost entirely created out of the first and its shadow. So there is no second beam at all.

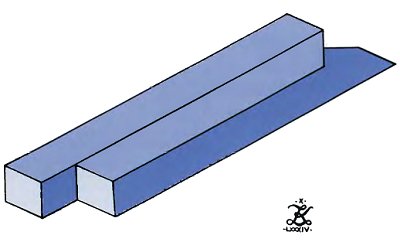
Perhaps we should call it 'a beam and a half'.

Enter Through Closed Doors

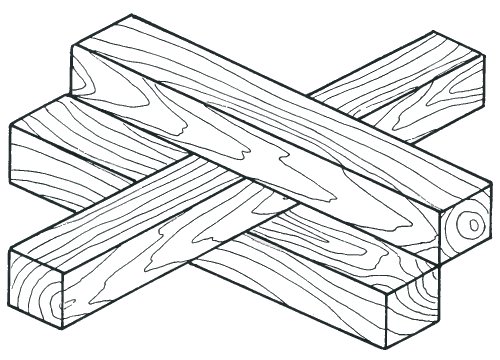
This ingenious impossible figure manages to combine three regions, each strongly acceptable to the eye. On the left and right two beams appear to touch along an edge. In the centre a third beam passes between the other two. Yet they are the same two beams which have no space between them. A fairy-tale has come true. One can enter through closed doors!