Adventures with Impossible Figures

4. Perceptual inversion

Let us leave our search for further kinds of impossible figures for the moment and investigate a closely related phenomenon called perceptual inversion. There exists a family of figures which the eye-brain combination can interpret in two or more ways and then be persuaded to switch between them.

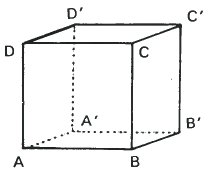A is nearer than A'

A' is nearer than A

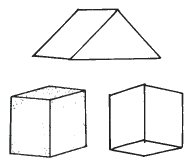
These two sketches of a cube are identical in size, position and lettering. They differ in that certain lines are strengthened or weakened. The result is that on the left we see a cube which is below and to the left of our viewpoint whereas on the right we see a cube which is above and to the right. There is no ambiguity.

The Necker Cube

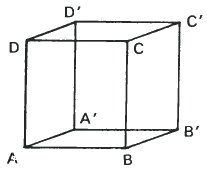
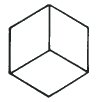
This third cube is identical in size, position and lettering but all 12 lines are drawn with equal emphasis. It is called "The Necker Cube". Are we looking at it from above or from below? Do you agree that it could be either? It is an ambiguous figure. If you find it hard to switch between the two possible viewpoints, then look carefully at the two sketches above. The phenomenon of switching between the two interpretations is called perceptual inversion.

When we look carefully at the Necker Cube and are able to switch at will between the two interpretations, it is interesting to see what happens to particular lines and planes. They do not all change in the same way. For instance DD’ changes in orientation is space as D and D' change places but AD remains parallel to itself. AD changes in position, but not in orientation, but DD’ changes in both position and orientation. It is worth investigating what happens to BB' and to the planes ABCD and BB'C'C as the perceptual inversion takes place.

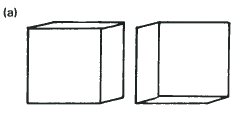
The change in orientation of the lines in the Necker Cube depends very much on the viewpoint from which the cube is drawn.

The angle of change is very small when the cube is drawn so that it inverts between the two positions on the left. On the right the angle is as great as it can be. The drawing on the right compares with the top right of the dice pictures opposite.

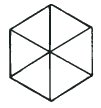
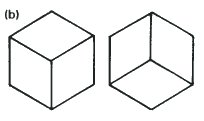
The Necker Cube with the greatest angle of change is the one which is a combination of the two drawings in (b). They combine to give a hexagon and the centre of the cube is directly behind A in both states of inversion. We can even calculate the angle through which it rotates. Let us now consider a little experiment with two cubical dice.

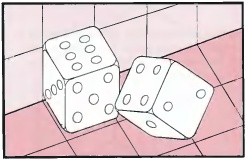
These drawings are of the same configuration of two dice but from two different view-points and they closely parallel the ideas of perceptual inversion. The drawing on the left shows that the two cubes actually touch at a single point. However, the drawing on the right shows that choosing a particular view-point can make the edges appear parallel. Also the right cube appears to lean backwards or even appears to be inverted. It is interesting to experiment with two cubes to obtain this effect.

To calculate the angle which the edges make with each other to create this effect, it is best to move the right hand cube down so that its top corner corresponds with B, not turning or twisting it as you do so. Then the angle ABD is twice the angle ABC. From the section on the right we can calculate that ABC is 54.7°. Hence the angle ABD is 109.5°.

Concave and Convex

When we look at a Necker Cube we are accepting a convention which allows us to see inside the cube to the edges behind. Suppose we now leave out those hidden edges and draw only the 9 edges which could be seen on a solid cube. It can be drawn either way up and in either case there is ambiguity.

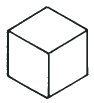
	CONVEX
1. It is a solid cube seen from above.		2. It is a solid cube seen from below.
	CONCAVE
3. It is a drawing of the 3 inside faces of a cube seen from below.		4. It is a drawing of the three inside of a cube faces seen from above.

Most people see the convex form straight away and have some difficulty in seeing the inverted form. To make it easier we need more visual signposts.

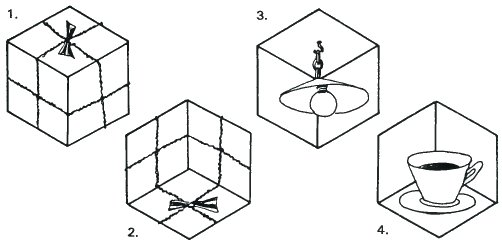
These four drawings show how much easier it is to accept that the cube shape is concave or convex, once other details and visual clues are added.

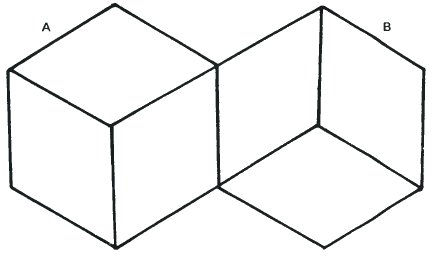
This figure is an abstraction of the dice drawing on page 40 and is also the figure created when the two versions of the cube on the page opposite slide together to share a common edge. Since either A or B can be concave or convex we have four possibilities.

1. A is concave and B is concave.
2. A is concave and B is convex.
3. A is convex and B is concave.
4. A is convex and B is convex.

We can then ask ourselves the following questions.

1. Which interpretation is seen first?
2. Which inversions will take place spontaneously and which are difficult?
3. When the orientation of one half is fixed is it easy to carry it over into the other half? Is it true that interpretations 1 and 4 are the easiest to see?

Speaking personally, I see 4 most easily. For me the convex form dominates. Next I can see 2 and 3 and only with great difficulty can I see 1. Perhaps you found on Page 40 that the spots on the dice made any interpretation except 4 very difficult in spite of the problem with the unexpected orientation.

The Conflict of Two Orientations.

In this chapter we have not so far mentioned impossible figures. Each of the two views of the Necker cube excludes the other and so we have alternative views, not impossibility. We now ask ourselves if it is possible to combine both views in some way in order to create an impossible figure. Can we add details which force one view on one plane and the other on another?

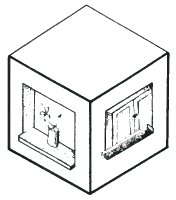
This figure shows an attempt to do this. If we concentrate on the left side the shape of the window forces a convex interpretation, whereas on the right it tries to force a concave interpretation. However, I think you will agree that it does not really seem to establish itself as a pleasingly stable impossible figure.

The central part of Escher's print 'Concave and Convex' is shown opposite and it also has a similar construction. Isolated from the print we cannot perceive it as a stable impossible figure. Escher's interpretation was to make us experience inversion in a jerky way as we pass from left to right across the drawing. 'Concave and convex' makes us experience inversion as a movement, not as a static and stable unresolved conflict.

The print 'Cube with boards' also by Escher (1957) presents the same problem.

The middle section of the print 'Concave and Convex' by Escher (1955).

We first met this figure on page 34 in the search for a convincing impossible mono-bar. Although it is indeed an impossible mono-bar, the eye is still willing to regard it as a real bar with slanting ends. Even when we cut a cube from each end and so show the different orientations, most people still find it rather unsatisfactory.

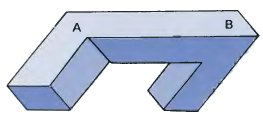
However, matters can be improved if we add to the cubes at either end. This figure shows the result. In my opinion it is a true impossible figure. Going from A to B forces us to switch orientation and then to accept it. It is impossible and yet it is stable and convincing at every point.

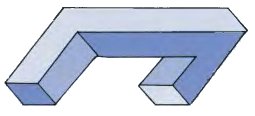
Going one stage further forces a second change of orientation.

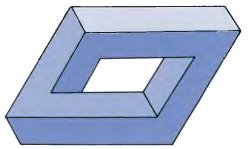
Finally we can create a closed framework rather like those in chapter 2.

So it really is possible to develop stable figures which force us to accept contradictory orientations.

Both figures on the page opposite force contradictory changes of orientation on the eye. The upper diagram is an impossible figure. The second shows how the ends of the bars can be modified to increase the strangeness. Note how it has also created squares at the centres of all three faces.

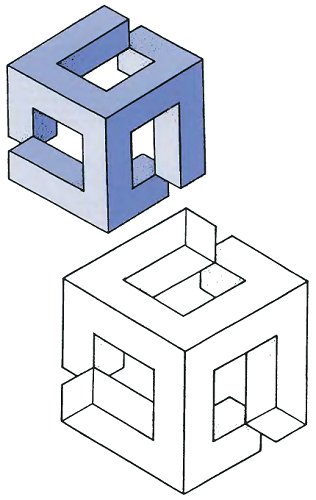
The Thiéry-Figure

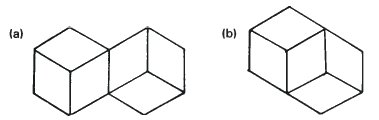
On page 43 we slid two cubes together so that they shared a common edge and obtained a rich source of figures and investigations. Now we can slide them even closer together so that they share a common face. This is shown in diagram (b). This figure was thought of by A.Thiéry at the end of the last century. It is not an impossible figure.

We could do an investigation of the concave-convex relationship as we did for figure (a). But there is more to be discovered. Firstly, it is rather stable. See the drawing on the left. This is rather remarkable because it suggests that the dividing line between unstable inversion figures and stable impossible figures is not all that great.

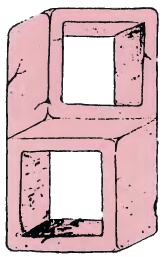
A number of artists have been used the Thiéry-Figure as a basis to generate illusions which seem remarkably stable. In particular Tsuneo Taniuchi, who designed a strange double alphabet, of which the three letters H, S and T are given below.

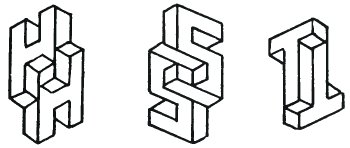
The whole alphabet was printed in 'Upper and Lower Case' Vol 10 No 3, September 1983 in the International Journal of Typographics.

A Curious Model

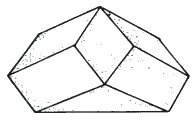
It is interesting to make this curious and little known model which was suggested to me by Professor J.B. Deregowski. It is a kind of truncated pyramid, which is neither impossible nor ambiguous, but held in certain ways it looks three-dimensional in a quite different way from its actual shape. Turn your model so as to minimise the number of faces you can see at the same time.

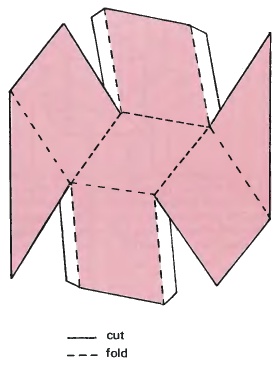
Trace or copy this plan and then make it up. Without a base it works quite well, but you might prefer to add one later to give it extra strength. Draw thick black lines along all the creases.

Here are three possible views of the model.		Here is a photograph of the model and its image in a mirror.

It is well worth holding your model in front of a mirror to reproduce the effect in the photograph. Does colouring the faces improve or reduce the illusion?