The Eye Beguiled
3. Ambiguous figures
The exterior world conveys itself to the human individual largely via the sense of sight, which comprises the eyes, the optic nerves, and the visual centre in the brain. For the sake of brevity, in the following chapters we shall refer to the sense of sight simply as the EYE. (Where eye appears in the usual, lower case, only the optical instrument is intended.)
As discussed in the preceding chapter, the vision process begins with a picture of the environment projected onto the retina via the lens. The information on the retina is highly complex. For our purposes, two categories may be distinguished: image information, based on pictographic elements which reproduce the objects present, and spatial information, composed of stereographic elements which reproduce the spatial relationships between these objects.
These two types of element generally appear together, as a simple example will illustrate. In the drawing of two fishermen on the banks of a canal (figure 1), the pictographic elements show us two human figures and a ditch or trench. The stereographic elements tell us the following: one figure is bigger than the other and partially obscures it; the figures are part dark, part light; two shadows fall behind the dark parts; the borders of the canal converge.

Figure 1
The EYE processes both the pictographic and the stereographic elements into one meaningful interpretation. In our normal environment this usually poses no difficulties, and the entire process takes place within a fraction of a second. But occasionally there is a hiccup and the process comes to a standstill; only then do we become conscious of the functioning of our EYE.
Perhaps you have also experienced an incident similar to one that occurred to me. Lying in bed one day, looking at the objects on my bedside table, I noticed something which struck me as completely foreign: a small frame with a metallic gleam on its left side only. I knew for a fact that I possessed no such frame, so one couldn't be standing there. I didn't move, but continued to look at it patiently, hoping to penetrate the mystery. Suddenly I recognized my lighter on the left, standing upright, and on the right a glass, partially obscured by a postcard. This made a lot more sense, and I subsequently found it quite hard to recreate in my mind's eye my original impression of a frame.
There are other instances when the EYE offers us two (and in some cases even more) equally valid interpretations of a particular object configuration. It should be noted, however, that such interpretations derive not from our own mental reflection upon what we are seeing, but directly from the EYE itself. We become aware of an ambiguity because we see first one interpretation, then another, and then, a few seconds later, the first again, and so on. We are dealing here with a process which we ourselves can neither control nor stop, since it takes place automatically. In such cases we speak of ambiguous retinal images and - where these are triggered by a pictorial figure - of ambiguous figures. Their ambiguity can be pictographic or stereographic in nature. Although this book is primarily concerned with stereographic (spatial) ambiguities, I would not wish to deprive the reader of some of the particularly entertaining ambiguities which can arise in the pictographic field. For this reason, and to help clarify the distinction between the two fields, I have included a number of examples below.
Pictographic ambiguity

Figure 2. W.E. Hill, "My wife and my mother-in-law"
Almost everyone will have come across the phenomenon of pictographic ambiguity, especially in the form of "Freudian" pictures. A particularly good example is My wife and my mother-in-law (fig. 2), published in 1915 by the cartoonist W.E. Hill, which offers a finely-balanced choice of interpretations by omitting all extraneous details. See whom you recognize first - it can be a hard task even for psychologists! A few years later, Jack Botwinick produced a pendant picture, My husband and my father-in-law (fig. 3). Many such images have been invented over the years; the Eskimo-Indian (fig. 4) and Duck-Rabbit (fig. 5) are particularly wellknown.

Figure 3. Jack Botwinick, "My husband and my father-in-law"

Figure 4. Eskimo-Indian

Figure 5. Duck-Rabbit
There are also ambiguous figures whose interpretation depends upon the angle from which they are seen. An extreme example in this case is the comic strip series by Gustave Verbeek which appeared in the New York Herald from 1903 to 1905.

Figure 6. Gustave Verbeek, cartoon from his Upside-down series
Each instalment must first be read and viewed normally, and then the whole thing turned upside down. Figure 6 shows Little Lady Lovekins being picked up by Rock, the giant bird; viewed upside down, the picture shows a large fish upsetting old man Muffaroo's canoe with its tail. Famous, too, are the "double images" in which the significance and function of object and background continuously alternate. In a first glance at Sandro del Prete's The window opposite (fig. 7), you will probably see no more than a vase of flowers, a wine glass, and a pair of stockings hanging out to dry.

Figure 7. Sandro del Prete, "The window opposite", pencil drawing
Stereographic ambiguity
The images on our retina are two-dimensional. An important function of the EYE is to reconstruct three-dimensional reality from these two-dimensional images. When we look through two eyes, the two images which fall upon our retina contain slight differences; an independent EYE programme uses these differences to calculate - with a high degree of accuracy up to a distance of fifty metres - the spatial relationships between objects and ourselves, which suggests to us a direct impression of space. But even the retinal image of one eye alone contains sufficient data with which to produce a reliable picture of three-dimensional reality. The reduction of three-dimensionality to two-dimensionality involves a fundamental ambiguity, however, as can be illustrated in a simple example. The line AB in Fig. 8a can be interpreted by the EYE in a number of ways. It can be seen, e.g., as a line of ink on the page of this book, or as a straight line in space, whereby we cannot tell whether A or B is nearer. As soon as we provide the EYE with a little more information, e. g. by incorporating the straight line AB into the drawing of a cube, the positions of A and B in space are established. In Fig. 8b, A appears nearer than B, and B lower than A; in Fig. 8c these relationships are reversed. In Fig. 8d the same straight line AB runs horizontally from the foreground way back to the horizon!
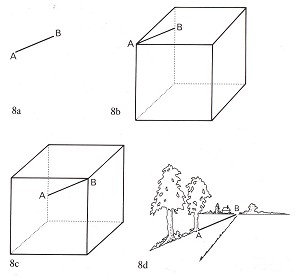
Figure 8.
A cube in which the twelve edges alone are drawn as lines (fig. 9) is called a Necker cube after L.A. Necker, the German professor of mineralogy, the first person to study stereographic ambiguity from the scientific perspective.
The Necker cube
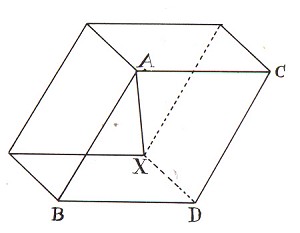
Figure 9. A Necker parallelepiped
On 24 May 1832 Professor Necker wrote a letter to Sir David Brewster, whom he had recently visited in London. The second half of the letter was devoted to what has since become famous as the Necker cube. The letter is important not just because it was the first time that a man of science had described the phenomenon of optical inversion, but also because it captures something of the astonishment of its author. It also sheds light on a typical feature of scientific practice of the times, whereby it was not yet common to work with a number of different test participants, nor to employ specially-built apparatus. Rather, the researcher made his own observations and attempted, often with very basic means, to see beyond appearances, in the hope of arriving at a conclusion within the framework of his own knowledge.
"In the case of the object to which I would like to draw your attention, we are dealing with a perceptual phenomenon in the field of optics, a phenomenon which I have observed many times when studying pictures of crystalline shapes. I am referring here to a sudden and involuntary change in the apparent position of a crystal or other three-dimensional body reproduced on a two-dimensional surface. What I mean can be more simply explained with the help of the attached illustrations. The rhombus AX is drawn in such a way that A is nearest to the viewer and X furthest away. ACBD thus represents the frontal plane, with XDC a lateral plane behind it. If you study this figure for a while, however, you will observe that the apparent position of the rhombus sometimes changes, whereby X appears to be nearest and A furthest away and plane ACBD moves behind plane XDC, giving the whole body an entirely different orientation.
For a long time I remained uncertain as to the explanation of this random and involuntary change, which I regularly encountered in various forms in books on crystallography. The only thing I was able to detect was an unusual sensation in the eye at the moment of change. To me this indicated an optical effect, and not just (as I had first thought) a mental one. Later, after thorough analysis, it seemed to me that the phenomenon was linked to the focal setting of the eye. When the point of focus on the retina (i.e. the yellow spot) is directed at A, for example, this corner is seen in sharper focus than the others. This naturally implies its being nearer and at the front, while other corners seen less clearly give the impression of lying further back.
The 'switch' occurred when the point of focus was shifted to X. Once I had discovered this solution, I was able to find three separate proofs of its correctness. First, I was able to see the object in the orientation of my choice, an orientation which I could change at will simply by shifting my focus between points A and X.
Secondly, when I concentrated on A and saw the rhombus in the correct position with A in the foreground, and then, without moving my eyes or the figure, slowly moved a concave lens between my eye and the figure from the bottom of the figure to the top, the switch took place as soon as the figure became visible through the lens. It thereby assumed the orientation in which X appeared furthest to the front. And that solely because X had replaced A at the point of focus, without any spatial adjustment of the latter.
Finally, when I looked at the figure through a hole, punched in a card with a needle, in such a way that either A or X could not be seen, the orientation of the body was determined by the corner that was Visible, whereby this corner was always the nearest. It is then impossible to see it in any other way, and thus no switch takes place.
What I have said of the corners is also true of the sides: the planes to which the line of sight or the yellow spot of the retina are directed are always seen as lying in the foreground. It is thus clear to me that this small and at first sight so puzzling phenomenon is based on the law of focus.
You will no doubt be able to draw many conclusions from the observations described here which I, in my ignorance, am unable to predict. You may use these observations according to your own discretion."
Many who have made the same experiment since Necker have come to the conclusion that this switching occurs spontaneously and independently of the point of focus. Nevertheless, Necker's original assumption - that the phenomenon occurs in conjunction with the processing of the retinal image in the brain - was correct. In the Necker cube, the EYE cannot determine whether one point (or plane) is closer or further away than another. Figure 10 shows the Necker cube, with its solid ABCD-A'B'C'D' lines, between two others illustrating its two possible interpretations. When we look at the Necker cube, we see first the figure in the centre, then the one on the right, followed shortly afterwards by the one on the left - and so on. This switching from "A-is-nearer-than-A'" to "A-is-further-away-than-A'" we call perceptual inversion: the cube in the centre is thus the inverse representation of the cube on the right, and vice versa.
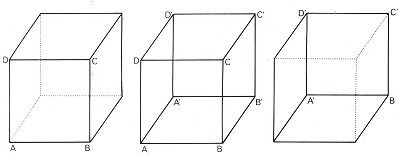
Figure 10.
However, this alternation in the relative distances of ABCD and A'B'C'D' to the viewer is not what strikes us most forcibly. Most conspicuous of all is the fact that both cubes have quite different orientations, just as Necker emphasized in his letter. Thus AD and AD' appear to intersect, although in the drawing they in fact lie parallel. We might describe the phenomenon of perceptual inversion more precisely as follows: all lines have the same orientation in the retinal image, but as soon as the interpretation switches to the inverse figure, all lines (in space) appear to change their orientation. Such changes of orientation can prove highly surprising, as we shall see. Perceptual inversion in the upper pair of dice in Figure 11 has been encouraged by the choice of angle at which the dice are shown. The drawings were based on two photographs of the same configuration of dice, but taken from different angles. The left-hand dice was placed against a wall, and squares of the same size as its sides were marked out on the wall and ground. The lower drawing makes the completely different orientations of the dice more than clear.
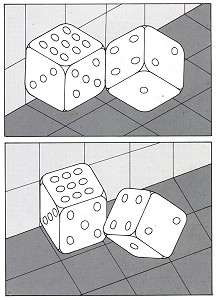
Figure 11.
The angle at which a cube is shown also determines the angle through which its sides will project after inversion. In the left-hand pair of dice in Figure 12, this angle is only small; in the right-hand pair (corresponding to the upper drawing in Figure 11), it reaches a maximum.
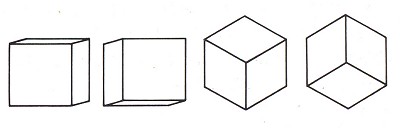
Figure 12.

Figure 13. Monika Buch, "Intersecting bars", acrylic on fibreboard, 60 X 60 cm, 1983. The impression of intersecting bars is reinforced here by the fact that the bars appear grouped at a slight angle to each other within the pictorial plane. The tautness of the composition is emphasized by the regular arrangement of the twenty-four small rhombic planes forming the ends of the bars.
Concave and convex
Although the Necker cube suggests two different geometric forms, the terms "concave" and "convex" can be applied to neither; we can always see both the inside and the outside of the Cube at once. The situation changes when we omit from our drawing three planes which meet at or near the centre of the cube, as in dice reproduced above. We now obtain a figure which again suggests two inverse spatial bodies, but of a different nature: one convex, in which we see only the outside of the cube, and one concave, whereby we perceive only three of the planes inside the cube. Most people recognize the convex form immediately, but have difficulty seeing the concave form unless suitable subsidiary lines are added.
In his lithograph Concave and convex (fig. 14), Maurits Escher demonstrated how the viewer can be forced, by specific geometrical means, to interpret the left half of a picture as convex and the right half as concave; the transition between the two halves is thereby particularly interesting. At first sight, the building appears symmetrical: the left half is more or less the mirror image of the right, and the transition in the middle is not abrupt, but gradual and natural. And yet, as we cross the centre, we find ourselves plunging into something even worse than a bottomless abyss: everything is quite literally turned inside out. Upper side becomes underside, front becomes back. Alone in resisting this inversion are the human figures, lizards and flowerpots; these we continue to identify with palpable realities which are unknown to us in "inside-out" form. Yet they, too, must pay the toll for crossing over onto the other side: they must inhabit a world in which their topsy-turvy relationship to their surroundings is enough to make the viewer dizzy. Take the man climbing the ladder in the bottom left-hand corner: he is about to reach a landing in front of a small temple. He may wonder why the scalloped basin in the centre is empty. Then he might try to mount the steps on the right. And now the dilemma is upon him: what he took to be a flight of stairs is in fact the underside of an arch. He will suddenly find that the landing, once solid ground beneath his feet, has become a ceiling, to which he is strangely glued in defiance of all the laws of gravity. The woman with the basket will find the same happening to her. If she descends the stairs and crosses the centre. If she stays on the left-hand side of the picture, however, she will be safe.

Figure 14. M.C. Escher, "Concave and convex", lithograph, 27.5 X 33.5 cm, 1955. "Can you imagine, I spent more than a whole month brooding over this picture constantly, because my initial drafts were all far too difficult to make head or tail of." (M.C. Escher)
Most visually discomforting of all, perhaps, are the two trumpet-players located one on each side of the vertical centre line. The upper, left-hand player is looking out of a window over the groin-vaulted roof of a small temple. From his position he could feasibly climb out (or in?), drop onto the roof and jump down onto the landing. Any music played by the trumpeter lower down on the right, on the other hand, will float up to a vault above his head. This player had better dismiss any thoughts of climbing out of his window, for below him is nothing but a void. In his half of the picture, the "landing" has been inverted and lies out of sight beneath him. The emblem on the banner in the top right-hand corner of the picture neatly summarizes the content of the composition.
In allowing our eye to travel slowly from the left of the picture to the right, it is also possible to see the right-hand vault as a flight of steps - in which case the banner appears totally implausible... But let me leave you to explore for yourself the many other confounding dimensions of this intriguing print!
We frequently experience geometric ambiguity in our retinal images even where this is not intended by the original picture viewed. Studying a photograph of the moon, for example, we find after a while that the craters transform themselves into raised hillocks, despite the fact that we know them to be craters. In nature, whether an image is interpreted as "concave" or "convex" is strongly influenced by the fall of the light. Where the light comes from the left, the left-hand crater wall will have a bright exterior and a dark interior.
If we study a photograph of the moon, we assume a certain angle of light in order to recognize its craters as such. If, next to this first moon photograph, we then place the same photograph turned upside down (fig. 15), the light conditions assumed in the first will be applied to our reading of the second, whereby it is very difficult to resist an "inverted" interpretation: almost all the crater depressions in the first photograph are now read as hilly elevations in the second.

Figure 15. Photograph of the moon (left) and the same photograph printed upside down (right).
The same phenomenon can sometimes be observed simply by turning a drawing or a normal photograph upside down. This is illustrated here in the examples of a postcard of a Belgian village (fig. 16) and a detail from a picture by Escher (fig. 17), both printed upside down here.

Figure 16. Postcard of a Belgian Village, printed upside down.

Figure 17. Detail from M.C. Escher's "Town in southern Italy", 1929, printed upside down.
Even utterly normal everyday objects can suddenly assume an ambiguous dimension, particularly when we see them in silhouette or almost in silhouette.
Mach's illusory movements
A phenomenon can be observed when looking at a three-dimensional reality which does not occur in the case of two-dimensional reproductions. This can be demonstrated by means of a simple and entertaining experiment. Take a rectangular piece of paper measuring approximately 7 x 4 cm and fold it in half lengthways. Then open it out again into a V-shape (fig. 18), and stand it upright with the fold pointing away from you. Now look at it with just one eye. After a few seconds, the vertical paper inverts into the form of a long, horizontal roof. If you now turn your head to the left, to the right; up, and down, you will observe the "roof" appearing to pivot against the background. Two things are striking: first, this pivoting movement occurs contrary to our expectations; secondly, the inverse form remains stable as long as the movement continues. (The experiment can naturally also be made with the paper placed horizontally with the fold pointing upwards; the inverse form is then vertical.)

Figure 18.
We can devise many models to demonstrate this illusory movement. Paolo Barreto thought up a simple but highly effective inversion model in his Holocube (fig. 19), a composition of three concave cubes. The figure's inverse (convex) form is, however, much more stable than its actual concave geometric form; viewed at some distance, therefore, it appears as three convex cubes which, if we turn our head, seem to float strangely in space. This phenomenon, first described by Ernst Mach, also occurs spontaneously in concave images. We see such images as convex because the concave form strikes us as improbable (figs. 20 and 21). When we move, the inverse image follows us. This is particularly surprising when the image in question is the cast of another face!

Figure 19. Paolo Barreto, Holocube

Figure 20. Photograph of the small sheet-metal staircase given to M.C. Escher by Prof. Schouten. This model was the inspiration behind Escher's lithograph "Concave and convex". In drawing form it has long been known as Schroder's steps.

Figure 21. Two photographs of a concave picture by Sandro del Prete. The EYE nevertheless prefers a convex interpretation.

Figure 22. Monika Buch, "Thiéry's figure II", acrylic on fibreboard, 60 X 60 cm, 1983. The Vertical strips composing the picture are extended to fill the entire surface.
Pseudoscopy
In connection with his picture Concave and convex, Escher confided to me that although he was able to see many objects inverted with one eye, he had never managed to do so with a cat. During this same period I introduced him to the phenomenon of pseudoscopy, in which this kind of "inside-out" vision is forced upon the EYE. We can make our program for three-dimensional vision run the wrong way round by offering the left eye an image destined for the right eye, and vice versa. The same effect can be achieved, somewhat more simply, with the use of two prisms showing both eyes a mirror image.
Escher was most enthusiastic about these prisms; for a long time he carried them about with him everywhere, in order to view three-dimensional objects of all kinds in their pseudoscopic form. As he wrote to me: "Your prisms are basically a simple means of experiencing the same sort of inversion that I was trying to achieve in my picture Concave and convex. The small, white, sheet-metal staircase given to me by the mathematician Professor Schouten, and which gave rise to the picture Concave and convex, inverts as soon as you look at it through the prisms. I have mounted them between two pieces of cardboard, held together with elastic bands. They make a handy pair of 'binoculars'. I took them on a walk with me and entertained myself eg. by looking at some leaves which had fallen into a pond, and which I could suddenly turn on their heads: a 'water level' with water on top and air below, without a drop falling 'down'! The normal interchange of left and right is interesting, too. If you watch your feet moving, and try to extend your right one, it is the left foot which appears to move."
With a little care and patience, you can use Figures 23 and 24 to build your own pseudoscope, allowing you to experience illusory movements on a larger scale.
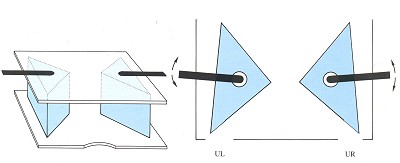
Figure 23 and 24. Perspective drawing and top view of a prismpseudoscope.
Thiéry's figure

Figure 25. Invertible illustration by Mitsumasa Anno. Several houses share a common roof and represent a variant of Thiéry's figure.
In 1895 Armand Thiéry published a detailed article on his investigations into a specific area of optical illusions. It is here that we find the first mention of the figure that now bears his name, and which has since been employed in countless variations by the artists of Op Art. The most famous such variant consists of five rhombuses with angles of 60 and 120 degrees (fig. 26). This appears to most people as a highly ambiguous figure, in which two cubes continuously and altemately assert either their concave or convex form. Thiéry was careful to conduct all his experiments under the same conditions and employed several test participants "in order to make the observations more reliable". He still fell short of the methods of modern statistics, however, since he failed to specify the arithmetical mean of his observation results, and furthermore chose his test participants for their specialist knowledge in related fields, such as experimental psychology, applied drawing, aesthetics etc. - precisely what a modern-day researcher would avoid!
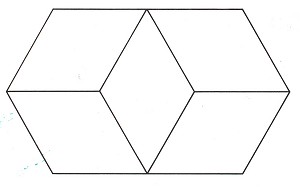
Figure 26. Thiéry's figure
Thiéry writes: "All perspective drawings reflect a specific position adopted by the eye of the artist and the viewer. Depending on the extent to which we clarify this position, different drawings can be variously interpreted. Figure (27) is an illustration of a prism seen from below, Figure (28) a prism seen from above. But these drawings become ambiguous when the two figures are combined so that the two prisms share a common face (fig. 29). When read from right to left, the figure represents a folding screen seen from above."
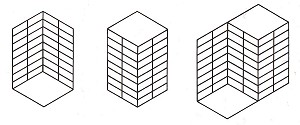
Figure 27, 28, 29
Strangely, Thiéry does not mention the second interpretation, but emphasizes that the figure bears similarities to Schroeder's steps (a drawing of the same steps which Prof. Schouten gave to Escher), and observes: "Here too, therefore, there exist two possible interpretations." He goes on to conclude that we may see the figure both as the prism of Figure 27 and as the prism of Figure 28, each with an extension.
It is a less well-known fact that the symmetrical Thiéry figure (fig. 26) can also be perceived as an entirely unambiguous figure. Professor J .B. Deregowski once brought me a wooden block having precisely such a form. For those who have seen such an object, Thiéry's figure ceases to be ambiguous. If you trace the figure's "construction plan" (fig. 30) onto another piece of paper, cut it out and make it up, you will see immediately how it works. Viewing your paper model from above, you will see the Thiéry figure; it will then be difficult for you ever again to see it as ambiguous. The EYE prefers simple solutions!
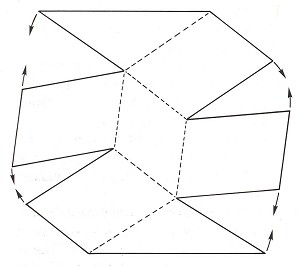
Figure 30. "Construction plan" of Thiéry's figure
When presented with geometrically ambiguous figures, the EYE spontaneously and alternately offers us two spatial solutions. Something is either concave or convex; we are either looking up at the underside or down onto the top of a surface... The obvious question here is whether it is possible to confront the EYE with a situation in which this alternate "either/or" becomes a simultaneous "both/and". This would produce an impossible object, since two interpretations cannot both be correct at the same time. In Chapter 4 we shall be meeting figures in which this extraordinary situation indeed arises.
